Section 3.3 = #3
Give a big-θ estimate for the number of operations of this algorithm:
m := 0
for i := 1 to n
for j := i +1 to n
m := max(aiaj, m)
The values of i and j:
i := 1 <= n     →   n (rounds)
j := i + 1 <= n   →   n – 1 (rounds)
i := n + 1 <= n  →  1 (Ends loop)
j := n + 1 <= n  →  1 (Ends loop)
n(n – 1) + 1 + 1 = n^2 – n + 2
Exactly n^2 – n + 2 comparisons are used whenever this algorithm is applied. Hence, the algorithm has time complexity θ(n^2).
Hi Brian. There’s an error in your calculation of the number of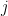
loops. Notice that 
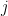goes from 
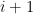to 
, not from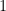 
to 
. Therefore, for different values of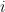 
there are different numbers of possible values of 
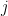. For example, if 
then 
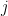can be 
, so there are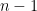 
values of 
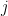. But if 
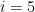then 
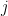can be 
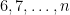, there are only 
values of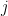 
. In particular, the 
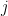loops are getting shorter as 
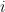gets higher. It might be easier to check the number of values of 
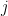for each individual value of 
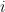, and then add them all up. Hint: your complexity is correct but your exact number of comparisons isn’t.