As soon as class ended today, I realized that we had forgotten something important when setting up the integral that computed the volume of the solid obtained by rotating the region between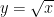 
and the 
-axis, between 
and 
, about the -axis using the method of cylindrical shells. I’ll review the set-up here, and add the part I forgot.
Since we’re rotating about a horizontal line (the -axis) and we’re going to use the method of cylindrical shells, that means we’ll integrate with respect to the vertical coordinate 
. So the first part of the set-up is to write:
.
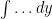This means that our integrand has to be given in terms of the variable . The integrand is the area of the infinitely thin cylindrical shell that you get from rotating a horizontal segment at height about the -axis:
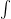(area of cylindrical shell) 
.
When you cut open this infinitely thin cylindrical shell, you just get a rectangle whose area is its length times its width. Its length is the circumference of the cylinder; its width is the length of that horizontal segment at height . The radius of the cylindrical shell is just the height of the horizontal segment at height , so the circumference of the cylindrical shell is 
. We can add this to our integral above:
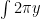*(length of horizontal segment) .
Now we just have to figure out the length of that horizontal segment at height . Since it’s horizontal, its length will just be the difference of the $x$-coordinates of its endpoints. The endpoint at the far right will be the same no matter what is. Here, the right-hand boundary of the region is the line , so the right endpoint of the horizontal segment has -coordinate 4. The left endpoint of the horizontal segment will depend on what is, but it will always be a point on the graph of 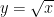. So the left endpoint of the horizontal segment at height is just . This means that the length of the horizontal segment at height is 
…but our integrand can’t have the variable in it…we’ve set it up so that we’re integrating with respect to . Since ,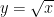 
. We just replace the we see in the formula for the length of the segment with 
. So the length of the horizontal segment at height is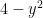 
:
.
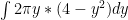This is the integral we set up in class. It will not compute the volume of the solid because it’s an indefinite integral and not a definite one. We forgot to add limits of integration. Remember that we’re integrating with respect to , which plays the role of the radius of the cylindrical shell. We know that goes from 0 to 2, and we know that 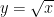, so this means that the radius goes from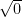 
to 
. This means that the definite integral that computes the volume is:
.
Here’s what I’d do to evaluate this integral:
![= 2 \pi (2y^2-\frac{1}{4}y^4)]_0^2](https://s0.wp.com/latex.php?latex=%3D+2+%5Cpi+%282y%5E2-%5Cfrac%7B1%7D%7B4%7Dy%5E4%29%5D_0%5E2&bg=ffffff&fg=000000&s=0 "= 2 \pi (2y^2-\frac{1}{4}y^4)]_0^2")
.
Therefore the volume is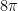 
.
