Category: Test #1 Review (Page 1 of 2)
WeBWorK
Functions – Inverse Functions: Problem 9
If f(x)=(2x-8)/(5x+4), find the inverse function.
First we interchange x and y:
x=(2y-8)/(5y+4)
Next, we multiply both sides by 5y+4:
x(5y+4)=2y-8
Distribute the x:
5xy+4x=2y-8
Rearrange the terms:
4x+8=2y-5xy
Factor out y:
4x+8=(2-5x)y
Divide both sides by (2-5x):
(4x+8)/(2-5x)=y
Replace y with f^-1(x):
f^-1(x)=(4x+8)/(2-5x)
Inspiration Question: Absolute Value Inequalities – Problem 7
State Answer in Interval Notation
Question: “|7x-3| ≥ 10”
First, we need to figure out the solution to the following equations to discover the endpoints of the interval(s):
7x -3 = 10 and -(7x-3) = 10
- 7x-3 = 10 —> 7x = 13 —> x = 13/7
- -(7x-3) = 10 —> -7x+3 = 10 —> -7x = 7 —> x = -1
Second, we need to test each interval created on the number line with test points that exists between each interval to see if the inteval makes a true statement.
The test points will be: -5, 0, 5.
- -5 tests the interval of (-inf, -1], the conclusion is … True Statement
- 0 tests the interval of [-1, 13/7], the conclusion is … False Statement
- 5 tests the interval of [13/7, inf), the conclusion is … True Statement
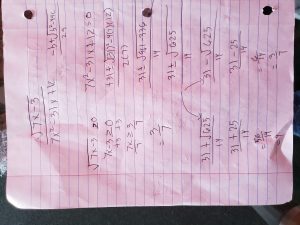
We disgard the any and all false statements as they are untrue (the work is below).
- |7x-3| ≥ 10 —> |7(-5)-3| ≥ 10 —> |-35-3| ≥ 10 —> |-38|≥ 10 —> 38 ≥ 10 = True Statement
- |7x-3| ≥ 10 —> |7(0)-3 | ≥ 10 —> |0-3| ≥ 10 —> |-3| ≥ 10 —> 3 ≥ 10 = False Statement
- |7x-3| ≥ 10 —> |7(5)-3| ≥ 10 —> |35-3| ≥ 10 —> |32| ≥ 10 —> 32 ≥ 10= True Statement
Thirdly, we must reiterate what whether or not the endpoints that we discovered in part 1 are, in fact, part of the solution set.
As shown in step 1, the interval endpoints ARE part of the solution set because the inequality is NOT strict.
The final part of the problem is writing our answer in interval notation:
Answer: (-inf, -1] U [13/7, inf)
And that’s that.
If you have any questions, or noticed any small or large mistakes with my work – please, comment and tell me what is wrong or what questions you might have with my method.
Thank you for reading, and have a nice day.






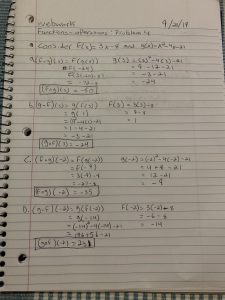

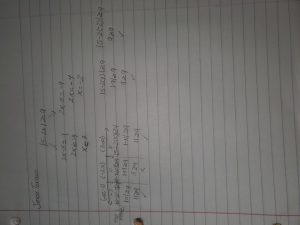






Recent Comments