Category: Examples & Explanations (Page 2 of 3)

A few people in class joined office hours earlier today and we discussed the following Rational Functions exercise (which I think we discussed in class also). I thought I would post some of what we discussed, as a summary of how to analyze rational functions.

Domain:

Recall that for the domain, we need to find the roots of the denominator, i.e., the x-values for which the denominator is 0. It’s clear (since we are given the polynomial in factored form) that the roots of the denominator are:

x = -12, x = 2, x = -10

This gives us the domain: all real numbers except for the roots of the denominator (since the rational function is undefined at those values!). This is (partially) shown in interval notation in the screenshot!

Vertical asymptotes:

Let’s look at the vertical asymptotes next, since that is related to the roots of the denominator used to find the domain: the roots of the denominator are possibly vertical asymptotes. In this example, the two vertical asymptotes are

x = 2, x = -10

Why isn’t the third value x = -12 a vertical asymptote? Note that the corresponding factor (x + 12) appears in the numerator as well as the denominator, and so we can simplify the function by cancelling that common factor. That means that x = -12 is not a vertical asymptote, and instead is actually the location of a hole.

(Why? Because we can see from the simplified form that

f(x) ≈ 3(x+4)² / [(x-2)(x+10)] for x ≈ -12

(where “≈” stands for “approximately equal to”)

meaning that the values of f(x) don’t “blow up” to ±∞ for input values close to x= -12.

Holes

So we have concluded the function has a single hole at x = -12. As you can see from the screenshot, we entered (-12, ??) into WebWork–this exercise requires that we find the y-coordinate of the hole.

How do we do that? We use the observation above, that

f(x) ≈ 3(x+4)² / [(x-2)(x+10)] for x ≈ -12

We can restate this as:

f(-12) ≈ 3(-12+4)² / [(-12-2)(-12+10)] = 3(64)/[(-14)(-2)] = 48/7

This gives us the y-coordinate of the hole, i.e. the hole is at

(-12, 48/7)

Horizontal asymptote

Recall that for a rational function where the numerator and denominator are polynomials of the same degree, we look at the ratio of the leading terms to identify the horizontal asymptote.

That is the case in this example, since both the numerator and denominator are cubic polynomials. In particular:

f(x) = (3x³ + ….) / (x³ + ….)

(You should understand why this is! Think about where the leading terms come from, if you were to start multiplying out the factored forms of the numerator and denominator.)

Hence, the ration of the leading terms is

y = 3x³/ x³ = 3

This is the equation of the horizontal asymptote!

Putting it all together in Desmos

As I have been emphasizing, it’s a good idea to use Desmos as you do these exercises. In this case, I created a graph of the original function, and added in the vertical and horizontal asymptotes, as well as the location of the hole and the single root (x-intercept):

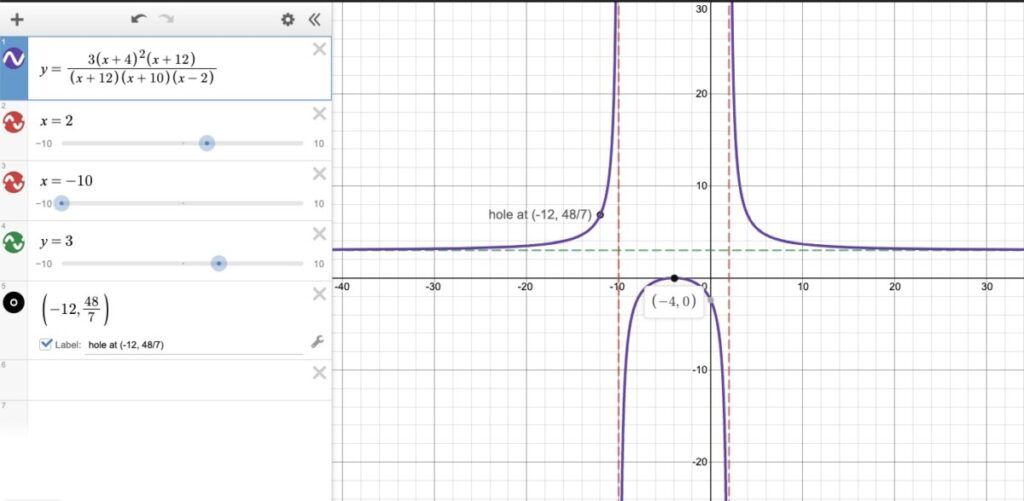
You can view this Desmos graph via https://www.desmos.com/calculator/b5ktqa5rai

If you would like to review the material that’s on Quiz #3, I recommend that you study Example 10.7 in the textbook–especially 10.7(a):

In this example, you are presented with various polynomials and asked to find the roots, and use them to factor the polynomial completely.

Let’s take a closer look at the polynomial in 10.7(a): the cubic polynomial
f(x) = 2x³ – 8x² – 6x + 36.

How do we find the roots of this cubic? As you can see in the textbook explanation, we can start by looking at the graph! Here’s a nicer version of the graph I created in Desmos:

Note that I factored the common factor of 2 out of the polynomial. That makes the algebra a little bit simpler going forward…

Now, as the textbook explains as well, from looking at the graph it seems like x = -2 and x = 3 are roots. But to be sure we should check algebraically, i.e., by evaluating f(-2) and f(3), as they do in the textbook. The algebra is (just a bit) simpler with the 2 factored out:

f(3) = 2*( 3^3 – 4*(3^2) – 3*3 + 18) = 2*(27 – 36 – 9 + 18) = 2*0 = 0

Now how can we use the roots to factor the polynomial? That’s where the “Factor Theorem” comes in. It’s stated in Sec 8.2 of the textbook (read that section!); here is a statement via wikipedia:

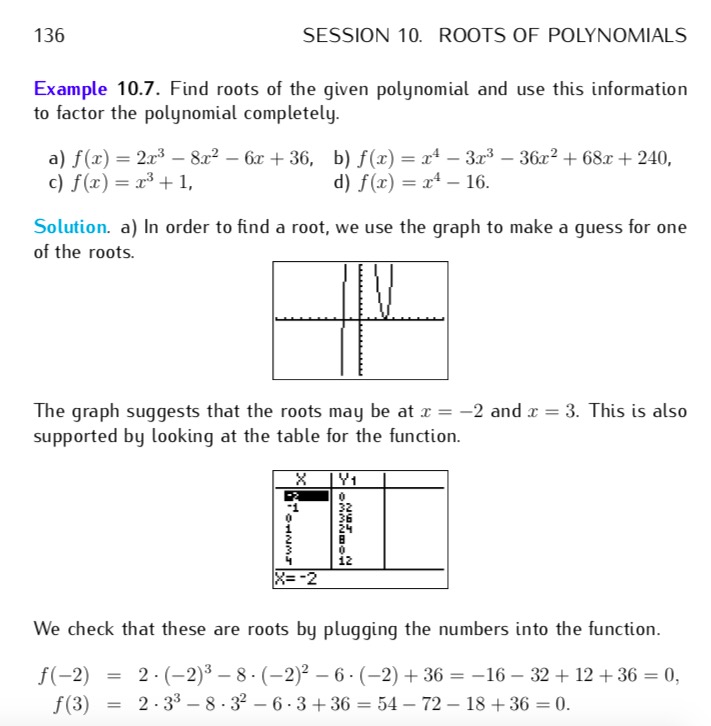
“The factor theorem states that a polynomial  has a factor  if and only if   (i.e.   is a root).”

Note that k here represents a constant value for the input variable x.

So in our example, since we know that k = 3 is a root of f(x), therefore we know that (x – 3) is a factor of f(x)! Similarly, since k = -2 is a root of f(x), we know that (x – (-2)) = (x + 2) is a factor of f(x).

How can we use that information to actually factor f(x)? By long division! In this case, we would set up long division in order to compute either

f(x) ÷ (x – 3)

or

f(x) ÷ (x + 2)

In the textbook (see the bottom of p136) they carry out the long division f(x) ÷ (x-3) to show that

f(x) = (x – 3)(2x² – 2x – 12)

Here’s the long division for (x³ – 4x² – 3x + 18) ÷ (x + 2) (I’m leaving out the factor of 2 from f(x) for the long division, but then put it back in at the bottom when factoring f(x)):

Therefore, we conclude that

f(x) = 2(x + 2)(x² – 6x + 9)

and in this case we can factor the quadratic to get:

f(x) = 2(x + 2)(x² – 6x + 9) = 2(x + 2)(x – 3)(x – 3) = 2(x + 2)(x – 3))²

This shows that the only roots of f(x) are x = -2 and x = 3 (where the latter is a root of multiplicity 2), and thus (as the Desmos graph seemed to show, but which we have now proved algebraically): the only x-intercepts of the graph are at (-2, 0) and (3,0).

Also note that we can easily find the y-intercept of the graph by computing f(0):

f(0) = 2*( 0^3 – 4*(0^2) – 0*3 + 18) = 2*(18) = 36

i.e., the y-intercept is at (0, 36), again as indicated by the Desmos graph.

I received a couple questions about the last exercise on the WebWork set “Functions – Operations” in which you are given two functions $f$ and $g$, and are asked to write down the compositions $(f \circ g)(x)$ and $(g \circ f)(x)$, and also write down their domains.

For example, let’s take

$ f(x) = \sqrt{44 – 5x} $ and $ g(x) = 5x^2 – 1 $

Then $(f \circ g)(x) = f(g(x)) = \sqrt{44 – 5(5x^2 – 1)} = \sqrt{49 – 25x^2}$

and hence to find the domain of $f \circ g$, we need to solve the inequality:

$49 – 25x^2 \geq 0$

$49 \geq 25x^2$

$x^2 \leq 49/25$

$- 7/5 \leq x \leq 7/5$

i.e., the domain is $ [ – 7/5 , 7/5 ] $.

Composing the functions in the opposite order:

$(g \circ f)(x) = g(f(x)) = 5(\sqrt{44 – 5x})^2 – 1 = 5(44-5x) – 1 = 219 – 25x$

Now it would seem that therefore the domain of $g \circ f$ is all real numbers, i.e., $(\infty, \infty)$, but this is incorrect, because it ignores that we simplified $(\sqrt{44 – 5x})^2$ to $44-5x$; the domain $(g \circ f)$ is actually restricted by the square root.

Another way of seeing this is to notice that, in order to calculate $(g \circ f)(x) = g(f(x))$ for a given input value of $x$, we first have to calculate $f(x) = \sqrt{44 – 5x}$ (and then we plug that value into $g$).

Hence, the domain of $(g \circ f)(x)$ is restricted to those inputs $x$ such that $44 – 5x \geq 0$, i.e., $ x \leq 44/5$.