The college is closed for spring break Monday April 22 thru Tuesday April 30, so our next class will be Wednesday May 1.
I have reopened a number of WebWork sets, so you can use this time to complete any WebWork exercises from the following sets that you didn’t do earlier in the semester:
- Expressions-Arithmetic-Integer Exponents
- Expressions-Polynomials-Linear Expressions
- Expressions-Polynomials-Multiply Polynomials
- Expressions-Polynomials-Evaluate Add Subtract Polynomials
- Expressions-Polynomials-Factor Trinomials
- Expressions-Polynomials-Factor Trinomials AC Method
- Expressions-Radical Expressions-Adding and Subtracting
- Expressions-Radical Expressions-Multiplying
- Expressions-Radical Expressions-Simplifying
- Expressions-Rational Expressions-Adding and Subtracting Part 1
- Expressions-Rational Expressions-Complex Fractions 1
- Equations-Quadratic Equations-Quadratic Formula
I will also be opening some WebWork sets on trigonometry over te break so that you can get started on that topic, which we will discuss when we get back.
We will have only 3 weeks left in the semester after we come back from spring break–the final exam will be on Wednesday May 22.
We will also have a third midterm exam in the week before the final, which will cover trigonometry plus some topics from earlier in the semester (as review for the final).




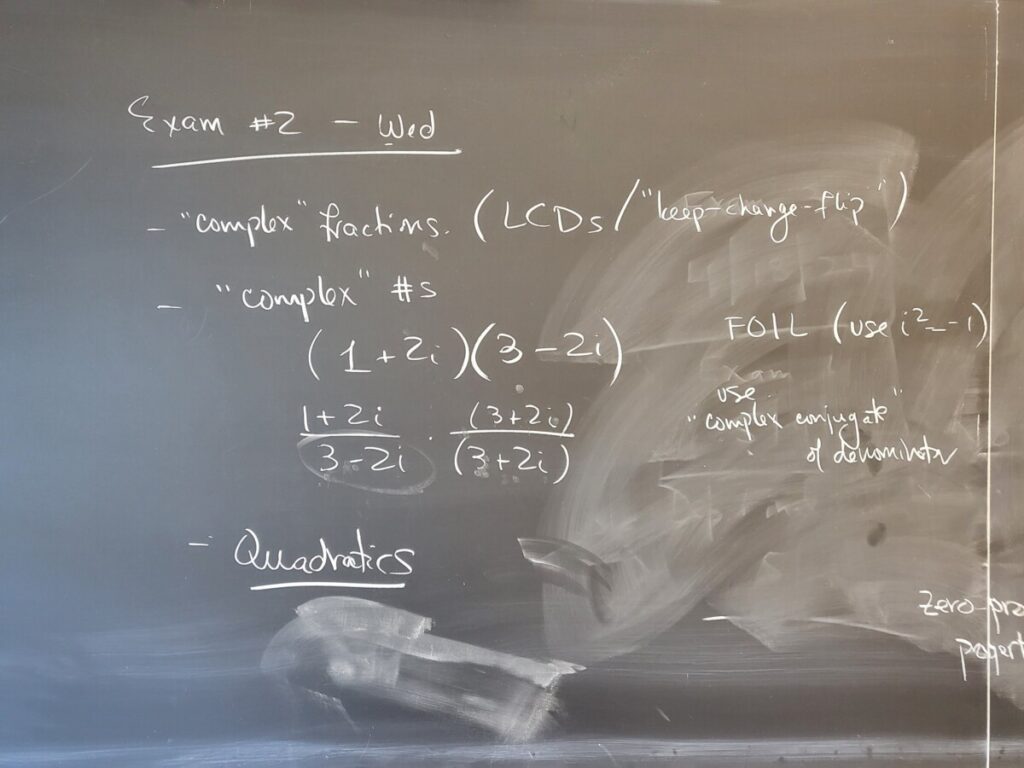

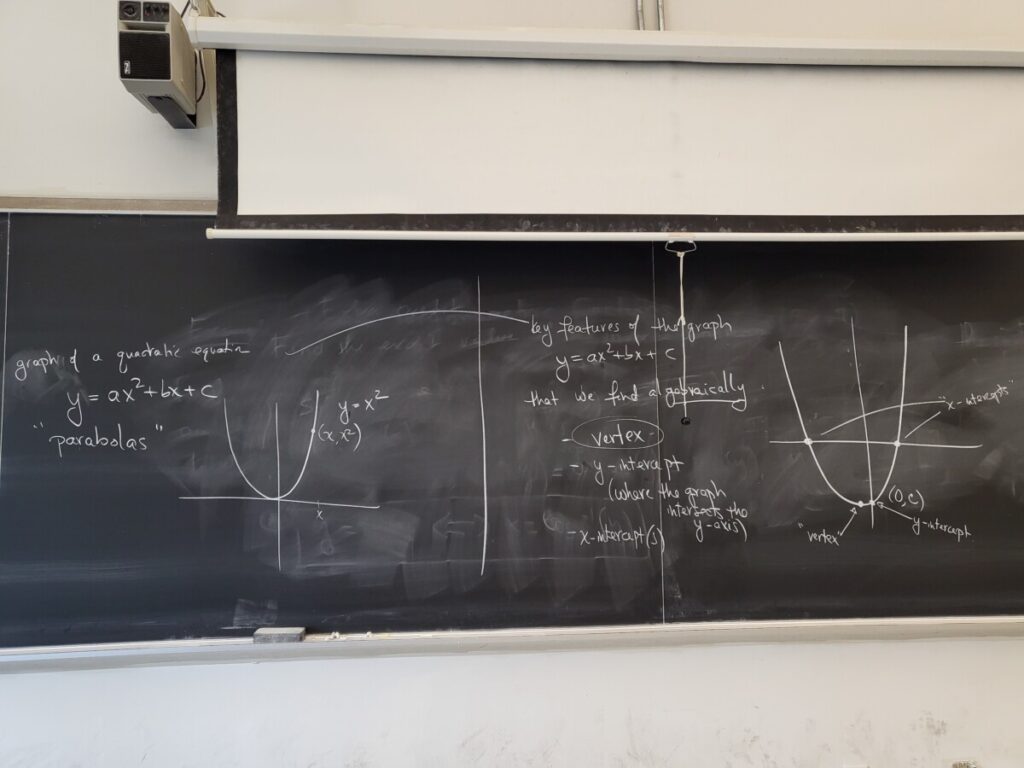

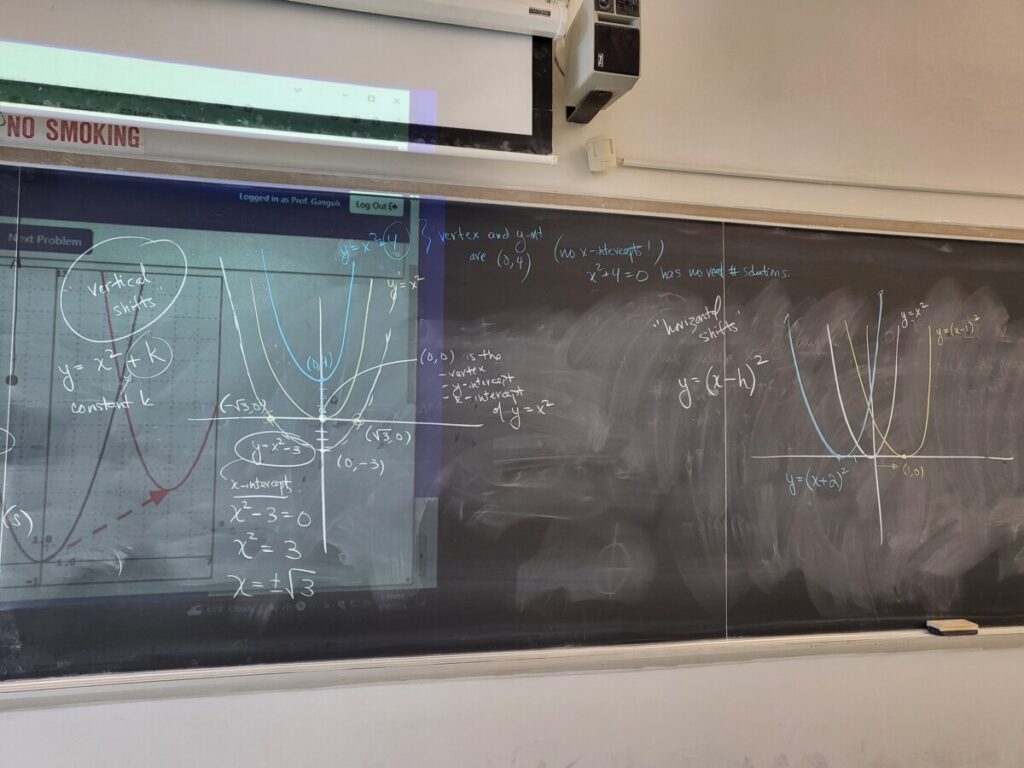
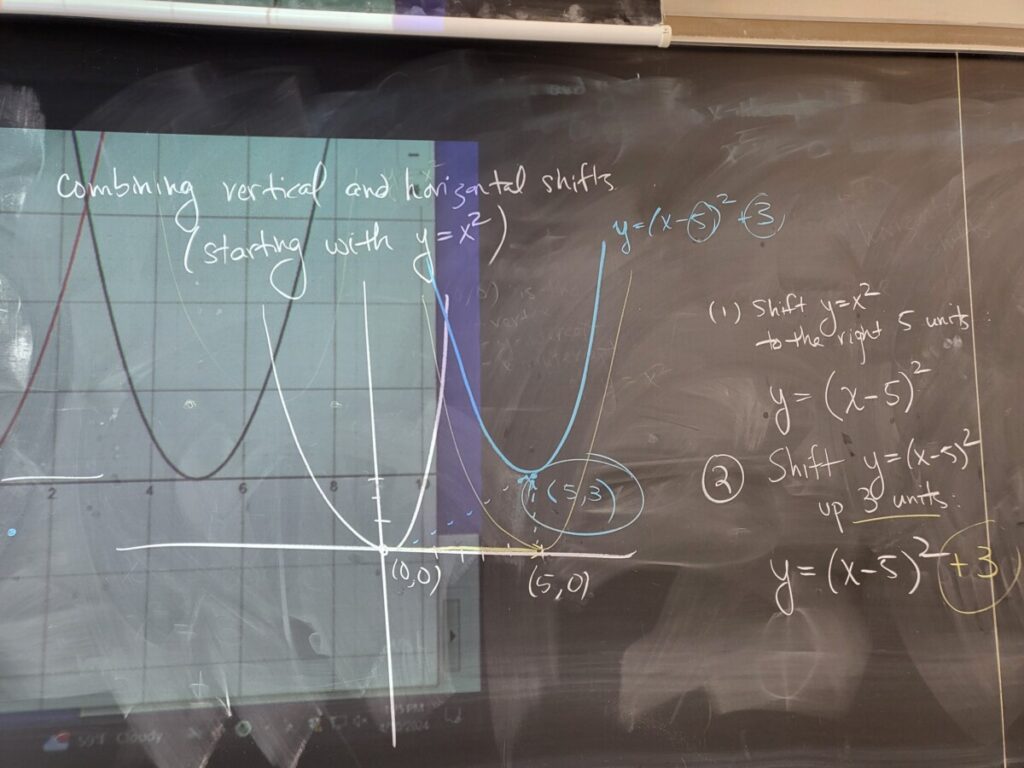





Recent Comments