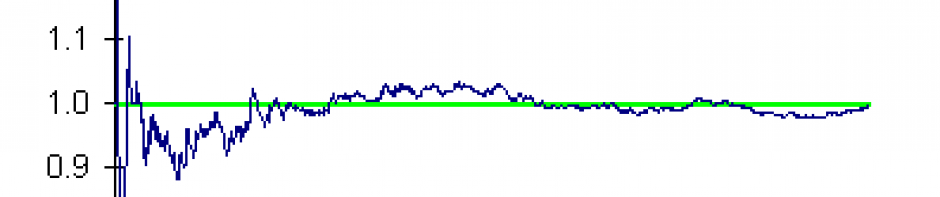
In the site header, you are seeing a demonstration of the Law of Large Numbers, the fundamental theorem for statistics. Perform a random action which has an expectation or average of about 1, such as flipping two coins and counting the number of heads. Repeat this action over and over again. Each time the action is performed, we recalculate the average. As the number of repetitions increases, the likelihood that we will be located close to the horizontal line y=1 increases. More precisely, if we quadruple the number of repetitions, we will half the average distance we are from that line.
Remember that participating on the openlab is part of your grade. Start by becoming a member of the site.



Hi, this is a comment.
You as students are encouraged to make them!
On average 64 % of Finite Mathematics students spend some time in the Mathematics Department’s resource room. Half of these students spend more than 90 minutes per week in the resource room. At the end of the semester the students in the class were asked how many minutes per week they spent in the resource room and whether they passed or failed. The passing rates are summarized in the following table:
Time spent in resource room Pass %
None 27
Between 1 and 90 minutes 42
More than 90 minutes 81
If a randomly chosen student did not pass the course, what is the probability that he or she did not study in the resource room?
I am really confused anyone have any ideas