Fibonacci type proportions
Type sizes series you could use for balance with sense of proportion

Fibonacci
https://en.wikipedia.org/wiki/Fibonacci_number

A series of numbers with the pattern of each number being the sum of the previous two.
The sequence:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…

Fibonacci type proportions
Type sizes series you could use for balance with sense of proportion
5 • 8 • 13 • 21 • 34 • 55 • 89 …
6 • 10 • 16 • 26 • 42 • 68 • 110 ……

In mathematics, the Fibonacci numbers are the numbers in the following integer sequence, called the Fibonacci sequence, and characterized by the fact that every number after the first two is the sum of the two preceding ones:

1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , … 

Often, especially in modern usage, the sequence is extended by one more initial term:

0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , …} .

https://3.7designs.co/blog/2010/10/how-to-design-using-the-fibonacci-sequence/

 Type Proportion Tool Online

illustrate how these systems were used.

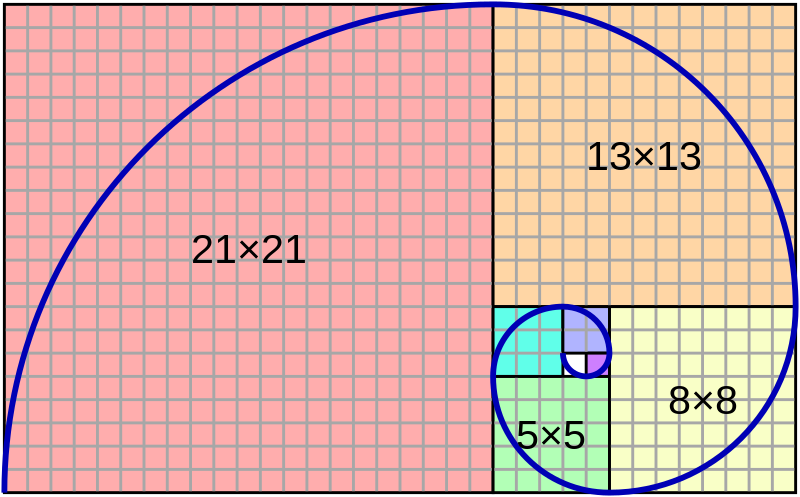
"Fibonacci number" by wikipedia.org is licensed under CC BY-SA 4.0

"Canons of page construction" by wikipedia.org is licensed under CC BY-SA 4.0