Probability is a measure that is associated with how certain we are of the outcomes of a particular experiment or activity. An experiment is a planned operation carried out under controlled conditions.
Today: Overview, Conditional Probability, Independence, Multiplication Rule
Helpful model:
- Draw a picture (box, circle, etc) – this is everything that ‘could happen’.
Terminology:
- Individual points in the picture are outcomes – the result of one experiment. Possibilities.
- The whole picture (all outcomes) is called the sample space. List of all the possibilities.
- An event is a group of one or more outcomes.
- The probability of an event is the ratio $\frac{\text{size of event}}{\text{size of sample space}}$. “How much of the total sample space does our event make up?”
Examples of Experiments
Roll a die.
Choose one person from the class.
A couple is having a baby.
For each example above, what’s the experiment? What are the outcomes? What are some ideas of different events that we might consider? Hint: You can often come up with an event by making up a question like “what is the probability that blah” — the blah is an event.
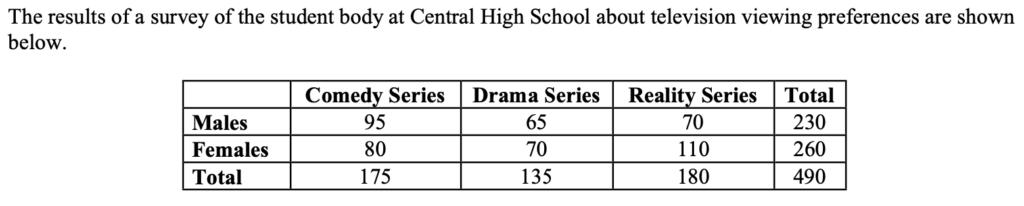
Example. What is the probability of each event? (Find the size of each event, then divide by total possible to find the probability).
- Female $P(F)$
- Prefers Drama series $P(D)$
- Doesn’t prefer Reality series $P(R’)$ (note: $R’$ means “$R$ complement”)
- Prefers Reality series $P(R)$
- Question: What’s the connection between the probability of an event and the probability of its complement?
- Female AND Prefers Drama (AND = falls in both events) $P(F \cap D)$
- Female OR Prefers Drama (OR = falls in one event or the other or both) $P(F \cup D)$
Conditional probability
Definition: Conditional Probability. $P(A|B)$ means the Probability of A, given B. We think of this as shrinking sample space to only the event B, and asking “how likely is A to occur, within B?” $$P(A|B)=\frac{P(A\cap B)}{P(B)}$$
Example cont’d – Working with given information (conditional probability). Use the data from Example 1 to find each probability.
- What is probability that a student prefers Reality Series, given that they are Female $P(R|F)$? That is, if I tell you the chosen student was Female, now what is the probability that they prefer Reality series? Is this the same as the probability $P(R)$ that a student prefers Reality Series (with no information given about their gender)?
- What is the probability that student is Male, given that they like Drama Series?
- What is the probability that a randomly selected Female student likes Drama Series?
- What is the probability that a student is both Male and likes Comedy series, if they are selected randomly from all students who are either Male or who like Comedy Series?
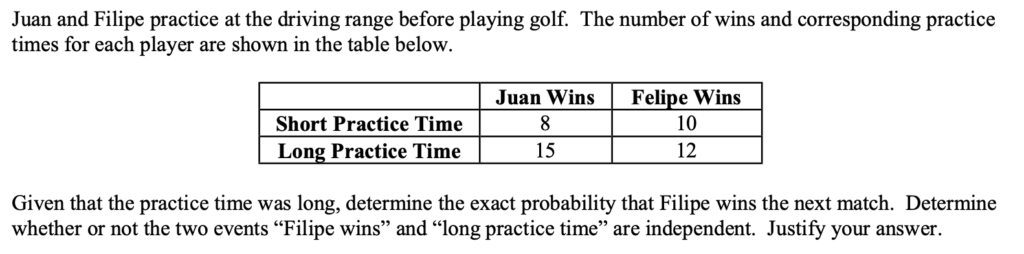
Independent Events
What does independent mean in discussions about probability?
Two events are independent if knowing one of them occurred does not affect the probability that the other occurred. Technically, this means:
Defn. Two events $A$ and $B$ are independent if $P(A) = P(A|B)$.
Equivalently, if $P(B)=P(B|A)$.
Example.
On a rainy afternoon in July 2023, you go to a NYC movie theater and hang out in the lobby. A moviegoer is selected at random. Are you willing to bet $1 that the person has seen the Barbie movie?
It turns out your friend is also hanging out in the lobby, and they have actually interviewed 20 moviegoers in the previous hour. 16 out of those 20 moviegoers had seen the Barbie movie. Does this change your answer?
What if the person has seen Oppenheimer?
Turns out, of those 20 moviegoers, 5 had seen Oppenheimer. 1 moviegoer had seen both Barbie and Oppenheimer. Does knowing that the selected person had seen Oppenheimer change your answer?
What if the person is a fan of the Indigo Girls?
Turns out, of the 20 original moviegoers, 15 of them are fans of the Indigo Girls. 12 of them are both fans of the Indigo Girls and had also seen the Barbie movie. Does knowing that the moviegoer is a fan of the Indigo Girls change your answer?
Multiplication Rule
Multiplication Rule. The probability that both $A$ and $B$ occur is equal to the probability that one event occurs, times the probability that the other event occurs given that the first event occurred. $P(A\cap B)=P(B)\cdot P(A|B)$
IF $A$ and $B$ are independent, then $P(A\cap B)=P(B)\cdot P(A)$
Resources on Probability and Statistics
- The Bear in Moonlight – Math With Bad Drawings’ 7-part series on probability (disguised in story form)
- OpenLab course hub for MAT 1372 (Probability and Statistics)
- Introduction to Probability from OpenStax textbook on Probability
- Adjustable spinner (change # of categories and probability of each, then simulate spins)

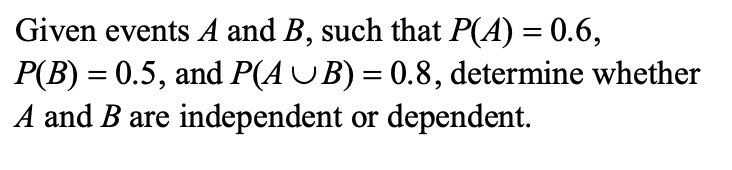




0 Comments
1 Pingback