Why do we care so much about triangles? Why don’t we have something like “trigonometric functions” for other shapes, like rectangles, pentagons, etc?
Furthermore, why does trigonometry focus on right triangles? What about other kinds of triangles?
Discuss:
- Triangulation: any shape with straight sides can be divided into triangles.
- The relationship between distance/direction and coordinate axes. (also: Pythagorean Theorem, distance formula. Also: any triangle can be decomposed into two right triangles.)
Trigonometry in Right Triangles
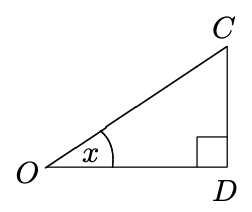
Defn. Suppose $x$ is in the open interval $(0,90)$, i.e., for $0<x<90$. Take any right triangle $\triangle O C D$ so that its acute angle at the vertex $O$ has $x$ degrees and so that $O C$ is the hypotenuse. Then $\angle D$ is the right angle, as shown:
By definition,
$$\sin x =\frac{|C D|}{|C O|}\left(=\frac{\text { opposite side }}{\text { hypotenuse }}\right)$$
$$\cos x =\frac{|O D|}{|C O|}\left(=\frac{\text { adjacent side }}{\text { hypotenuse }}\right)$$
$$\tan x =\frac{|C D|}{|O D|}\left(=\frac{\text { opposite side }}{\text { adjacent side }}\right)$$
Question: What are definitions of $\sec x$, $\csc x$ and $\cot x$?
What about angles bigger than $90$ or less than $0$?
Trigonometry in the Unit Circle
Defn. Suppose $t$ is any real number, and let $P_t$ be the image of the point $(1,0)$ after a clockwise rotation about the origin of $t$ degrees. Then the $x$-coordinate of $P_t$ is $\cos t$ and the $y$-coordinate of $P_t$ is $\sin t$.
- Is $P_t$ a point on the unit circle? How do we know?
- How do we justify the move from right triangles to the unit circle? If $t$ is in the open interval $(0,90)$, does the “right triangle” definition of sine and cosine agree with the “unit circle” definition?
Expressions, Equations, and Identities
Question. What is the difference between an expression and an equation?
Discussion:
- An equation has an equals sign, an expression does not.
- An expression is like a function – put in a value, it will give you back a value.
- An equation is like a “True/False” machine – put in a value, it will tell you True or False.
What is the difference between an equation and an identity?
Definition. An equation $f(x)=g(x)$ in one variable $x$ is a question that asks whether there are any numbers that make the sides equal, that is, numbers $k$ so that $f(k)=g(k)$.
Definition. An identity $f(x)=g(x)$ is an equation which is true for all values of the variable (sometimes we allow a limited number of exceptions, for example values of $x$ for which one or both sides of the equation is undefined).
Example. For each equation, is it an identity?
- $2x+6=8x$
- $(x-4)^2+8x=x^2+4^2$
- $(x-4)^2=-9x+22$
- $x-\frac{\log_4 (e^x)}{2\log_4 \sqrt{e}}=0$
Example. For each equation, is it an identity?
- $2\cos x = 1$
- $(\sin x)^2+(\cos x)^2=1$
- $(\tan x)^2 + 1 = (\sec x)^2$
- $1-\cos x=\frac{\sin ^{2} x}{1+\cos x}$
- $\sin x + \cos x =1$
What do we do with equations, versus with identities?
To solve an equation means to obtain all the solutions of the equations.
- This can be done by starting with the given equation and applying a series of algebra steps, each preserving equality, until the solution or solutions are obtained.
- Sometimes, we draw a diagram, rely on a definition, or use a graphing calculator or other technology to help us.
To prove an identity, we must establish that it is true for any value of $x$.
- This can be done by starting with one side and applying a series of algebra steps, each preserving the value of the expression, to obtain the other side.
- It can also be done by starting with a known identity or definition and applying a series of algebra steps, each preserving equality, to obtain the desired identity.
- Finally, one can also be start with the given identity and apply a series of algebra steps until a known identity is obtained, as long as each step is reversible.
Example. For each equation in the previous example:
- If the equation is not an identity, find all the solutions $x$ in the interval $[0,360]$.
- If the equation is an identity, prove the identity.



0 Comments
3 Pingbacks