Probability

Probability is a measure that is associated with how certain we are of the outcomes of a particular experiment or activity. An experiment is a planned operation carried out under controlled conditions.

Today: Overview, Conditional Probability, Independence, Multiplication Rule

Helpful model:

• Draw a picture (box, circle, etc) – this is everything that ‘could happen’.

Terminology:

• Individual points in the picture are outcomes – the result of one experiment. Possibilities.
• The whole picture (all outcomes) is called the sample space. List of all the possibilities.
• An event is a group of one or more outcomes.
• The probability of an event is the ratio $\frac{\text{size of event}}{\text{size of sample space}}$. “How much of the total sample space does our event make up?”

For each example above, what’s the experiment? What are the outcomes? What are some ideas of different events that we might consider? Hint: You can often come up with an event by making up a question like “what is the probability that blah” — the blah is an event.

Example:

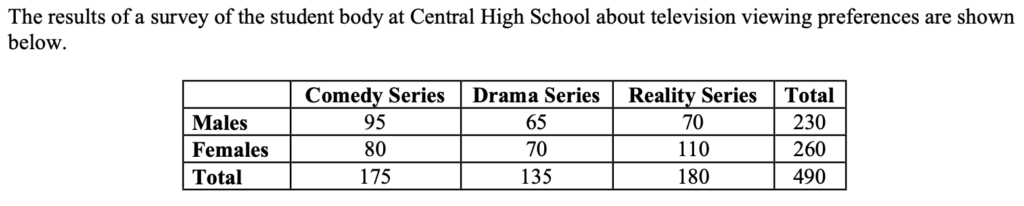
What is the experiment? Choose a student at random.

What is the probability of each event? (Find the size of each event, then divide by total possible to find the probability). The student chosen…

• Female $P(F)$
• Prefers Drama series $P(D)$
• Doesn’t prefer Reality series $P(R’)$ (note: $R’$ means “$R$ complement”)
• Prefers Reality series $P(R)$
  • Question: What’s the connection between the probability of an event and the probability of its complement?

Combining Events

• Female AND Prefers Drama (AND = falls in both events) $P(F \cap D)$
• Female OR Prefers Drama (OR = falls in one event or the other or both) $P(F \cup D)$

Working with given information (conditional probability)

• What is the probability a student prefers Reality Series?
• What if I tell you the chosen student was Female, now what is the probability that they prefer Reality series?

Conditional Probability. $P(A|B)$ means the Probability of A, given B. We think of this as shrinking sample space to only the event B, and asking “how likely is A to occur, within B?” $$P(A|B)=\frac{P(A\cap B}{P(B)}$$

What does independent mean?

Two events are independent if knowing one of them occurred does not affect the probability that the other occurred.

Defn. Two events $A$ and $B$ are independent if $P(A) = P(A|B)$.
Equivalently, if $P(B)=P(B|A)$.

• Back to Example 1: Are the events “Female” and “Prefers Drama” independent?

Multiplication Rule. The probability that both $A$ and $B$ occur is equal to the probability that one event occurs, times the probability that the other event occurs given that the first event occurred. $P(A\cap B)=P(B)\cdot P(A|B)$
IF $A$ and $B$ are independent, then $P(A\cap B)=P(B)\cdot P(A)$