Complex Numbers

The algebraic perspective

“Give me a square root of -1”

We start with the real numbers $\mathbb{R}$.

We ask: What would happen if $x^2=-1$ had a solution?

We call that solution $i$. By closing under the operations of plus and times, we obtain the complex numbers.

Definition. The complex numbers are all numbers of the form $a+bi$, where $a$ and $b$ are real numbers and $i$ is a constant satisfying $i^2=-1$.

• Addition: If $a+bi$ and $c+di$ are complex numbers, then $(a+bi)+(c+di) = (a+c) + (b+d)i$ (we add like terms).
• Multiplication: If $a+bi$ and $c+di$ are complex numbers, then $(a+bi)\cdot (c+di) = (ac-bd)+(ad+bc)i$ (distribute, use the fact that $i^2=-1$, and collect like terms).

The geometric perspective

“Show me how to multiply points in the plane”

We start with the coordinate plane $\mathbb{R}^2$, consisting of ordered pairs of real numbers $(x,y)$. When we look at a point, we will also consider its size or modulus and its angle (formed with the positive $x$-axis).

If we want to treat points in the plane like numbers on the number line, we need to find a way to add them and multiply them. To define addition of two points, we can think of adding vectors (as in the image below). This exactly corresponds to “adding coordinate-by-coordinate”.

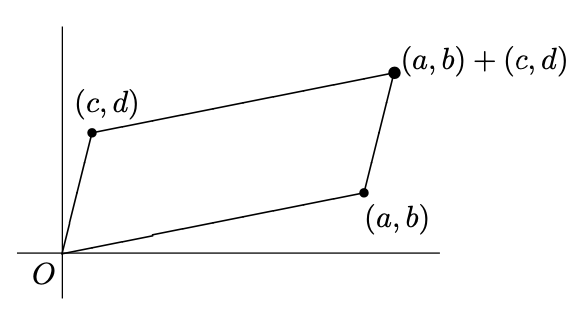
• Addition. To add two points $(a,b)$ and $(c,d)$, we add their corresponding coordinates $(a,b) + (c,d) = (a+c, b+d)$

To multiply two points, we will multiply lengths and add angles.

• Multiplication. To multiply two points $(a,b)$ and $(c,d)$, we find the point $(p,q)$ such that the length of $(p,q)$ is the product of the lengths of $(a,b)$ and $(c,d)$, and the angle of $(p,q)$ is the sum of the angles of $(a,b)$ and $(c,d)$
• Shocking fact: $(a,b)\cdot (c,d) = (ac-bd, ad+bc)$