One of the strongest results from our OpenLab #2 Survey was a request for more examples & problems in class. As you know, our class time is quite limited – so to take maximum advantage of the time we have, we are going to try an experiment. This OpenLab assignment, to be completed over the Spring Break, will ask you to get a head start on upcoming material by watching a few videos on the material. This will hopefully free up some class time for more examples & problems.
Assignment (Due Thursday, April 24, at start of class). Watch the videos below. You MUST watch the videos marked “required”. You CAN also watch the videos marked “optional,” – if you have any questions about today’s lecture, or if you need a reminder of how to do Partial Fractions, you should watch the appropriate videos here. Test your understanding by completing this problem:
Example. Find the Inverse Laplace Transform of :
SOLUTION:
Partial fraction decomposition:
Inverse Laplace Transform:
Then respond to the following prompts.
- What is one thing you learned from (any) one of the videos? What is one thing that you didn’t understand, or found confusing?
- Any questions about the example above?
- Any comment on this assignment? (helpful, confusing, useful, irritating, etc – what did you think of it?)
Extra Credit. You can earn extra credit by making up a problem and posting it here (do NOT post the solution yourself – let other people solve it!), or by giving a solution to someone else’s posted problem. Simple problems are fine – it can be much simpler than my example above. It should be one of the following types of problems:
- Finding the Laplace Transform (like we did today)
- Finding the Inverse Laplace Transform, or
- Partial Fractions
How do I type math formulas on the OpenLab? You can always type mathematical formulas just as you would type them into a TI-83 calculator, for example “sin(2t)+e^x”. But if you want them to look pretty (like this: 
VIDEOS – REQUIRED
- Overview: How do we use the Laplace Transform to solve differential equations? 2 min. https://www.youtube.com/watch?v=Z_wQvCyKjwE
- The Inverse Laplace Transform. 6 min. https://www.youtube.com/watch?v=Y8GXpS31CGI
NOTE: The first minute and a half is a more abstract discussion – follow it as best you can. BUT hold on for the example, which starts at 1:25. - (This is not required, but if you like these videos, he has a whole playlist of videos on the Laplace Transform here: https://www.youtube.com/playlist?list=PL5750E3CE53DB625A )
VIDEOS – OPTIONAL
- Finding the Laplace Transform of a Function: 3 min. This is a useful example of what we did in class today – it will also help you with WeBWorK 14.
http://youtu.be/ES2Lwzrw_UE - Partial Fraction Decomposition – a basic example. This is a good basic example.
https://www.youtube.com/watch?v=HZTv4zCgEnA - Partial Fraction Decomposition – another example. This is a slightly longer example, and it includes a good explanation of how to set up your partial fractions for different kinds of factors in the denominator.
https://www.youtube.com/watch?v=pZ9FfGy3Cfw
1. What is one thing you learned from (any) one of the videos? What is one thing that you didn’t understand, or found confusing?
I learned how to do inverse Laplace Transform from the video, and the partial fraction video refreshed my memory.
2. Any questions about the example above?
I try to use partial fraction to solve it and I get something, but I don’t know if it is the right answer.
3. Any comment on this assignment? (helpful, confusing, useful, irritating, etc – what did you think of it?)
This assignment is very helpful to me since both of the required and optional videos are very clear and straightforward in explaining.
Extra Credit – Finding the Laplace Transform
Ex. e^t*sin(5t)
1.What is one thing you learned from (any) one of the videos? What is one thing you didn’t understand, or found confusing?
I learned about the inverse laplace transform. The example the 2nd video confused me for a bit when he factored out the numerator.
2.Any questions about the example above?
Not sure if I did the partial fraction correctly
3. Any comment on this assignment?(helpful, confusing, useful, irritating, etc- what did you think of it?)
These videos were helpful with the examples he put in the video.
1. What is one thing you learned from (any) one of the videos? What is one thing that you didn’t understand, or found confusing?
I learned that the inverse Laplace can be easy, however manipulating it to use the table can be tricky. I’m still confuse about how to find the Laplace function of a differential equation.
2. Any questions about the example above?
Not sure if it is correct, Finding A and B was the most troubling part. How exactly using partial fraction will help us get to the Laplace function
3. Any comment on this assignment? (helpful, confusing, useful, irritating, etc – what did you think of it?)
It was really helpful, I think that having a lecture plus these videos could help one to better understand the topic if there still is any confusion,
1. What is one thing you learned from (any) one of the videos? What is one thing that you didn’t understand, or found confusing?
I’ve been watching Patrick JMT since calculus so I am used to his style of teaching and find it to be rather clear. Also I believe that his approach appeals to me more than that of Khan from Khan Academy.
2. Any questions about the example above?
The inverse Laplace transforms get very hairy when it’s not strictly following the format of the table. Therefore the example above is sort of tricky considering it has to be broken up, I definitely need practice.
3. Any comment on this assignment? (helpful, confusing, useful, irritating, etc – what did you think of it?)
Watching Videos is a great way to learn considering the added benefit of being able to re-watch a tricky section. Of course the con to videos instead of in class sessions is that you don’t have access to quick answers about the problems being performed; and also not being able to find an example that would closely resemble the assigned problem is really time consuming and irritating.
Extra Credit:
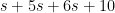
Find the Inverse Laplace Transform :
I entered the extra credit prob wrong here it is again:
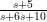
the ininverse laplace transform of
=cos3t+3
the inverse laplace transform of :
=cos3t+3
the video were helpful and easy to follow. once I refreshed my memory of partial fractions the above example was also manageable. The calculus part of the problem had me stumped for a bit but the concept was understood.
I found the assignment to be very helpful but a bit time consuming. I liked overall and would mind if we continued doing this.
Any comment on this assignment? (helpful, confusing, useful, irritating, etc – what did you think of it?)
1. I learned that sometimes you must manipulate the equation in order to get the Laplace transform and to get the inverse Laplace transform.
2. Is partial fraction expansion used to solve this example “manipulation stated above”.
3. The assignment was useful, but only for studying. Not helpful for lectures, I prefer in class lecture over “online”.
1. with the videos i was able to learn how to solve the partial fraction when the denominator can not be factor. a perfect example will finding the partial fraction of $latex\frac{2x^2+36}{x^3+2x^2+5x}$ where $latex{x^2+2x+5}$ is not factorable
2. proving the second derivative of the Laplace transform was a little challenging to understand
3. i think this assignment was very helpful and we should be given more options like these plus the class lecture to grab clearly the concept in this course
4. an example of problem is to find the inverse laplace of $latex\frac{s}{(s+1)(s^2+4)}$
1. with the videos i was able to learn how to solve the partial fraction when the denominator can not be factor. a perfect example will finding the partial fraction of: $latex\frac{2x^2+36}{x^3+2x^2+5x}$ where :$latex{x^2+2x+5}$ is not factorable
2. proving the second derivative of the Laplace transform was a little challenging to understand
3. i think this assignment was very helpful and we should be given more options like these plus the class lecture to grab clearly the concept in this course
4. an example of problem is to find the inverse laplace of :$latex\frac{s}{(s+1)(s^2+4)}$
$latex\frac{s}{(s+1)(s^2+4)}$
1. with the videos i was able to learn how to solve the partial fraction when the denominator can not be factor. a perfect example will finding the partial fraction of: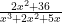
where :
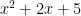is not factorable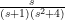
2. proving the second derivative of the Laplace transform was a little challenging to understand
3. i think this assignment was very helpful and we should be given more options like these plus the class lecture to grab clearly the concept in this course
4. an example of problem is to find the inverse laplace of :
4. the inverse Laplace transform of :$latex\frac{4s^2+27}{(s(s^2+9))}$ =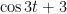
the inverse Laplace transform of :
=
(1)What is one thing you learned from (any) one of the videos? What is one thing that you didn’t understand, or found confusing?
– What i learned from the videos is that in order to find the inverse Laplace transform of a function we have to manipulate it by using a technique like partial fractions and then using the chart or table to find a similar function and use that to solve for our inverse.We can also check if its right by doing the reciprocal to see if it matches, both ways we have to use the chart and see if the functions match in order for us to solve for the inverse
(2) Any questions about the example above?
– I tried solving for the inverse but I’m not sure if its correct because when i trie finding the Laplace transform of my inverse i keep getting something different maybe I’m doing something wrong
(3) Any comment on this assignment? (helpful, confusing, useful, irritating, etc – what did you think of it?)
– This assignment o me was helpful because it forces us to understand the concept and it makes sure that we know exactly the steps to solvin these types of problems.
Extra credit:
Find the inverse Laplace transform of (s+5) / (s^2+6s+10)?
1. What is one thing you learned from (any) one of the videos? What is one thing that you didn’t understand, or found confusing?
One thing i learned from the videos is, to do the inverse Laplace transform you can use partial fractions to solve the problem however, its still a bit confusing on how to set up a partial fraction for different kinds of factors in the denominator.
2. Any questions about the example above?
Much different from doing the inverse with the table. Still a bit confused on how to apply partial fractions
3. Any comment on this assignment? (helpful, confusing, useful, irritating, etc – what did you think of it?)
I think its helpful to have extra assignments and videos for a better understanding
Extra credit:
Find the inverse Laplace transform
\frac{s-3}{(s-3)^2 +25}
(s-3)/((s-3)^2 + 25)
The thing I learned from watching the above videos is how the laplace table is related to given functions as well as how the bounds for “s” are determined when having a laplace transform with linearity. One thing I found confusing is how to breakdown given functions that needed to be turned into transforms with linearity especially with three factors (because of the s^2). After a while I got used to it though.
My question for the above problem is that is there another way of finding the laplace transform like factoring numerator/denominator and then factoring those terms, will this result in the same laplace transform?
The above problem took me quite some time, much more time than it took to do the webwork assignment, possibly because of the partial fractions required.
1. I learned Inverse Laplace Transform from the required videos. I still need a bit more practice on partial fractions.
2. I am not sure if my answer is correct.
3. The assignment was helpful the videos were clear and easy to understand.
Extra Credit
e^3t cos(4t)
1.What is one thing you learned from (any) one of the videos? What is one thing that you didn’t understand, or found confusing?
I learned inverse Laplace transform. the videos where clear and nothing was confusing.
2.Any questions about the example above?
no, very easy and strait forward example.
3.Any comment on this assignment? (helpful, confusing, useful, irritating, etc – what did you think of it?)
it was helpful, but in my opinion it is better to take the lecture in class and then do examples at home because we are used to that and also I am used to prof Reitz style in explaining even though the videos where clear and as we know every professor has his/her own method in teaching so sometimes it makes students confused to listen to others prof lectures because each one explains differently.
1. What is one thing you learned from (any) one of the videos? What is one thing that you didn’t understand, or found confusing?
I learned you’re able to solve a differential equation by using the Laplace transform.
2. Any questions about the example above?
Its a bit tricky when taking partial fractions.
3. Any comment on this assignment? (helpful, confusing, useful, irritating, etc – what did you think of it?)
Very helpful, although it seems that finding the correct way to use partial fraction can become difficult if the equation for taking the Inverse Laplace Transform is complicated.
Extra Credit:
Find the Laplace Transform
f(t)=9cos(900t)
1. What is one thing you learned from (any) one of the videos? What is one thing that you didn’t understand, or found confusing?
I have seen some Patrick jmt videos in the past and I like his way of teaching. With this video I learned how to do a laplace transform and that it is extremely time saving and easier to usea chart. For sure more practice will be needed before it becomes second nature.
2. Any questions about the example above?
Luckily after doing the WEBwork i was able to see some patterns with laplace transforms, when an equation looks as complicated as the one above; its best to try and split it using the available chart template.
3. Any comment on this assignment? (helpful, confusing, useful, irritating, etc – what did you think of it?)
I enjoy watching the videos online it does cutback on time to leave more room for practice, but of course the downside is not being able to get fast answers and the fundamentals of a subject might not be conveyed well enough in videos. But i think this could be a superior way to going about the class, and is definitely worth the experiment.
Extra Credit problem.
f(t)=6e^-5t +cos(10t)-9
1.What is one thing you learned from (any) one of the videos? What is one thing that you didn’t understand, or found confusing?
1. In the first video he showed us an overview of how using Laplace Transforms helps you solve differential equations, and the second video helped me better understand how to find the inverse Laplace transform of a function by using partial fractions and the table to find a similar function in order to solve for the inverse.
2. Any questions about the example above?
2. Not really, the example was pretty simple.
3.Any comment on this assignment? (helpful, confusing, useful, irritating, etc – what did you think of it?)
3. This assignment was helpful. This guy explained everything very clearly, so I had no problems understanding how to do the example above and the one in the video.
1. What is one thing you learned from (any) one of the videos? What is one thing you didn’t understand, or found confusing?
I learned how to do the Inverse Laplace Transform, as well a better understanding of Laplace Transform in addition to the lecture prior to spring break. I ran into problems with partial fractions.
2. Any questions about the example above?
No, I found them to be straight forward.
3. Any comment on this assignment? (helpful, confusing, useful, irritating, etc – what did you think of it?)
When I run into problems with any course, especially when it comes to math I tend to look up lectures on YouTube my self, so I found these videos helpful and this preps for the lecture class.
Extra Credit:
Inverse Laplace Transform
F(s)=(s+5)/(s^(2)+6s+10)
1. I relearned how to do partial fractions, and reviewed the process on how to find LaPlace Transforms
2. No questions on the above example
3. The review of partial fractions was very helpful as it will allow us to find LaPlace Transforms with relative ease. The video that explained LaPlace transforms was very helpful as the instructor did a good job on elaborating the process to do the problems.
1. the video was pretty clear to understand the process of Laplace Transform of a Function
2. currently, no question.
3. it’s useful to learn and refresh memory
1. the video was pretty clear to understand the process of Laplace Transform of a Function
2. currently, no question.
3. it’s useful to learn and refresh memory
What is one thing you learned from (any) one of the videos? What is one thing that you didn’t understand, or found confusing?
I learned how to do LaPlace Transform. The videos were very helpful. I did not find anything confusing.
Any comment on this assignment? (helpful, confusing, useful, irritating, etc – what did you think of it?)
This assignment was very interesting and helpful. The example shown in the video was great.
Extra Credit:
Find the Laplace Transform of;
(((y)^2)-4)/((((y)^2)+4))^2)
the Laplace transform of (((y)^2)-4)/((((y)^2)+4))^2) is t*cos(2t) I believe.
1) I learned that Lapalace transforms seem pretty easy if you have a table, and don’t need to use partial fractions. And I also relearned my disdain for partial fractions.
2)Yes, will you please not give us a problem involving partial fractions on the test?
3)I like the idea of “flipping the classroom”, and I’m glad to finally have a professor try it out. I think it’s a great idea and I think we really need some alternative learning methods being used in schools.
1)What is one thing you learned in one of the videos?Whatis one thing you didn’t understand or found confusing ?
1)I learned how to do the Laplace Transform and the steps to do Laplace Transform just how it was explained in the class.I got little confused when 3 was multiplied tin numerator to match the equation from table.
2)Any questions about the examples obove?
2)No questions about the examples
3)Any comments about the assignment ?
3)it was good & helped better understand Laplace Transform Problems.
For extra credit Rodriguez.
Laplace transform the following
f(t) = (e^(3t))cos(9t))+t^(3)
find F(s)
I have learned how to do inverse Laplace transform, I have seen it in another class but it was confusing. These videos gave me idea about how to manipulate problems and use the table. I don’t have any question about the examples above. And these videos are helpful, some of them remind us about the partial fractions, which are always hard to figure out.
Extra Credit: (s^2)/((s^2)+49))+ (49)/(s-16)
I have learned how to do inverse Laplace transform, I have seen it in another class but it was confusing. These videos gave me idea about how to manipulate problems and use the table. I don’t have any question about the examples above. And these videos are helpful, some of them remind us about the partial fractions, which are always hard to figure out.
Extra Credit: (s^2)/((s^2)+49))+ (49)/(s-16)
1. I learned how to use the laplace transform.
2. no the example was pretty much straight forward.
3. The guy from the video gave a great example which help me understand the problem better.
1)What is one thing you learned in one of the videos?What is one thing you didn’t understand or found confusing ?
I learned how to do the Laplace Transform.I got confused when 3 was multiplied in numerator.
2)Any questions about the examples above?
No
3)Any comments about the assignment ?
The assignment was very cool and helpful.
What is one thing you learned from (any) one of the videos?
From the second video I was reminded of the fact that the a^2 for example 9 will be three in the LaPlace Transform solution and in the numerator it had to be 3*(16/3) in order to cancel out the three’s and remain with 16.
What is one thing that you didn’t understand, or found confusing?
It was simple, understood.
Any comment on this assignment? (helpful, confusing, useful, irritating, etc – what did you think of it?)
The assignment is beneficial such that the examples in the vids were explained well and it went along perfectly with your lectures, it’s a reinforcement of certain things in algebra and the laplace transform technique. Good assignment.
1)What is one thing you learned from (any) one of the videos? What is one thing that you didn’t understand, or found confusing?
I learned we are able to solve a differential equation by using the Laplace transform
2. Any questions about the example above?
Got stuck taking partial fractions.
3. Any comment on this assignment? (helpful, confusing, useful, irritating, etc – what did you think of it?)
Very helpful but I think it’s not a good way to tech high level of math special the partial fraction part
1. What is one thing you learned from (any) one of the videos? What is one thing that you didn’t understand, or found confusing?
Laplace Transform definitely makes differential equations much simpler, specifically into algebraic terms. What may take time to learn is the Inverse Laplace Transform, some problems require number arrangement and will only be easier when done many times.
2. Any questions about the example above?
It was confusing at first, but after seeing how it’s being dissected, specifically in the denominator, it became much more understandable.
3. Any comment on this assignment? (helpful, confusing, useful, irritating, etc – what did you think of it?)
I think integrating this type of “extra learning” is great especially for a class like this. Some times I may miss something that was said in class and I forgot to write it down. Assignments like this reinforce what was learned. Using videos from PatrickJMT and even KhanAcademy alongside for extra help is a useful resource. I think we all need it even if we don’t.
Extra Credit: Finding the Laplace Transform
12 + (e^6t)* cos(8t)