UPDATE 2: LaTeX power users. Advanced users can check out my additional 
UPDATE: LaTeX tester. Want to test out your LaTeX code before you post it in a comment? There is a LaTeX tester here, where you can type in your formula, hit the button, and see how it looks: http://samples.geekality.net/latex/
NOTE: When you use the test, do NOT include the dollar signs or the word “latex” — just include the stuff in between.
Assignment (due at midnight on Monday, February 20) . Create a problem that could appear on the first exam, and post it in a comment as a reply to this assignment. It should satisfy the following:
- It can be from anything we have studied so far this semester, from the first day of class up through Section 6.1, Areas Between Curves.
- It must be a reasonable exam problem — not too easy, not crazy hard (I will be the final judge of what counts as a “reasonable exam problem”). Make sure that you can solve your problem. For ideas, look at the homework assignments, the review sheet, the group work from class, your notes, and so on (you can use these sources as inspiration, but please don’t copy problems from them directly). If you wish, you can also ask short-answer, explanatory type questions, like “Explain in your own words ….” or “Why does …” or “What’s the difference between xxx and yyy?”. Bonus points for creative questions!
- It must contain some kind of mathematical symbols, which must be posted using correct mathematical notation. How do you do this? See below.
Extra credit. Solve one of your classmates’ questions, and post the solution as a reply. Your solution MUST be posted using correct mathematical notation.
What’s the point of this assignment? Two things: First, to make you think about what kinds of problems will be on the exam — and creating a problem forces you to consider this from a different perspective (what should be on the exam?) than simply practicing problems. Second, I want you to start learning how to type mathematics on the OpenLab — how do make integral signs, exponents, square roots, and so on?
Typing math on the OpenLab. This is not hard — BUT it takes a little getting used to. Here’s an example. If you type this into a comment:
Here is an integral: $latex \int x^2 dx$
then (after you post the comment) you should see this:
Here is an integral:
Each equation or expression begins with “$latex” and ends with “$”. The word ‘latex’, which appears after the first dollar sign, does not refer to the rubbery substance used in hospital gloves and sex toys, but rather to the incredibly powerful and awesome math typesetting language 
Here are a few more examples:
| Type this: | to get this result: | |
| A. | $latex \int_0^{\pi} \sin x dx$ |  |
| B. | $latex \frac{x+1}{x^2 + 5x}$ |  |
| C. | $latex \sqrt{x+1} + \sqrt[5]{x+6}$ | ![\sqrt{x+1} + \sqrt[5]{x+6}](https://s0.wp.com/latex.php?latex=%5Csqrt%7Bx%2B1%7D+%2B+%5Csqrt%5B5%5D%7Bx%2B6%7D&bg=ffffff&fg=000000&s=0 "\sqrt{x+1} + \sqrt[5]{x+6}") |
Some notes about these examples:
Example A (definite integral): Use curly braces “{ }” for grouping things together. On the integral sign, “_” gives a subscript and “^” gives a superscript, which is how we get the 0 and 
Example B (fractions): The code for fractions is “\frac{ }{ }”, with numerator inside the first set of curly braces { } and the denominator in the second set.
Example C (roots and radicals): Square roots and other roots like these
Hints and suggestions. Don’t start with a complicated formula. Write a comment with a short bit of math in it, and post it to see what it looks like. You can always edit the comment to make changes.
Stuck? Frustrated? Doesn’t look the way you want it to look? Let me know! Send me an email or simply post a question on the OpenLab — let me know what you’ve tried so far, and what you’re trying to accomplish.
For more examples, this link is a pretty good place to start. Want even more symbols? Here you go.
UPDATE:
You guys have been doing a great job typing math into your comments. You can feel free to ignore this, but if you’re interested in a few additional
1. Making the vertical bar stretch. For the vertical bar, which we use when solving a definite integral (in the step after we take the antiderivative but before we plug in) to keep track of the limits of integration: just use the vertical bar symbol “|” on your keyboard, usually located above the “\” symbol. BUT if you have a fraction or other piece of math that is taller than a single line, the “|” sign looks awfully small by comparison. How do we make it stretch vertically to match the stuff that comes before? We need to indicate to
$latex \left. \frac{x^2}{2} \right|_0^\pi $
which renders like so:
2. That pesky $. If you’re trying to discuss
u=5x+4
du=5 dx
1/5 $latex\int\(u)^3\du$
The integral of u^3 is u^4/4
1/5 x u^4/4= u^4/20 + C
Substitute u.
1/20 (5x+4)^4 + C
Hi debitcard,
In your response above, you simply need to add a space after the word “latex” — then it will show up correctly. Try editing your comment and see if it works.
-Mr. Reitz
Reitz,
I cannot seem to edit my original post.
u=5x+4
du=5 dx
1/5
The integral of u^3 is u^4/4
1/5 x u^4/4= u^4/20 + C
Substitute u.
1/20 (5x+4)^4 + C
debitcard, I think you’re looking for this
Substitute u.
Make sure to put a space between “$latex” and your formulae. Make sure to put the ending “$” directly after your last term– no space in between the two. Take a look at Mr. Reitz’s link to extra symbols and latex structures as well.
mansoorbaig: nice problem, and nice looking notation — thanks for being my first-post-er!
Hi Lance — you’re off to a good start. Two tips — you don’t need the backslash “\” in front of the number 4, or in front of the curly braces {} — get rid of these and I think your formula should display correctly.
Professor- I was testing it out. I wasn’t sure how exactly how to delete this post and it just remained there. I’ll make sure to give you a more concrete example. Thank you.
$latex\int_a^{\pi}frac\sqrt{2x+1}{x^10+\sqrt18x}dx$
Hi Mirza,
It’s a good start — here’s what to fix:
– insert a space after the word latex
– the keyword “frac” should have a space and a slash in front of it, like this:” \frac”
Try editing your answer and see if that works.
-Mr. Reitz
I tried but doesn’t works. I think the problem I wanted to write that’s too complicated. That’s why.
Hi Mirza,
Your problem is fine, and very close to complete. Here’s what your code looked like (for reference):
$latex \int_a^{\pi}\frac\sqrt{2x+1}{x^10+\sqrt{18x}}dx$
I think you are only missing the following — the top of your fraction should be enclosed in curly brackets { }, so the \sqrt{2x+1} should have { } around it. Also, your integral currently goes from “a” to “\pi” — you probably want to replace “a” with a number. Other than that, I think you’re good! Try submitting it again.
Regards,
Mr. Reitz
Your city is about to be the victim of a flood. In order to prepare for it, you decide to build a dam to stem the flood and then reservoirs to hold the excess water.
To Clarify: There is only one place where the flood can come from– it is one river.
Because you are so awesome, you happen to know that:
(or any even function with one absolute maximum and no absolute minimum). t stands for time in minutes; the flow rate is a function of time. Assume that all water flow as a result of this function will count of floodwater and will be carried into a reservoir
Water from the flood will flow inwards at a rate of
How long will the flood last?
Each reservoir can hold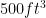
of water. How many reservoirs are necessary?
$latex \frac{\int_0^{100} -t^2 +100t}{500 ft^3}
That last part is:
Cool problem! I like the application – creative use of integration.
Just testing it out !! also if you guys want a template to preview your LaTeX use http://wordpress.com/#!/my-blogs/ i’m pretty sure it’s the same platform as open lab so you can hit preview when u try to make a new post 🙂
Thanks, Charles — that’s a nice tip (and yes, the OpenLab is based on wordpress so testing it there is a good strategy). If you don’t want to create a new wordpress site just for testing purposes, you can also check out the LaTeX code tester I posted at the top of the assignment (its http://samples.geekality.net/latex/).
Your mathematical notation is looking good 🙂
latex \int_4^{6} \frac{3x^2+\sqrt{x}}{x^2} dx
Nice!
$3x|_4^{6}-2x^-1/2|_4^{6}$
3(6-4)-2(6^-1/2-4^-1/2)
6+0.183
6.183
3x|_4^{6}-2x^-1/2|_4^{6}
3(6-4)-2(6^-1/2-4^-1/2)
6+0.183
6.183
3x|_4^6-2x^-1/2|_4^6
3(6-4)-2(6^-1/2-4^-1/2)
6+0.183
6.183
\int \frac{x}{\sqrt[5]{x+3}}dx
Answer:
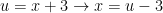
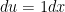
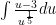
Great – but remember, for the extra credit, you have to post an answer to someone else’s problem.
Tricky one — I like it!
\int \frac{2}{5x^3}dx =
\frac{2}{5} \int \frac{1}{x^3}dx =
– \frac{1}{2x^2}
= – \frac{1}{5x^2}
\vert_2^{8} \cdots [ (-) \frac{1}{5(8)^2} – (-) \frac{1}{5(2)^2} ]
= \frac{3}{64} \equiv 0.046875
$latex \int \frac{2}{5x^3}dx =
\frac{2}{5} \int \frac{1}{x^3}dx =
– \frac{1}{2x^2}
= – \frac{1}{5x^2}
\vert_2^{8} \cdots [ (-) \frac{1}{5(8)^2} – (-) \frac{1}{5(2)^2} ]
= \frac{3}{64} \equiv 0.046875$
Hi Zekeba — Congrats on working out the LaTeX. You included a lot of it and managed to debug it, nice job! Some minor quibbles with the math but the essence is there, great work.
Jishan Biswas Math 1575 section 6638
Jishan Biswas , mat 1575 sec 6638
$latex\int cosx^2 sinx dx$
make a space after $latex
Do u mean that?
latex \int cos^2x sinx dx
or u mean that?
yes, that’s exactly what it is.
.
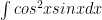Let u=cos x, then du= -Sin x dx
then $lateu- \int{u^2} du$
$-1/3u^3$
$-1/3cos^3x$
Let u=cos x, then du= -Sin x dx
then
$lateu- \int{u^2} du$
-1/3u^3
-1/3cos^3x
$u=cos x$
$du=-sin x$
$latex- \int{u^2} du$
$-1/3 u^3$
$-1/3 cos^3 x$
$u=cosx$
$du=-sinx$
$latex- \int{u^2} du$
$-1/3 u^3$
$-1/3 cos^3x$
Thanks for the clarification — I was wondering also. Looks good!
or This one?
u=cosx
du=-sinx
$latex- \int{u^2} du$
-1/3 u^3
-1/3 cos^3x
Zekeba Browne – MAT 1575 Section 6638 M/W 4:00 pm – 5:40 pm
The last part is to the power of 10 and then dx just to clear any confusion.
I see the dilemma — the “^” doesn’t realize that the 1 and 0 in the number “10” should be grouped together. To force them to both be up in the exponent, enclose them in curly brackets like so: ^{10}.
Using substitution rule.
u = x^{3} + 1
du=3x^2 dx
950941200.3 – 62.1
950941138.2 (ANS)
Formula Does not parse
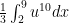
sorry it should be (du)
I see, thanks for the tip Prof. Reitz
du = 2x dx
0.45 + 0.5
0.95 (ANS)
Looks good!
X=3 u=ln3
X=1 u=ln1
0.442(ANS)
X=3, u=ln3
X=1, u=ln1
0.442(ANS)
Great.
Fengming Tan
sec#: 6637
Hi Fengming — is it possible you meant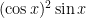
? As it stands, I’m not sure I know how to solve it!
Mr. Reitz
Sorry! The question is:
Just fine.
Joshua Ruiz – Section 6638
Hi Joshua — nice integral! BUT there is a problem — the function is not defined on the entire interval from -1 to 6 (or 6 to -1). For example, the secant function is undefined whenever cosine equals 0 (since secant = 1/cosine). To save the problem, either 1) remove the bounds and make it an indefinite integral, or 2) change the bounds to a smaller interval on which both secant and tangent are defined.
Mr. Reitz
Hmm, I should’ve paid more attention. I couldn’t get a working result testing out the integrals so I’m just going to change the bounds. Thank you for notifying me.
$latex \int 3x^2 \sec(x^3+1) \tan(x^3+7) dx \\
u=x^3+7 \\
du=3x^2dx \\
now\ you\ must\ resubtitute\\
\int \sec(u) \tan(u) du \\
z=\sec(u) \\
dz= \tan(u) \sec(u) du \\
\int z dz =\sec(u) = \sec(x^3+7)+C$
Hi Lance — this is a nice-looking integral, but I’m not sure how to find the antiderivative (I can’t figure out how to simplify it, and substitution doesn’t seem to work). Am I missing something? Try working it out — if it’s not possible, see if you can make a change of some kind.
Mr. Reitz
Melissa Miltz, section #6638 (M&W)
$\int\frac{2x^{2}+5\sqrt{x}}{x^{-4}}dx+\int\frac{6x^{2}}{5}dx$
\int\frac{2x^{2}+5\sqrt{x}}{x^{-4}}dx+\int\frac{6x^{2}}{5}dx
I like this one — looks nastier than it is, I think!
Mr. Reitz
that’s correct 🙂
A. Without any evaluation, explain in your own words which of these problems could yield an area.
B. In your own words, explain the difference between an area and a definite integral.
Khoreece Mendoza
MAT1575 M/W 4PM
Good questions — if you can get these ideas straight, and give a good explanation, you’re well on your way to developing a good intuition for integration.
Find the area that is formed by the curve of y = sin x and the x-axis from {0 , π}?
Find the area that is formed by the curve of y = cos x and the x-axis from {-π/2 , π/2} ?
I think these are reasonable problems and believe that if you can solve these, you understand the concepts and i think you’ll be able to do good on the exam?
Hi Gurpreet — I like these problems a lot! (but I notice you managed to avoid using
— post something else or repost with LaTeX for full credit).
Regarding your final question/comment, I’m not sure whether you are referring to a) your two problems above, or b) all the problems appearing in the comments so far. Certainly if you can do all the problems appearing so far, you’ll be well on your way to an A on the exam (but the examples we have are not exhaustive — there will be other things on the exam as well!).
Mr. Reitz
I read this late but i’ll re-post a new problem. And i was talking about all the comments/questions in the post were useful and you’ll do alright if you can solve them.
Here’s a simple problem.
1) f(x) = \int_0^2 \sqrt{2x + 1} dx
bettygeorge MA1575,6638
$latex\int_1^3(1/t^2-1/^4)dt$
\int_1^3(1/t^2-1/t^4)dt
Great!
sorry i left my question on your post by accident
Same problem as my response to Daniel Edwards — the notation looks good, but I don’t know how to solve it! Try to come up with a solution, and if not see if you can modify the problem to make it work.
Mr. Reitz
The notation looks great — but I’m not sure how to solve it! I could be missing something — do you have a solution? If not, try solving it and think about what you need to add in order to make it work — post an update with the results.
Mr. Reitz
\int_1^1(1+2y)^2 dy
\int_1^2(1+2y)^2 dy
disregard \int_1^1(1+2y)^2 dy… i made a mistake writting it….
Endri Domi
$latex\int_1^2(1+2y)^2 dy$
Hi vasquez — good problem! I think you just need to put a space after the work latex, and it should display correctly. Give it a try.
Mr. Reitz
Jeremy Li
Mat 1575 6637
Hi Jeremy — I posted this above but I’ll put it here in case you don’t see it there: The notation looks good, but I don’t know how to solve the problem! Try to come up with a solution, and if not see if you can modify the problem to make it work.
Mr. Reitz
Bibin Koshy
Mat 1575 6637
$latex\int_2^{4}\frac{dx}{x^2 + 5x}dx$
$latex\frac{1}{3}\int u^\frac{1}{2} du$
Final Answer: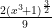
Keyla Arana, T & Th, 4:05-5:45
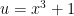
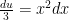
Error:
Final Answer: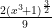
Also, forgot to add +C
u= x^3+1
du=3x^2 dx
(1/3)du= x^2 dx
= 1/3 ∫ (u)^1/2 * du
=∫ (1/3) * (2/3) u^3/2 + c
= ∫ 2/9 * ( x^3+1)^3/2 + c
koshygkoshy — the notation looks fine (if you insert a “dx”), but the integral is hard! I’m not sure how to find the antiderivative — see if you can work it out, and either post a solution or modify the problem. Thanks,
Mr. Reitz
Evaluate the indefinite intergal:
$latex\int \frac{cos\sqrt{x}}{\sqrt{x}} dx$
$latex\int \frac{cos\sqrt{x}}{\sqrt{x}} dx $
http://s.wordpress.com/latex.php?bg=%23ffffff&fg=%23000000&s=2&latex=latex%5Cint%5Cfrac%7Bcos%5Csqrt%7Bx%7D%7D%7B%5Csqrt%7Bx%7D%7D+dx+
latex \int \ frac{ cos\ sqrt{x}}{\ sqrt{x}} dx
Evaluate the indefinite intergal:
$latex\int \frac{cos\sqrt{x}}{\sqrt{x}} dx $
Evaluate the indefinite intergal:
nice problem, and great debugging work. You did it!
Mr. Reitz
$latex/int_2^{/3}/frac{dx}{(x-2)}$
What did i do wrong? i cant get the image..
mon/wed 4-540
latex$ \int_2^{4x^5}\frac{\sqrt{\sin x+1}}{x^2}dx$
Keyla Arana
Why is this always messing up..? Ignore the top one..
Keyla — the notation looks good! But I’m confused by the upper bound of
in the integral. Is it supposed to be there?
)
Mr. Reitz
(ps. just had a thought — is it a “find the derivative” problem? if so, change each “x” to a “t”, except the
Yes, sorry, i forgot to change the variable, it’s supposed to be t’s.
Great — nice problem! (To clarify, the problem instructions should read “find the derivative”).
Hi Lance — this is a nice setup, but hard problem! I can’t see how to make substitution work — try it, and modify the question if necessary.
Mr. Reitz
Jiarong Mei section 6638
Great 🙂
Theo Zeng section 6638
i was told this wasn’t the final asnwer there is more but i’m at a loss
actually
you cant put a solved integral inside of the unsolved
Great problem but quite tricky, unless you really remember your trig identities!
sub
u= $latex\{e^x+1}$
du= $latex\{e^x dx}$
= $latex\int\sqrt{u}du$
$latex\int\sqrt{u}$ = $latex\frac{2u^3/2}{3}+C$
substitute
$latex\{e^x+1}$
for u
=$latex\frac{2/3(e^x+1)^3/2}/+C$
My mistake.. I meant to reply to tonymei999’s post.
I see my work looks perplexed.
Jishan mat1575, section 6638
Simple looking but deadly! How do we find the antiderivative of ln x? This is worth playing around with, but I would NOT ask it on this exam.
Mr. Reitz
Posted by Stanislav Podolski MAT 1575 – 6638.
Hint: This integral is nor very complicated, but it makes you remember some trigonometry.
how would you go about this ? using the sin^2 identity then doubling it?
You can start by doing the following:
=
= …
Formula did not parse(
well basically to start you have to represent sin^4x as (sin^2x)^2.
I agree — definitely a challenge, unless you remember your trig identities!
sweet!
Amanpreet
1/4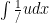
1/4log (x(x^3+4)) + c
1/4 (log(x^3+4)+log(x))
1/4 $latex \int \frac (1)(u) dx
1/4log (x(x^3+4)) + c
1/4 (log(x^3+4)+log(x))
1/4 $latex \int \frac (1/u) dx
1/4log (x(x^3+4)) + c
1/4 (log(x^3+4)+log(x))
$latex \int lnx+4x^2-2x+4
Look good
yes, but very simple.
^ Find the integral ^
Koonhoi Xie MAT 1575 – 6638.
Find the integral between two curves given the function x & x^2
Hint*- Start by finding the point of intersection.
Formula is given by $latex\int_a^bf(x)-g(x)dx$
Koonhoi — looks good! Your formula just needs a space after the word latex.
Thanks, Reitz.
Last part is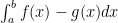
\int\frac{\sin {x}}{1+\sin{x}}dx
Hi Kedeshia — you just need to put “$latex” at the start and “$” at the end, and your code should display correctly. However, I think your problem is hard — I can’t figure it out! Try it, and see if you can make it work, or make a modification.
nazir ahmed math1575-6638
Looks nice, but I can’t figure it out! Am I missing something?
Mr. Reitz
Looks good!
Cool problem – but I don’t see the solution! Try to make it work, and let me know what you find.
Mr. Reitz
$latex\frac{x}{\sqrt[6]{x+3}$
$latex\frac{x}{\sqrt[6] x+3}$
You’re close! Just add a backslash “\” before the word “frac”.
Mr. Reitz
(ps. I’m not sure how to solve this problem!)
Antonio Downer
Math 1575-6638
Hi Antonio — I think the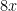
should be on the top, not the bottom (unless I’m missing something). Try it out, and let me know.
Mr. Reitz
Your correct, my mistake.
Oops..
Great !
Good!
u=
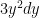
du=
dy= du/3y^2
int\ y^2cos(u)* (1/3y^2)du
int\ cos(u)/3 du
the integral of cos(u) is sin(u) => sin(u)/3
replace: u=y^3
answer: $latex \frac{sin y^3}{3}
$late\int(1-t)(2+t^2)dt$
Just add the letter x to latex, and a space after the x — then it should work.
Looks nice! BUT I don’t know how to solve it… Try to find a solution, and if it doesn’t work out try modifying the problem.
$latex\int\ 2x(x^2+4)^{100}$
plug in:
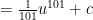
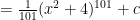
Looks good!
^ -Mahendra Seepersaud MAT1575-6637
Hi Mahendra — good problem! Just change the parentheses ( ) to curly brackets { }. That will put the entire expression
into the exponent.
Good .
Just fine .
Hi Tiff — you’re close! Get rid of the backslash in front of the x, and it should display properly. Quick question: is this a “find the derivative” problem? If so, convert the x’s (except the first one) to t’s, and add the instructions “find the derivative”.
Looks fine.
Drake Li Section 6638
The answer will be the following :
1 + sin (5) – cos (5)
1 + ~-.96 – ~.28
ANS : .24
this one is real..
Hi aman – just put the 6x into curly brackets { } to make them both appear in the exponent. However, if we do this, I don’t know how to solve the problem! See if you can solve it, or make a change.
^ Lukasz Boruch
Looks good.
Find the area between y=x^2 and y=x^3 between x=0 and x=1 when the function is given:
&latex \int (x^2 – x^3) dx$
Weird – your formula should work, but doesn’t. After investigating, it seems that the minus sign in the middle is not a standard “dash”, but is a slightly longer dash character. Try deleting it, and typing it in again.
A company produces \int_\frac{x^2}{\sqrt{X}} solar panels an hour. How many panels will be made in six hours?
You’re off to a good start, but the question needs a bit of modification — I’m not sure how to solve it from the information given! For notation, don’t forget to include the “$latex” at the start, and “$” at the end.
Drake Li Section 6638
Drake – the notation looks good! BUT the problem has problems — I’m not sure how to find the antiderivative of cscx or secx. In addition, there are places between 0 and pi where these functions are not defined (for example, secx = 1/cosx, which is undefined when sinx equals 0).
Oops, how about this question?
Sure – looks good 🙂
Alexander Barbaran 7216
it doesn’t work if i use \int 0^{3\pi} \frac \sqr{x+3} \sqr[3]{x-6}
Hi darklor7 – you’re on the right track! You need to put an underscore “_” before the zero to make it show up as the lower bound of integration. The code for the radical sign is \sqrt, not \sqr (don’t forget the t). Finally, after \frac, the numerator and denominator should each be enclosed in curly brackets { }, so it would start like this: “\frac{\sqrt{x+3} …” and so on. Give this a try and see if you can make it work.
-Mr. Reitz
∫ X^2+4x dx
Hi Prosenjit — the problem is fine, but you need to put it into latex so that the notation displays correctly! See if you fix it and re-post.
Thanks,
Mr. Reitz
a problem that I always didn’t know how to solve but one we took the test i lean how to solve it
$latex\int_0^{5}{\frac{\sqrt[3]{27}}{\sqrt[3]{{(x-3)}^4}}}dx$
latex\int_0^{5}{\frac{\sqrt[3]{27}}{\sqrt[3]{{(x-3)}^4}}}dx
$latex\int_0^{5}{\frac{\sqrt[3]{27}}{\sqrt[3]{{(x-3)}^4}}}dx$
$ latex\int_0^{5}{\frac{\sqrt[3]{27}}{\sqrt[3]{{(x-3)}^4}}}dx$
$ latex \int_0^{5}{\frac{\sqrt[3]{27}}{\sqrt[3]{{(x-3)}^4}}}dx $