Section 11.4-Exercise #14
Header Image
Creative Commons image courtesy of Flickr user StormPetrel1-
Recent Posts
Recent Comments
- In the Spotlight: MAT2540 – Discrete Structures and Algorithms II – The Open Road on Links
- OpenLab Workshop for Opening Gateways Fellows | 2018-2019 Opening Gateways Faculty Seminar on Final Exam Review
- Eric on Eric’s Final Review
- Kate Poirier on Hints/reminders from today’s class
- Kate Poirier on Final Exam Review
Archives
Categories
Meta




Can you type the question please?
You did this question wrong.
[url=http://postimg.org/image/4giluw8xt/][img]http://s16.postimg.org/4giluw8xt/20160330_094841.jpg[/img][/url]
Sorry about that link, I thought it would work.
Here is the correction : http://rpubs.com/thebunnyknight/167294
Hi Bryan and Eric,
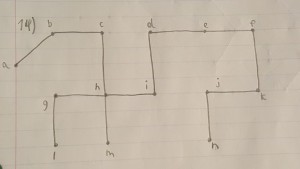
After looking a bit more carefully, I see a little issue with each of your answers. Eric found the issue with Bryan’s: it looks like Bryan has performed a good depth-search algorithm, but he’s ignored the instructions about the alphabetical ordering of vertices. So it looks like Bryan added the edge (h,m) before adding (h,i), but since i comes before m in the alphabet, he should have pursued the path beginning with (h,i) first (as it looks in his figure). If he were to do that, he’d eventually backtrack until the first chance he’d have to include the vertex m, so that’d be by adding the edge (i,m).
Eric, I hadn’t noticed when I first looked at your answer, but it looks like there’s an issue with your application of the depth-first algorithm. Beginning with the vertex i, the first edge you’d add is (i,d), then (d,e), then (e,f)…it looks like you’ve gone this far and then stopped at f. However, k is not already included in the spanning tree, so you should go ahead and include (f,k), then (k, j), then (j,n) before backtracking.
Here’s the order I added edges: (a,b), (b,c), (c,h), (h,g), (g,l), (h,i), (i,d), (d,e), (e,f), (f,k), (k,j), (j,n), (i,m).
Hope that clarifies things!
We can’t add (i,d) to the depth-first algorithm until we back track because they aren’t alphabetical and adding (i,j) at that point is warranted because it allows us to make longer, the initial alphabetical path.
The order that takes into account the alphabetical nature of the problem would move to (i,j) instead of (i,d).
Shouldn’t the order of added edges be any of these: {B(x,y) would be a vertex reached when invoking a backtrack with any subsequent edge resulting from that backtrack}
Choice 1
(a,b), (b,c), (c,h), (h,g), (g,l),
B(h,i), (i,j), (j,k),
B(j,n),
B(i,d), (d,e), (e,f),
B(i,m).
Choice 2
(a,b), (b,c), (c,h), (h,g), (g,l),
B(h,i), (i,j), (j,n),
B(j,k),
B(i,d), (d,e), (e,f),
B(i,m).
Choice 3
(a,b), (b,c), (c,h), (h,i), (i,j), (j,n),
B(j,k),
B(i,d), (d,e), (e,f),
B(i,m).
B (h,g), (g,l),
Choice 4
(a,b), (b,c), (c,h), (h,i), (i,j), (j,k),
B (j,n),
B(i,d), (d,e), (e,f),
B(i,m).
B (h,g), (g,l),
In all of these choices the first run of the depth-first algorithm is the longest it can be while satisfying the alphabetical clause. The only time we don’t follow the alphabetical clause is when we backtrack to get the vertices that weren’t alphabetically adjacent to a given vertex or if we had a choice between two satisfactory vertices.
actually, technically speaking, you can backtrack from k,j or i to get to d,e,f but i-vertex is the only one that would put d,e,f in alphabetical order which is why I chose i-vertex.