Hi Kamil. This mostly looks very good. I do have two comments, though.
First, when you’re showing that is , you have 3 inequalities that hold when ; the right-hand-side of each is . When you add up the left sides of these inequalities, you get but when you add up the right side, you get which is . This tells you that for , you have . But you have written . Following this through, your value of should be , not .
Next, when you’re showing that is not , it looks like you’ve shown that the particular choice does not work. This is not enough to show that is not . Instead you want to show that there are NO POSSIBLE CHOICES of that work. Try setting up a proof by contradiction to see this formally. (BTW I added a comment to Christian’s post that included a proof by contradiction for another set of functions…that might be useful for you to look at.)
Hi Kamil. This mostly looks very good. I do have two comments, though.
First, when you’re showing that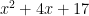 is
is 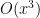 , you have 3 inequalities that hold when
, you have 3 inequalities that hold when  ; the right-hand-side of each is
; the right-hand-side of each is  . When you add up the left sides of these inequalities, you get
. When you add up the left sides of these inequalities, you get 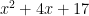 but when you add up the right side, you get
but when you add up the right side, you get  which is
which is  . This tells you that for
. This tells you that for  , you have
, you have  . But you have written
. But you have written  . Following this through, your value of
. Following this through, your value of 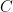 should be
should be 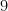 , not
, not 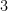 .
.
Next, when you’re showing that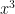 is not
is not  , it looks like you’ve shown that the particular choice
, it looks like you’ve shown that the particular choice  does not work. This is not enough to show that
does not work. This is not enough to show that 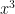 is not
is not  . Instead you want to show that there are NO POSSIBLE CHOICES of
. Instead you want to show that there are NO POSSIBLE CHOICES of  that work. Try setting up a proof by contradiction to see this formally. (BTW I added a comment to Christian’s post that included a proof by contradiction for another set of functions…that might be useful for you to look at.)
that work. Try setting up a proof by contradiction to see this formally. (BTW I added a comment to Christian’s post that included a proof by contradiction for another set of functions…that might be useful for you to look at.)