Section 3.2 Number 19
Header Image
Creative Commons image courtesy of Flickr user StormPetrel1-
Recent Posts
Recent Comments
- In the Spotlight: MAT2540 – Discrete Structures and Algorithms II – The Open Road on Links
- OpenLab Workshop for Opening Gateways Fellows | 2018-2019 Opening Gateways Faculty Seminar on Final Exam Review
- Eric on Eric’s Final Review
- Kate Poirier on Hints/reminders from today’s class
- Kate Poirier on Final Exam Review
Archives
Categories
Meta

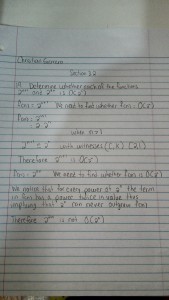



Hi Christian, this looks pretty good! I have a comment about the first part, where you’re showing that is
is  . You have a statement that reads, “
. You have a statement that reads, “ .” This statement as written is false. All is not lost, though, because I don’t think it was the statement you intended to write. Here’s a suggestion for a possible change: “Since
.” This statement as written is false. All is not lost, though, because I don’t think it was the statement you intended to write. Here’s a suggestion for a possible change: “Since  , we have that
, we have that  for all values of
for all values of  . Since
. Since 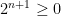 , this implies that
, this implies that 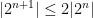 for all values of
for all values of  . Therefore,
. Therefore,  is
is  with witnesses
with witnesses 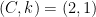 .” (Note that setting
.” (Note that setting  here is a choice…we could have chosen any positive value for k.)
here is a choice…we could have chosen any positive value for k.)
I also have a comment about your second part! What you’ve written describes an intuitive understanding of what’s going on, but it’s not a formal proof. Here’s one way to prove the statement formally.
We’ll prove that is not
is not  . This will be a proof by contradiction. This means that we’ll assume that
. This will be a proof by contradiction. This means that we’ll assume that  is
is  and try to derive a contradiction. Since
and try to derive a contradiction. Since  is
is  this means that there exists a pair of positive constants
this means that there exists a pair of positive constants  such that
such that  for all
for all 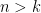 . Since both
. Since both 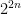 and
and 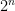 are
are  for all values of
for all values of  , we can remove the absolute value bars, so
, we can remove the absolute value bars, so 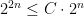 for all
for all 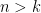 . The function
. The function  is an increasing function, so you can take
is an increasing function, so you can take  of both sides without changing the inequality. This tells us that
of both sides without changing the inequality. This tells us that 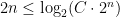 for all
for all  . The right-hand-side is equal to
. The right-hand-side is equal to 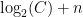 (using log rules). Therefore, we have that
(using log rules). Therefore, we have that 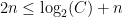 for all values of
for all values of 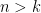 . Subtracting
. Subtracting  from both sides, this means that
from both sides, this means that 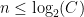 for all
for all 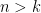 . But this is a contradiction! The value
. But this is a contradiction! The value  can’t stay below the value
can’t stay below the value 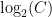 for ALL
for ALL 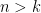 . Therefore, there can exist no pair of positive constants
. Therefore, there can exist no pair of positive constants 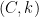 so that
so that  for all $\latex n>k$. This means that
for all $\latex n>k$. This means that  is not
is not  .
.