Group Members: Aram C., Louis C.R., Joseph G., Patrick P.-O., Erik S.C.
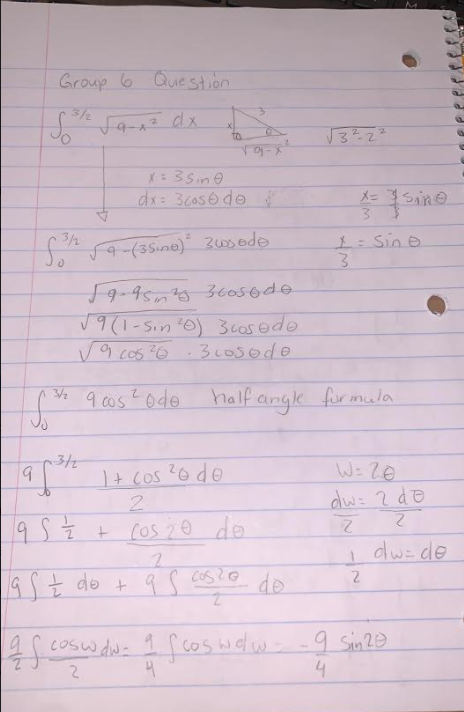

Professor Kate Poirier | OL30 | Fall 2020
Group Members: Aram C., Louis C.R., Joseph G., Patrick P.-O., Erik S.C.
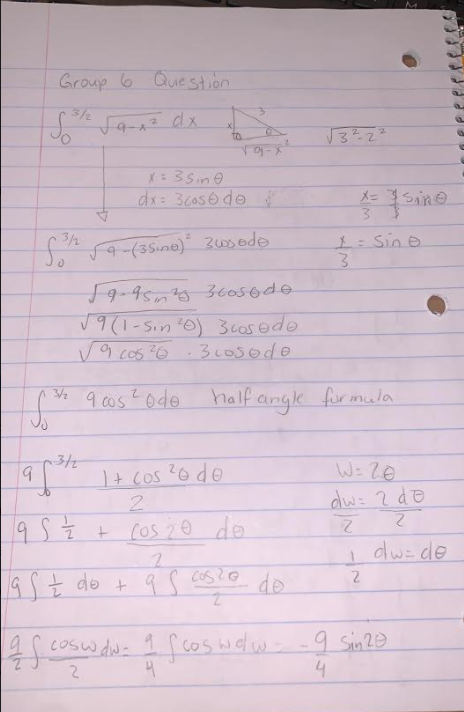

Group members: Shah A., Rafael D., Vishal R., David T., Anthony R.
Here are the solutions we have produced:

Here is Anthony’s solution for this problem (step-by-step):
1. Start by thinking what trig identity you should use. In this case, since it is the square root of (x2 + a2) where a is a constant, you will use 1 = tan2θ = sec2θ.
2. Model your triangle where you put the square root of (x2 + 9) as the hypotenuse, the number 3 as the adjacent leg, and the variable x as the opposite leg.
3. Let x = 3tanθ, and find its derivative. The dx = 3sec2θdθ. Then multiply values by dx/x.
4-5. Begin simplifying the values. In this case, 9 × 3 = 27, and then 27 ÷ 9 = 3.
6. Use the constant multiple rule by taking out the number 3 from the integral.
7. Factor out the square root of (9tan2θ + 1). It becomes secθ × 3.
8. Simplify: 3 × 1/3 = 1, and sec2θ divided by secθ equals to just secθ.
9. Take the trig functions in terms of cosine and sine. Then, simplify accordingly.
10. Perform u-substitution- since du/u fits the form perfectly. (Note in Step #10, it is (cosθ ÷ sin2θ) dθ.
11. Integrate the values by using the power rule.
12. After you integrate, add +C at the end, and simplify.
13. Since -1 is in the denominator, multiply (or divide) the entire equation by negative 1.
14. Put the values back. In the event of using a negative exponent, use cscθ instead of sin-1θ.
15. Put the trigonometric values in terms of x. Remember what you did to the model triangle. In case of cscθ, use the values of (hypotenuse / opposite).
Group Members: Kevin V., Davide B., Kai H.-L., Jia Hong Y., Yanzu Z.

© 2024 MAT1575 Calculus II
Theme by Anders Noren — Up ↑
Recent Comments