Group members: Dixon Bonilla, Imane Sama, and Ines Bissat.

Professor Kate Poirier | OL30 | Fall 2020
Group members: Dixon Bonilla, Imane Sama, and Ines Bissat.


Group 2: Stewart B. , Alejandro D. , Aaron L. , Pablo.S , Jordan W.
Prof Poirer
MAT 1575- OL30
September 27, 2020
Secretary: Aaron Libato
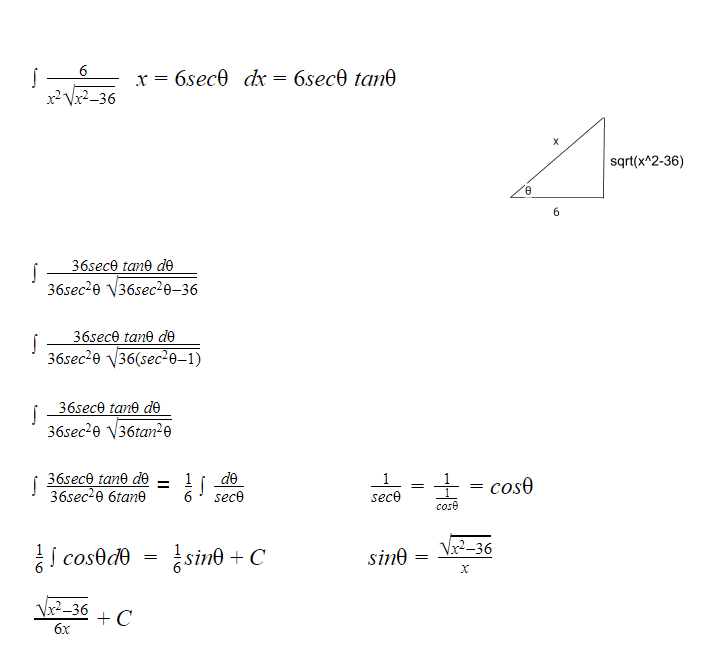
Problem:
Work:
1) Starting from the indefinite integral of 1/((x^2) sqrt(36-x^2) dx, use integral substitution by having x = sqrt(36-x^2) then converting into x = (sqrt(36) / sqrt(x^2)) * sin(u) which then becomes x = 6sin(u) from which you can obtain dx = 6cos(u)
2) Substitute the x into the original problem to result in:
Indefinite integral of (1 / (6sin(u)^2)( sqrt(36 – 6sin(u))^2)) * 6 cos(u) du
3) Simplify in order to receive (6 cos(u) / ((6^3)sin^2(u))(sqrt(-sin^2(u)+1)) du
4) Cancel the 6 from the numerator and denominator as well as use the trig identity of
cos^2(x) + sin^2(x) = 1 in order to get (cos(u) / ((6^2)sin^2(u))(sqrt(cos^2(u)))) du
5) Further simplify using exponent and trig identity of cos(x)/sin(x) = cot(x) in order to get
cot(u) / ((36)sin(u)) (sqrt(cos^2(u)))) du
6) Use the trig identity of cos(x)sin(x) = sin2x/2 in order to simplify into
(cot(u) / (36sin(u)) (sin2(u)/2) du
7) Simplify into (cot(u) / 18 sin2u) du
8) Remove the constant to get (1/18) indefinite integral cot(u)/sin2(u) du
9) Use the trig identity sin2x = 2cos(x)sin(x) to get
(1/18) indefinite integral (cot(u) / 2cos(u)sin(u)) du
10) Remove the constant again to get
(1/18)(½) indefinite integral (cot(u) /cos(u)sin(u)) du
11) Multiply the constants and use the trig identities of cot(x) = cos(x)/sin(x) as well as 1/sin(x) = csc(x) in order to get
(1/36) indefinite integral csc^2(u) du
12) Solve indefinite integral to get (1/36) -cot(u) then sub u with arcsin(⅙)x which is obtained from x = 6sin(u):
(1/36) -cot(arcsin(⅙)x
13) Use trig identity of cot(arcsin(x)) = sqrt(1-x^2) / x in order to get
(1/36) – sqrt(1- (⅙) x^2) / (⅙)x
14) After multiplying and simplifying, the final answer is
Indefinite integral of (1/(x^2)(sqrt(36-x^2))) dx = (-sqrt(36-x^2) / 36x) + C
Group 6 members: Aram C., Louis C.R., Joseph G., Patrick P.-O., and Erik S.C.
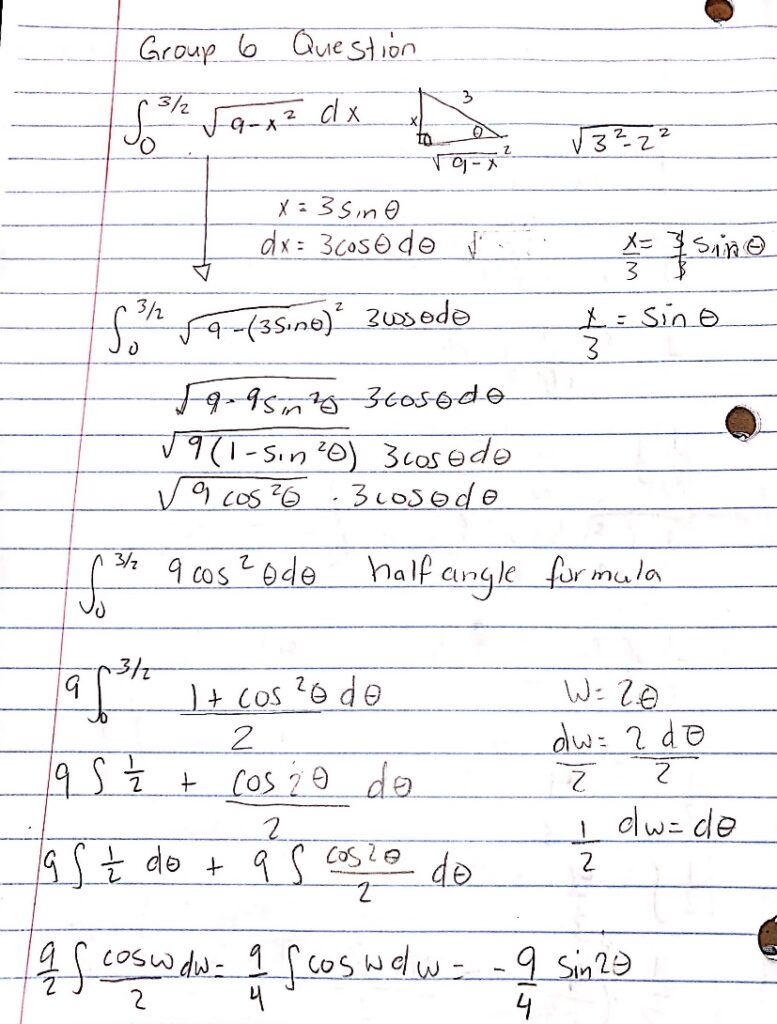
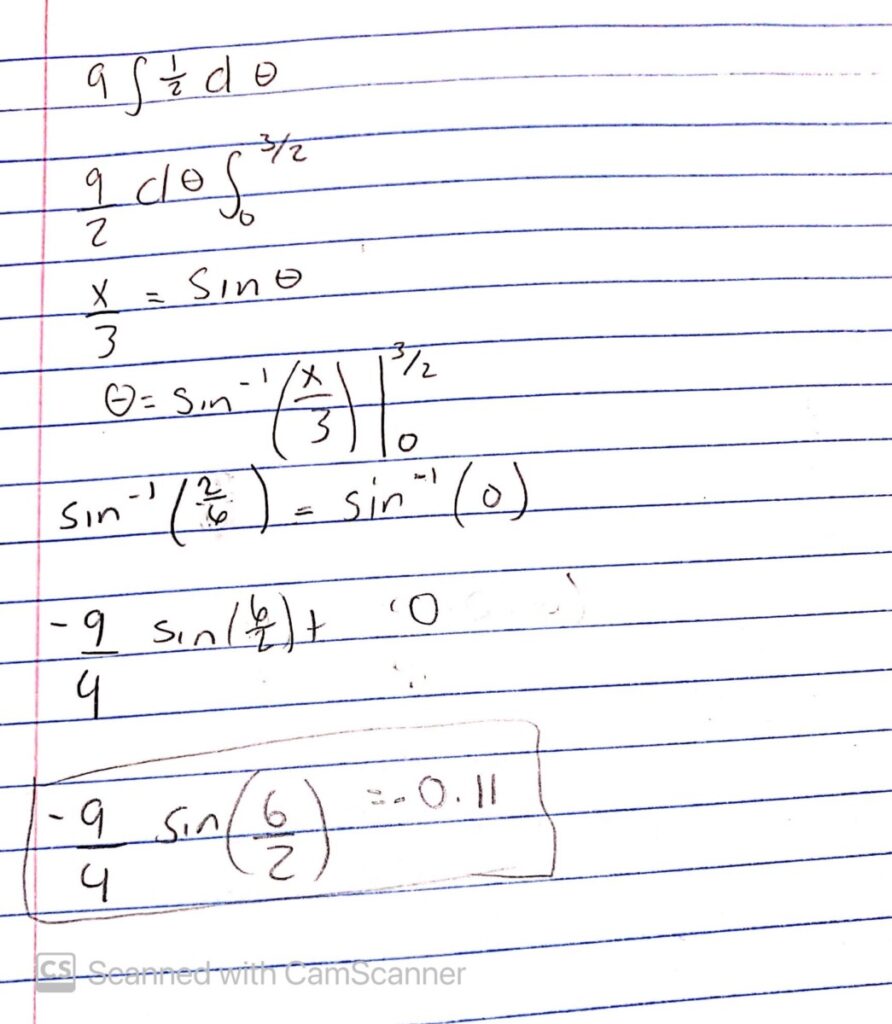
© 2025 MAT1575 Calculus II
Theme by Anders Noren — Up ↑
Recent Comments