Hi all, here is my new (and refined) solution for #6 (integration by parts). It is important to know when to choose u in this order: (Log, Inverse, Algebraic, Trig, Exponential). My solutions are reviewed by Shah Ahmed and Rafael Diez.

Professor Kate Poirier | OL30 | Fall 2020
Hi all, here is my new (and refined) solution for #6 (integration by parts). It is important to know when to choose u in this order: (Log, Inverse, Algebraic, Trig, Exponential). My solutions are reviewed by Shah Ahmed and Rafael Diez.

Group members: Anthony Regner (secretary), Shah A., Rafael D., Vishal R., David T.
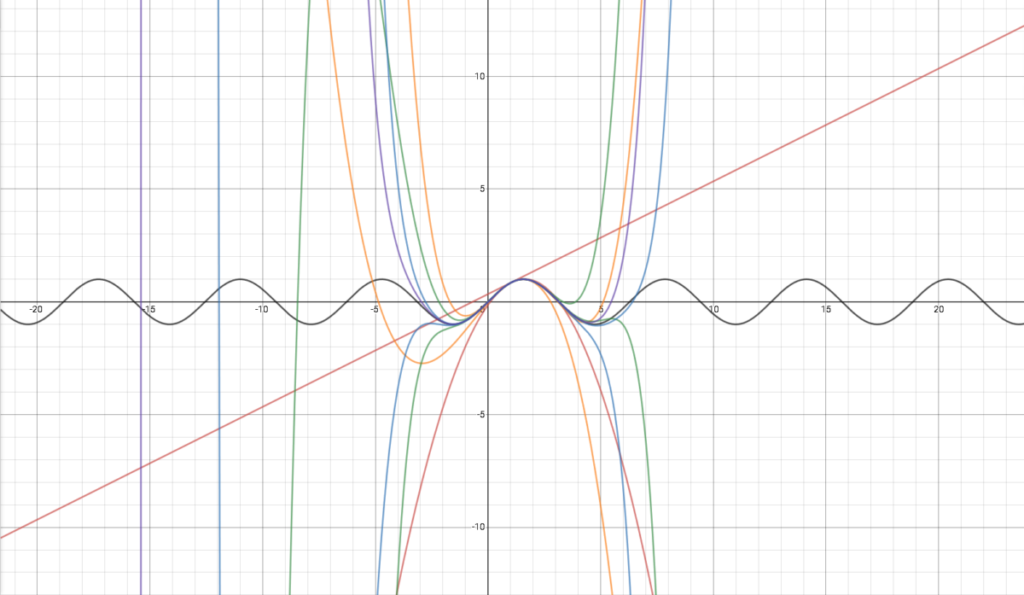
Hi everyone! This is Anthony here again. For this assignment, we found the ninth degree of the Taylor Polynomial such that f(x)=sin(x), and center a = pi/3.

Desmos link: https://www.desmos.com/calculator/ztvawbhq0f
Good evening all! Since test #1 is coming up on next Thursday (10/8/2020), it is important to review all of the integration techniques we have learned so far. Integration by substitution is one of them!
I have decided to do problems #9 and #14 in the Integration by Substitution homework set in WeBWorK. This post will be updated over time based on feedback I receive.

Note: Since 422 is an extremely large number, I have to round this number to three significant figures (1.76 × 1013), and use scientific notation in this case.
With enough simplification, you will notice that the denominators are alike, and you can now combine -5 and +5.
Therefore, the definite integral is 0.
© 2025 MAT1575 Calculus II
Theme by Anders Noren — Up ↑
Recent Comments