Author: Jacky
Version B, Question 9
Let f(x)=(x-1)/(x+2). Determine whether f(x) is invertible. If f(x) is invertible, find its inverse. If f(x) is not invertible, explain why not.
First replace f(x) with y.
y=(x-1)/(x+2)
Next switch x with y.
x=(y-1)/(y+2)
Multiply both sides by (y+2)
x(y+2)=(y-1)
Distribute
xy+2x=(y-1)
Rearrange the terms.
xy-y=-2x-1
Factor out y
y(x-1)=-2x-1
Divide both sides by (x-1)
y=(-2x-1)/(x-1)
Replace y with f^-1(x)
f^-1(x)=(-2x-1)/(x-1)
f(x) is invertible.
WeBWorK
Functions – Inverse Functions: Problem 9
If f(x)=(2x-8)/(5x+4), find the inverse function.
First we interchange x and y:
x=(2y-8)/(5y+4)
Next, we multiply both sides by 5y+4:
x(5y+4)=2y-8
Distribute the x:
5xy+4x=2y-8
Rearrange the terms:
4x+8=2y-5xy
Factor out y:
4x+8=(2-5x)y
Divide both sides by (2-5x):
(4x+8)/(2-5x)=y
Replace y with f^-1(x):
f^-1(x)=(4x+8)/(2-5x)
Hello! My name is Jacky and I am majoring in Electrical Engineering. I will be taking Calculus 1 after Mat 1375. After graduating I hope I can go travel for a few months. I like listening to music and playing games. Something I am good at is taking naps. My favorite animal is a turtle.






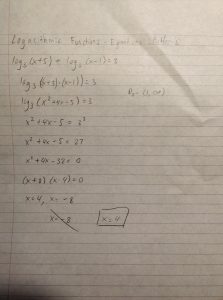
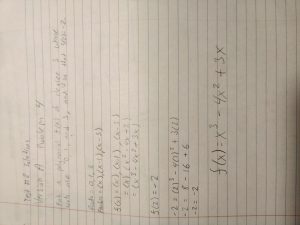





Recent Comments