Author: Suman Ganguli (Page 2 of 16)

A set of Practice Final Exam exercises is available in WebWork. Submit written solutions to your exercises on Blackboard by Monday night (Dec 14). Your written solutions will be graded and counted as a quiz.

Note: This WebWork set is set up as a test with a 2h time limit, but you can ignore the time limit and the corresponding “recorded score.” You can still use WebWork to check your answers, but you should focus on understanding the exercises and writing up complete solutions.

The final exam will be Wed Dec 16-Fri Dec 18, and will be very similar in format to this Practice Final Exam.

Here is a guide to the exercises, with notes on examples to review from the WebWork, from the various quizzes and exams, from examples I have posted on OpenLab, and from the textbook:

1. Inequalities:
   • absolute value inequality – show algebra leading to solution set (see WebWork “Absolute Value Inequalities”; Quiz #1; Exam #1)
   • polynomial inequality – show algebra solving for x-intercepts, then sketch graph to show solution set of inequality or use “test points” in each subinterval to find solution set (see WebWork “Polynomial Inequalities”; Exam #2; textbook Example 12.2)
   • rational function inequality- show algebra solving for x-intercepts and vertical asymptotes, then sketch graph or use “test points” in each subinterval to find solution set of inequality (see see WebWork “Rational Inequalities”; Exam #2; textbook Example 12.4)
2. Rational function (show all algebra for finding domain, asymptotes, roots/intercepts; sketch a graph of the function and label all of these features):
   • see WebWork “Rational Functions – Comprehensive”; Exam #2; textbook Example 11.5
   • see this Rational Functions Example
3. Difference quotient or inverse of a function:
   • see WebWork “Functions – Difference Quotient”; Exam #1
   • see WebWork “Functions – Inverse Functions”; textbook Example 7.6 (pp89-90)
4. Polynomial function (show all algebra necessary for factoring and finding roots, including long division; sketch a graph of the function and label the x-intercept(s) and y-intercept)
   • see WebWork “Polynomials – Graphs”; Quiz #3; Exam #2
   • see this example
5. skip this exercise
6. Logarithmic function or logarithmic properties:
   • see WebWork “Logarithmic Functions – Graphs”; textbook Example 13.3
   • see WebWork “Logarithmic Functions – Properties”; textbook Example 14.3
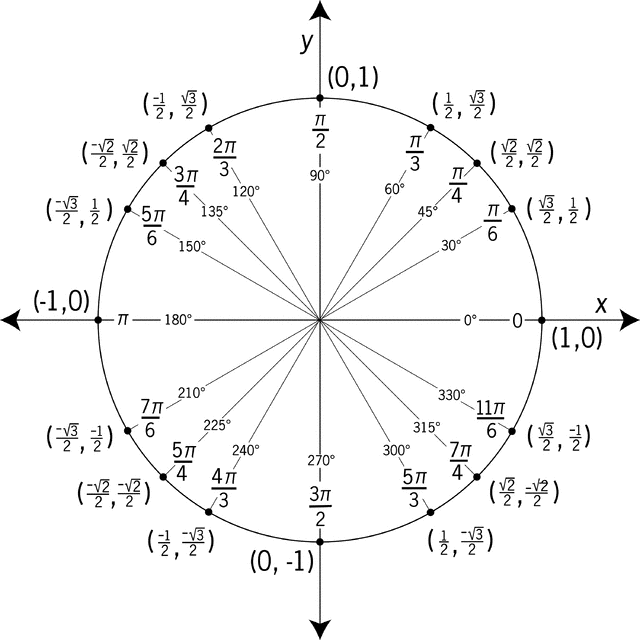
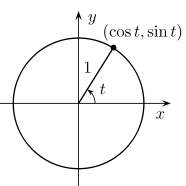
7. Trigonometric function and graph:
   • see textbook Definition 17.9 and Example 17.10 (pp246-247)
   • sketch a graph of the function and label the period, amplitude, and phase shift
8. Trigonometric equation (show algebra needed to simplify the equation, and then justify your solutions in terms of either the unit circle or the graph of the trig function involved)
   • see WebWork “Trigonometry – Equations”
9. Application of exponential function:
   • see WebWork “Exponential Functions – Growth and Decay”
   • see two examples from that WebWork set posted here
10. skip this exercise