Lesson 17: Alternating Series

Motivating question

Many of the tests in our series convergence/divergence toolbox assume that all the terms in a given series or positive. These tests can also be used when all the terms are negative. But most series have terms of different signs. One special way for a series to have terms of different signs is when they alternate. So what can these alternating signs tell us about the convergence or divergence of a series?

Motivating example

Beginning with Warmup exercise 1, we’re getting a sense that the alternating harmonic series

\[\sum_{n=1}^\infty (-1)^{n+1}\frac{1}{n} = 1- \frac{1}{2}+ \frac{1}{3}-\frac{1}{4}+\frac{1}{5}- \frac{1}{6}+\frac{1}{7} \dots\]

might converge. This might seem surprising because we know (using the integral test for example) that the harmonic series

\[1 +\frac{1}{2}+ \frac{1}{3}+\frac{1}{4}+\frac{1}{5}+ \frac{1}{6}+\frac{1}{7} \dots\]

diverges. So adding a sign so that the terms alternate between positive and negative makes a big difference. To strengthen our intuition for this example, let’s plot the terms in the sequence of partial sums. Figure 1 below shows a graph of the first several partial sums. Click on Figure 1 to open up an interactive Desmos graph (link here as well). Use the slider for $b$ in the upper left of the screen to drag the red horizontal line up and down until it looks like the green plotted points will converge to that line as the number of terms approaches infinity. At what height is your red horizontal line?

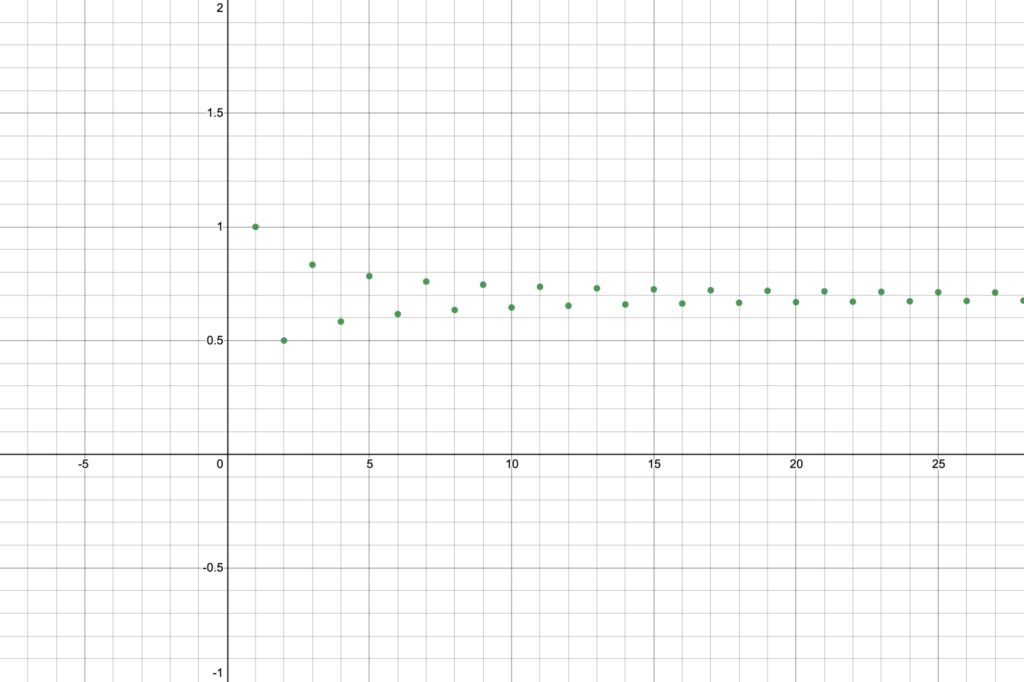
After we’ve seen Taylor Series in Lesson 20, it will be very easy for us to show that the alternating harmonic series converges to $\ln(2)$.

Alternating series test

Here are some facts to keep in mind, based on what we saw in previous lessons, in today’s Warmup exercise 1, and in today’s motivating example.

• In order for a series to even have a hope of converging, its individual terms must approach zero (consider the Divergence Test from Lesson 15).
• But just because the individual terms of a series tend to zero doesn’t mean that series will converge (consider the harmonic series $\sum_{n=1}^\infty \frac{1}{n}$…its terms approach zero, but the series still diverges).
• In our motivating example, we saw that taking a positive, decreasing series where the terms approach zero, then forming a new series by alternating the signs, gave us a new series that converged! This is the upshot of the alternating series test.

The alternating series test applies to our motivating example: the alternating harmonic series $\sum_{n=1}^\infty (-1)^{n+1} \frac{1}{n}$ because the individual terms satisfy the three conditions:

• $n > 0$ so $\frac{1}{n} > 0$ for all $n$,
• $n < n+1$ so $\frac{1}{n} > \frac{1}{n+1}$ for all $n$,
• $\lim_{n \to \infty} \frac{1}{n} = 0$.

So the alternating harmonic series $\sum_{n=1}^\infty (-1)^{n+1} \frac{1}{n}$ converges by the alternating series test.

Video 1 below shows us how to apply the alternating series test to the motivating example again, as well as to a few other examples.

Notice that if $\sum_{n=1}^\infty a_n$ is already convergent series where all the terms are positive, then the corresponding alternating series $\sum_{n=1}^\infty (-1)^n a_n$ or $\sum_{n=1}^\infty (-1)^{n+1} a_n$ will converge by the alternating series test.

Absolute and conditional convergence

If you have a series positive $\sum_{n=1}^\infty a_n$ that converges, then the corresponding alternating series $\sum_{n=1}^\infty (-1)^n a_n$ converges in a very strong sense. It “super extra converges.” That just means that it doesn’t rely on the alternating signs to converge. We want to separate this strong sense of convergence of a series from a weaker one which requires the alternating signs.

This means that there are three possibilities for any given series:

1. the series converges absolutely,
2. the series converges conditionally, or
3. the series diverges.

Example: In the case of the alternating harmonic series from our motivating example above, the series $\sum_{n=1}^\infty (-1)^{n+1}\frac{1}{n}$ converges by the alternating series test. But it does not converge absolutely because $\sum_{n=1}^\infty \frac{1}{n}$ diverges (see Lesson 15 here). Therefore, the series $\sum_{n=1}^\infty (-1)^{n+1}\frac{1}{n}$ converges conditionally. Video 2 below shows this in more detail.

The following theorem may seem obvious to you because of the language, but we still need to be explicit:

So there are two kinds of convergence (absolute and conditional) but only one kind of divergence.

Examples

Video 3 below shows the convergence (conditional or absolute) or divergence of three different series, each using different convergence tests.

Videos 4 and 5 below each show one more example of the convergence (conditional or absolute) or divergence of another series.