Boardshots
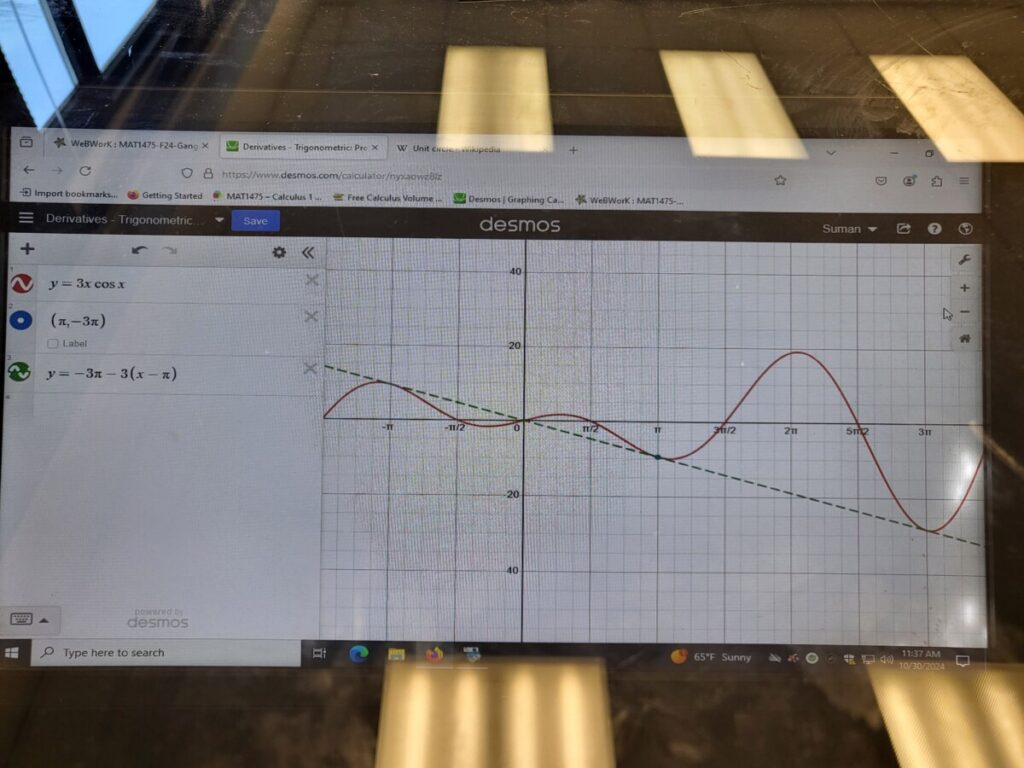
We discussed the concept of average velocity, using data from the NYC Marathon to make some calculations. I also mentioned this essay about Usain Bolt and average velocities: “Usain Bolt’s Split Times and the Power of Calculus“. We then did some more examples from the “Chain Rule – Pt 2” WebWork:


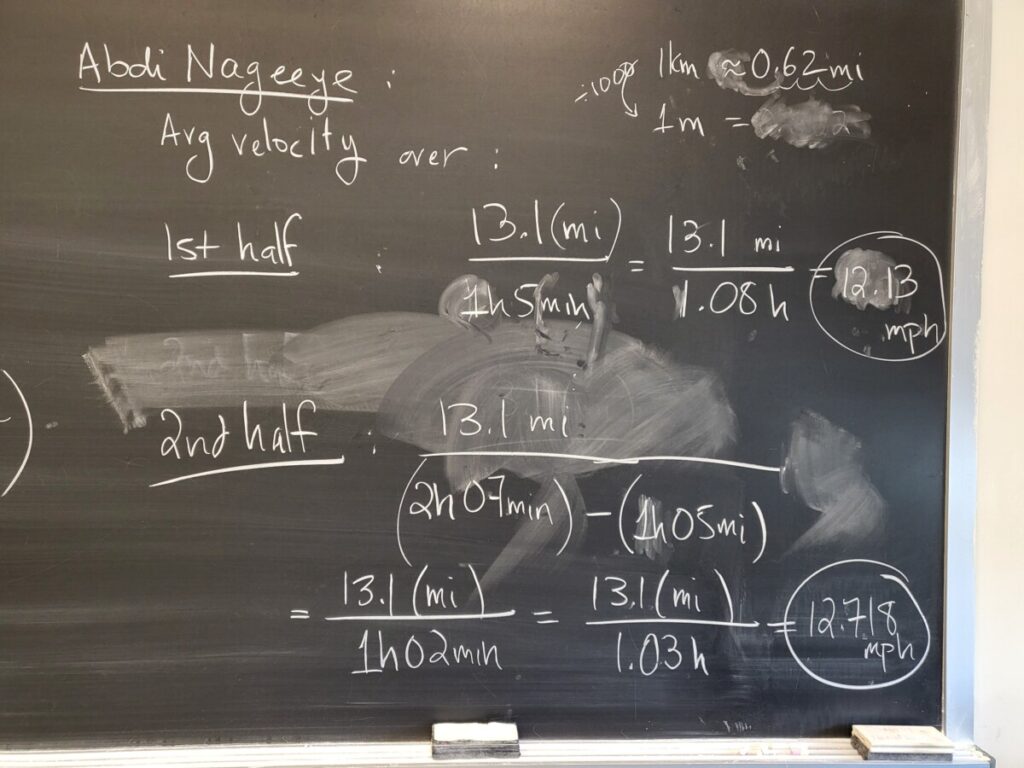
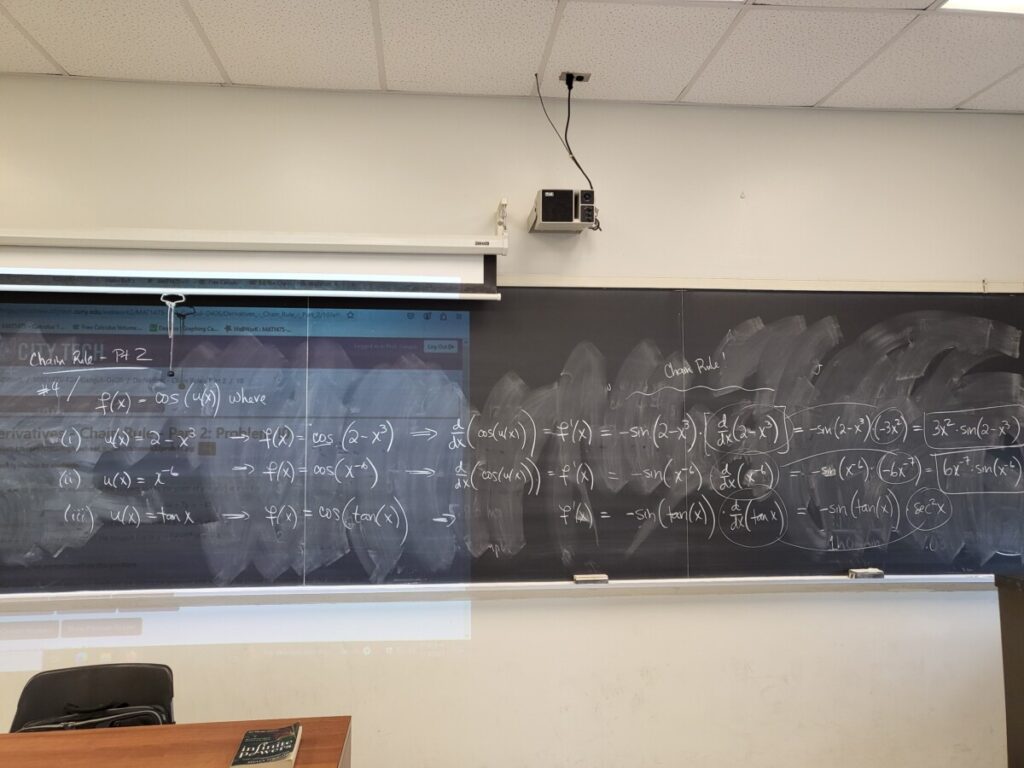
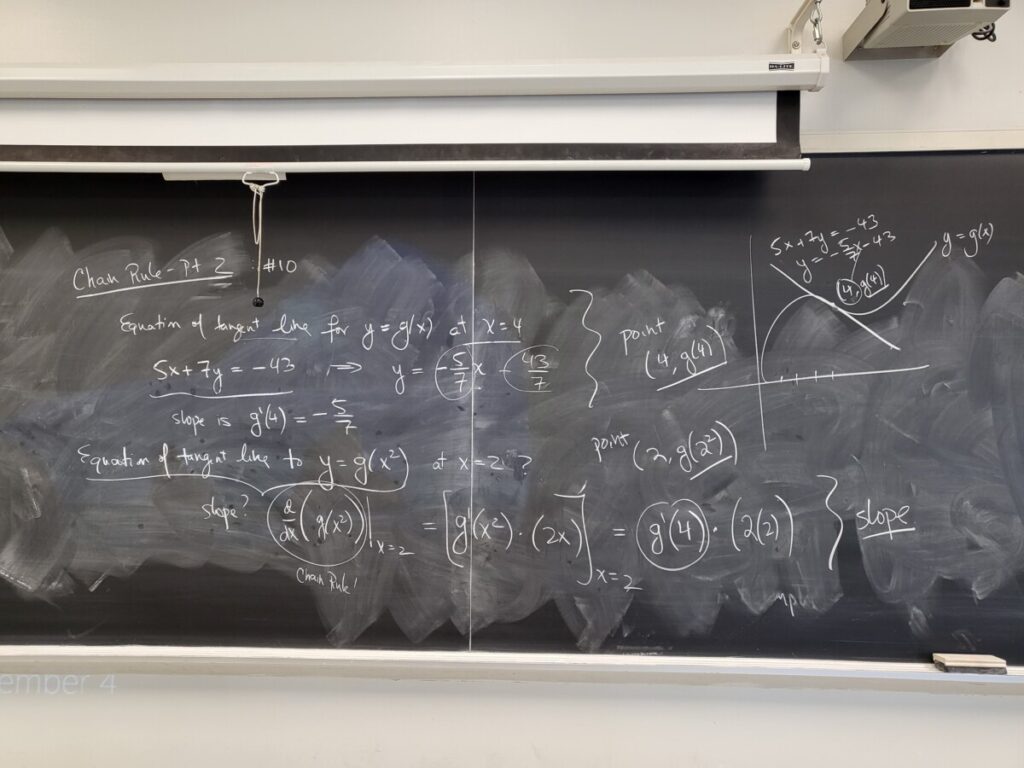




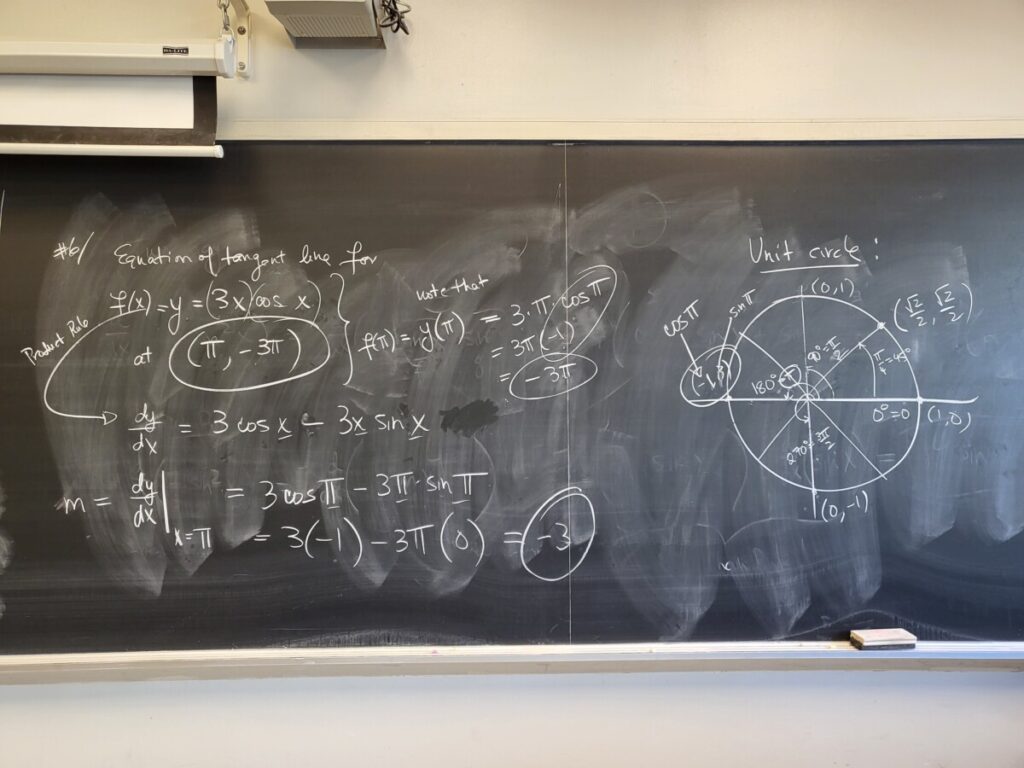
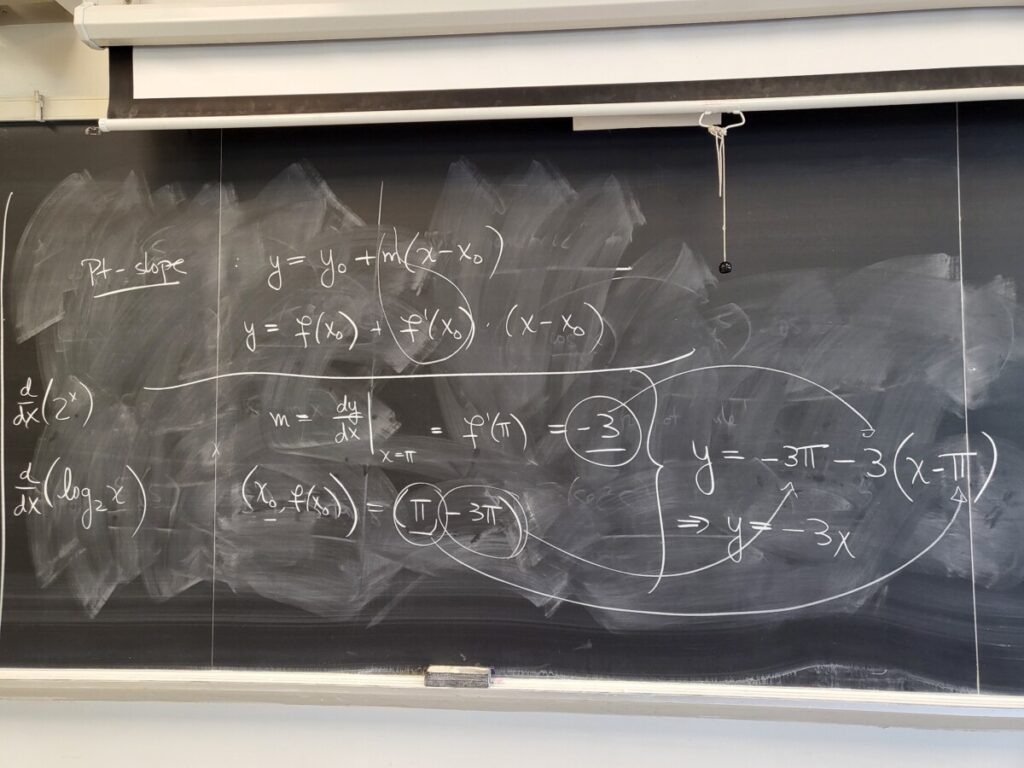
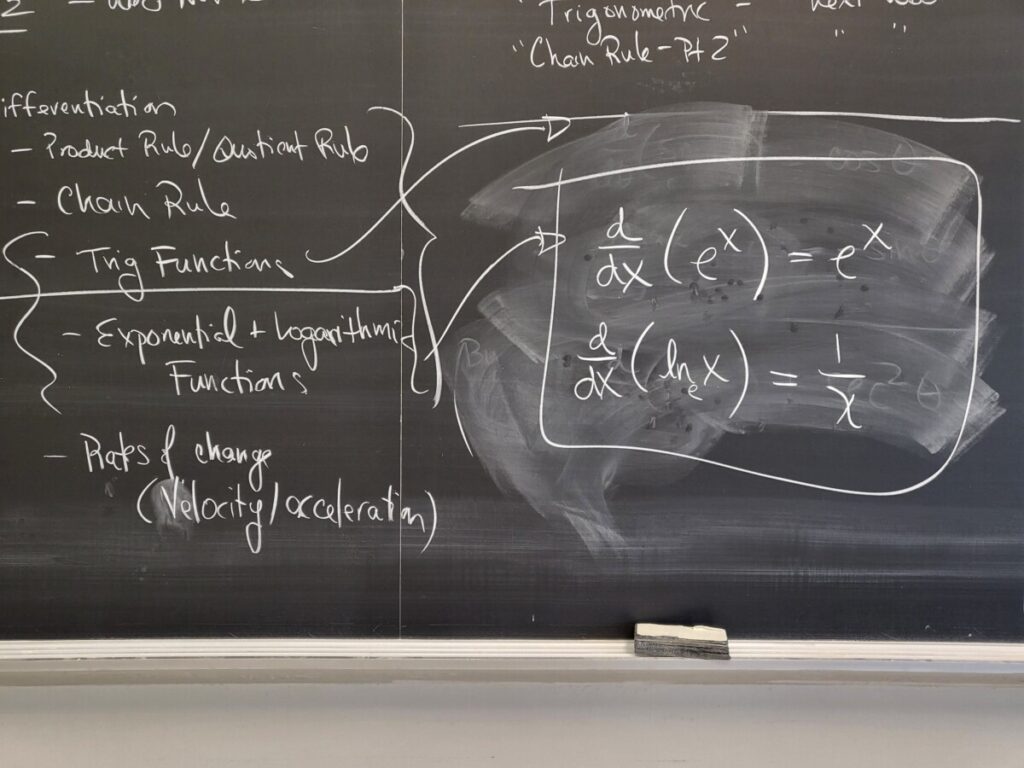


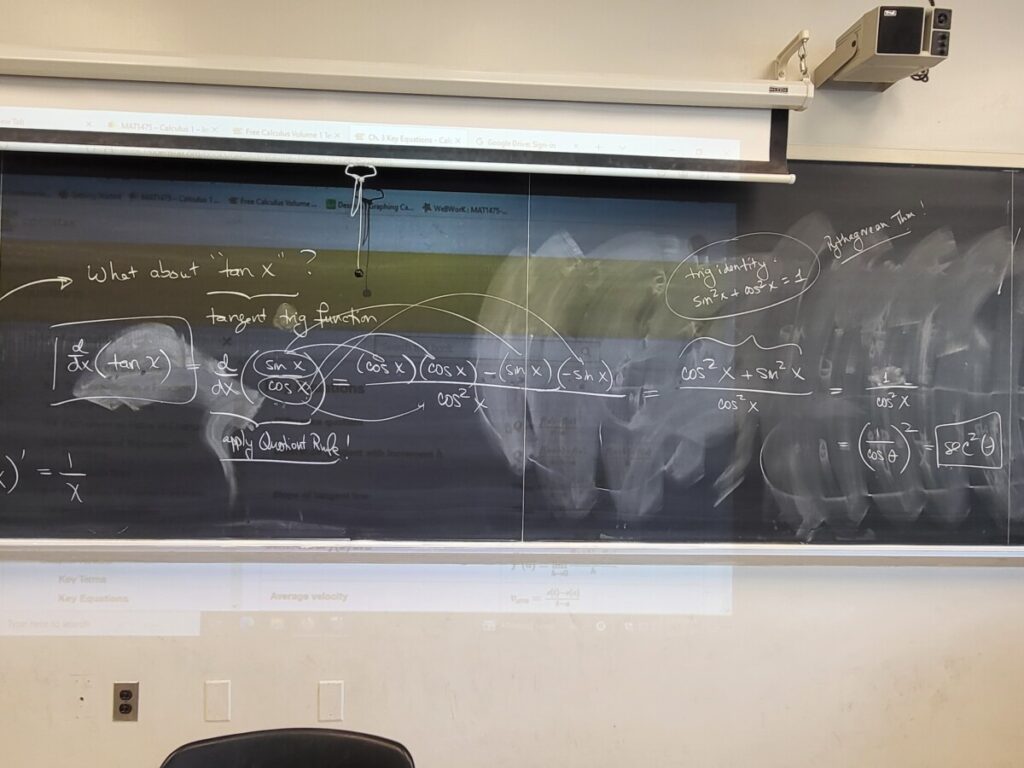
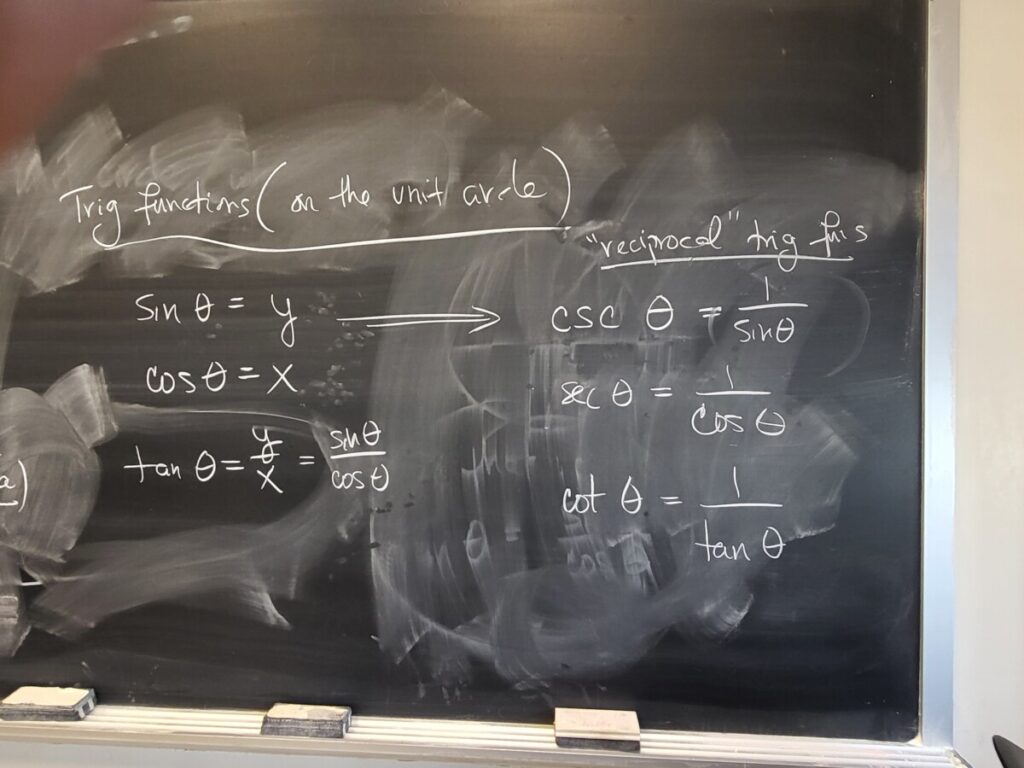



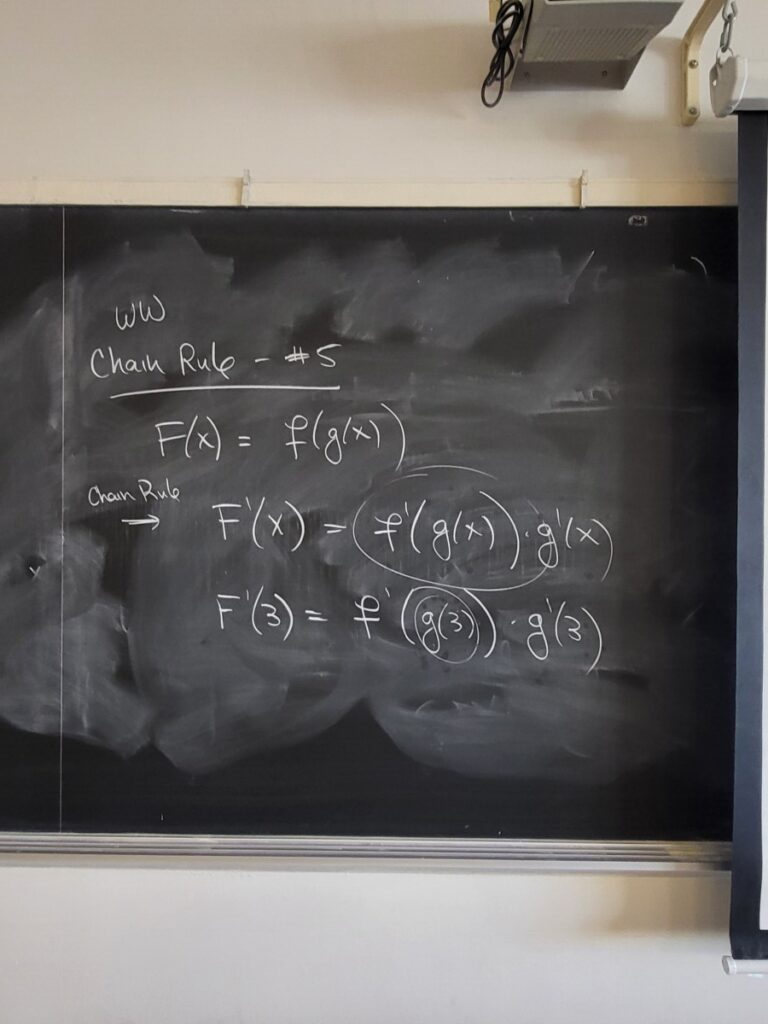

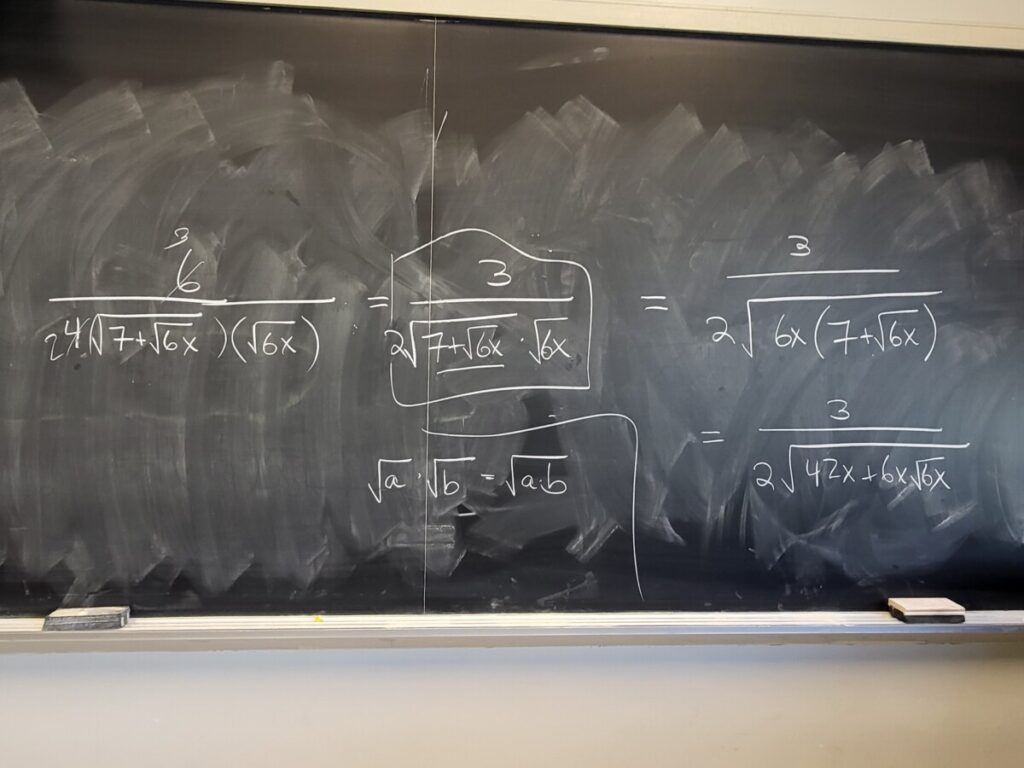

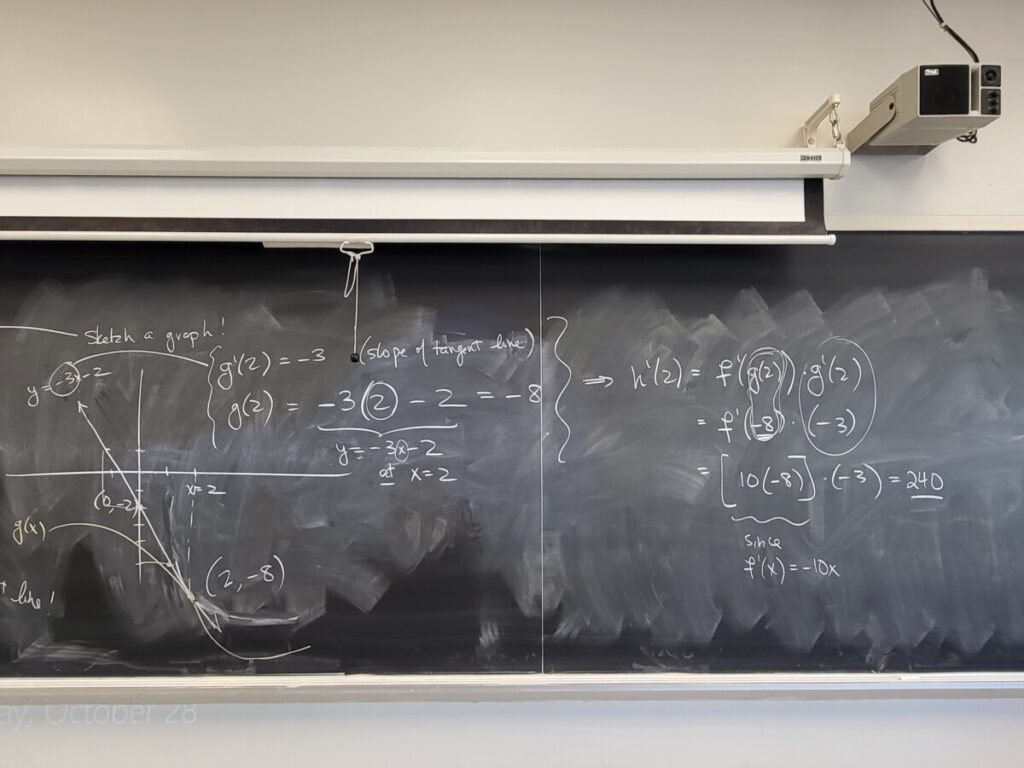



Recent Comments