Derivatives of trig functions, preview of the derivative as “instantaneous velocity”, Chain rule examples:


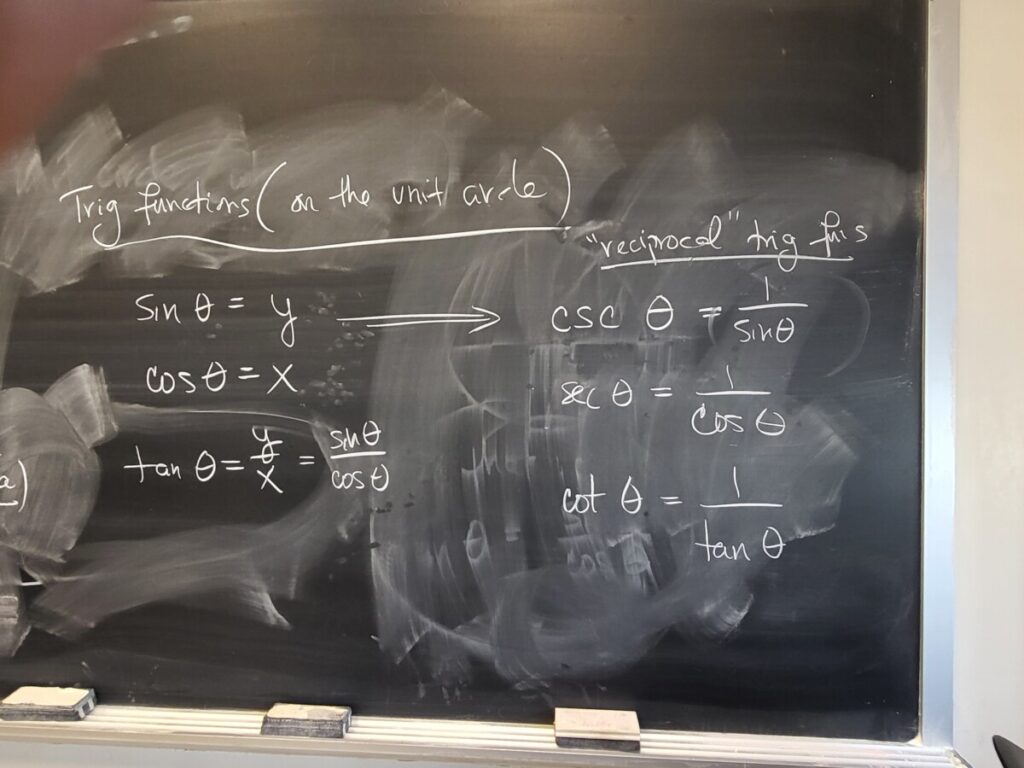



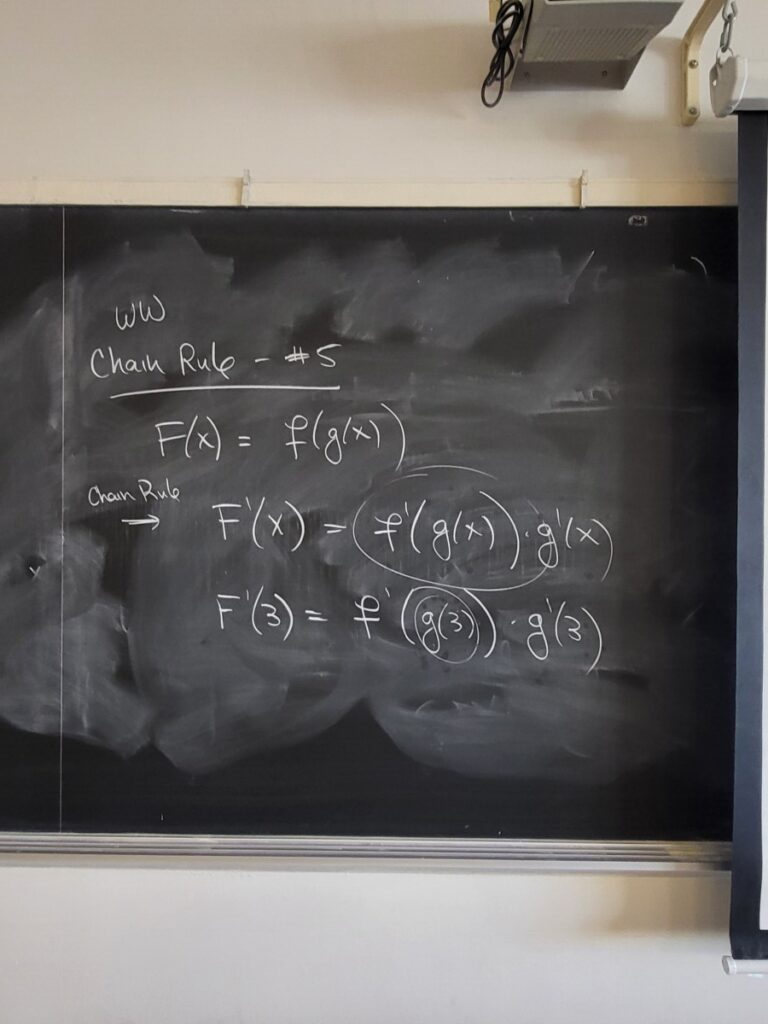

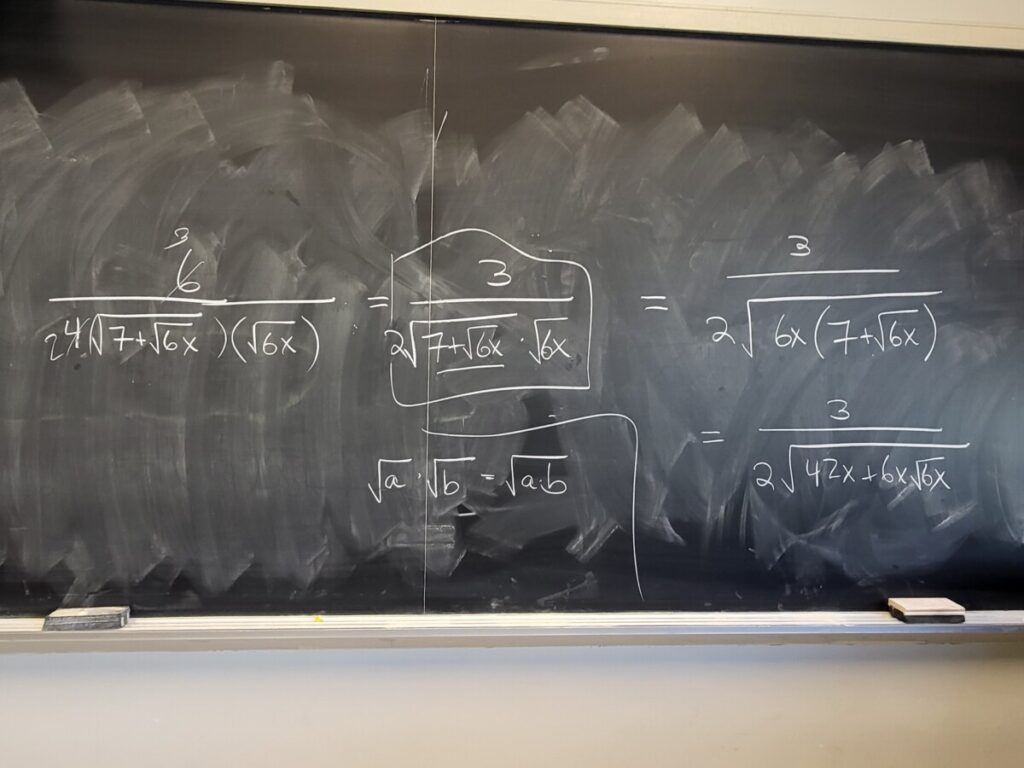

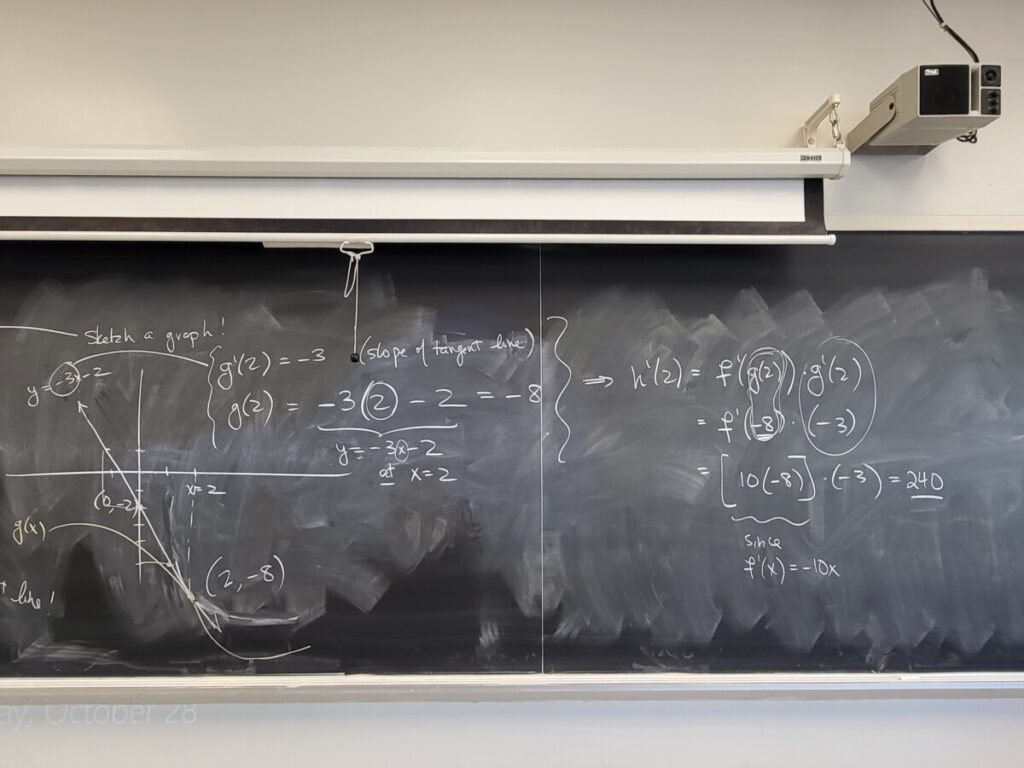
Instructor: Suman Ganguli | Fall 2024
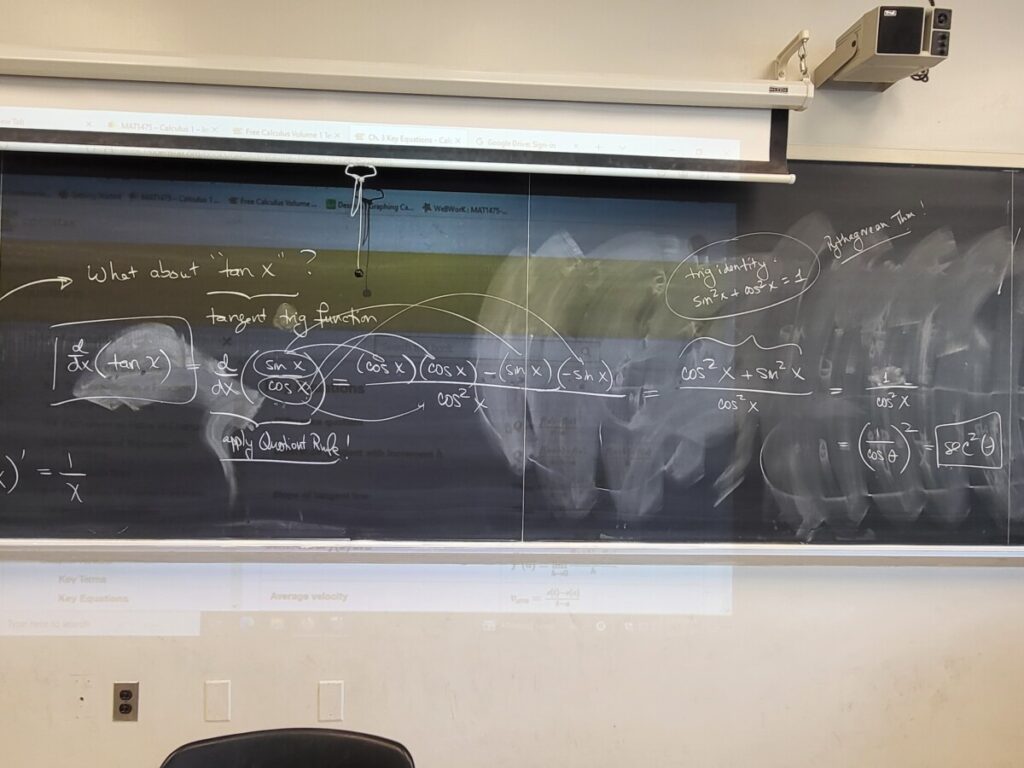
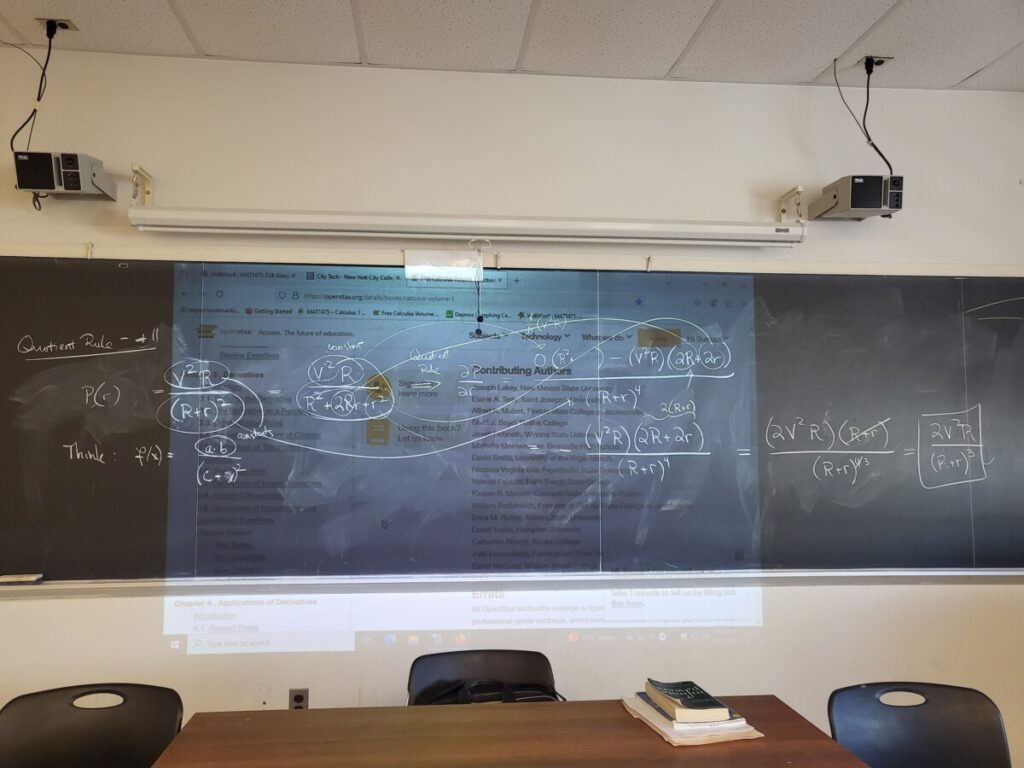
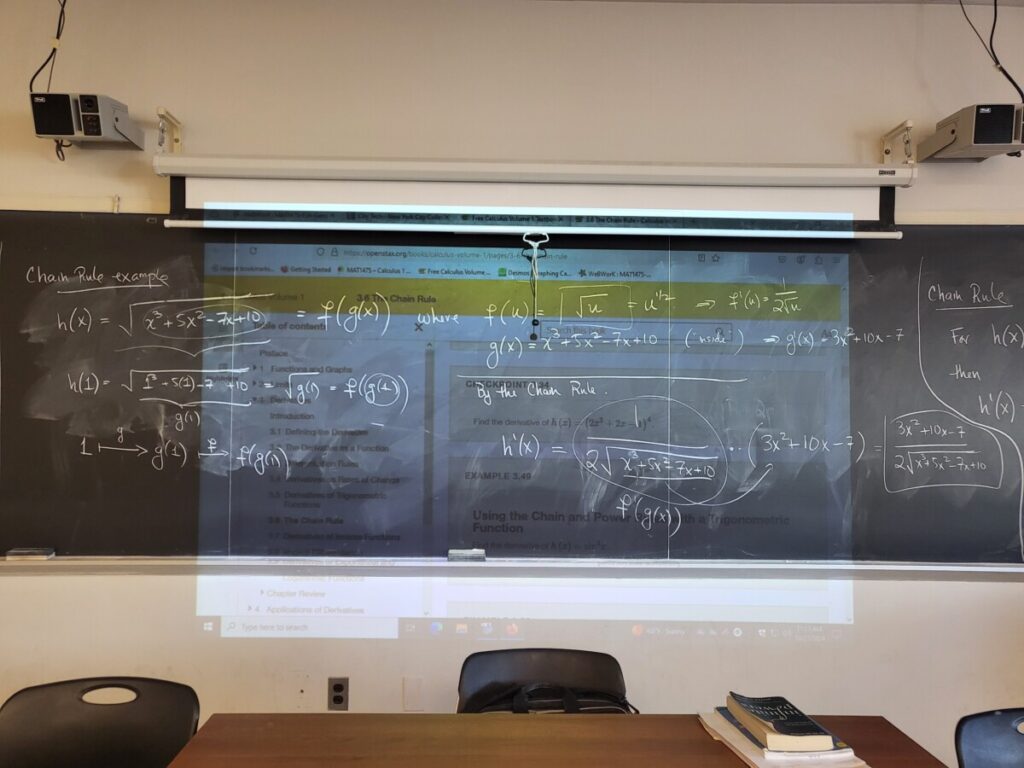
We did one more Quotient Rule example from the WebWork, and then presented the Chain Rule in more detail (Sec 3.6 of the textbook).



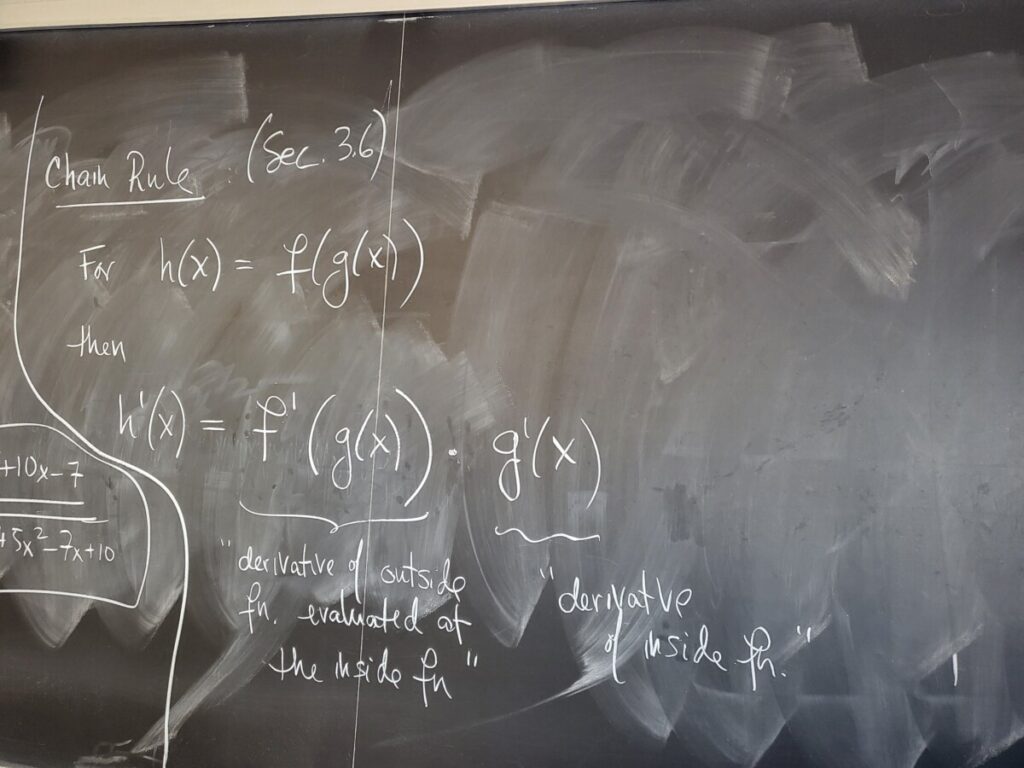

The YouTube channel/website 3blue1brown has a series of excellent videos on calculus which explain some of the topics we are covering in class.
You can watch the videos on their website, which includes additional written explanations to go with the videos–see the links below, or go to their Calculus page; or you can watch the videos via YouTube (videos embedded below).
All of these are worth watching, and will help you understand the ideas behind the techniques we are learning in class!
The paradox of the derivative:
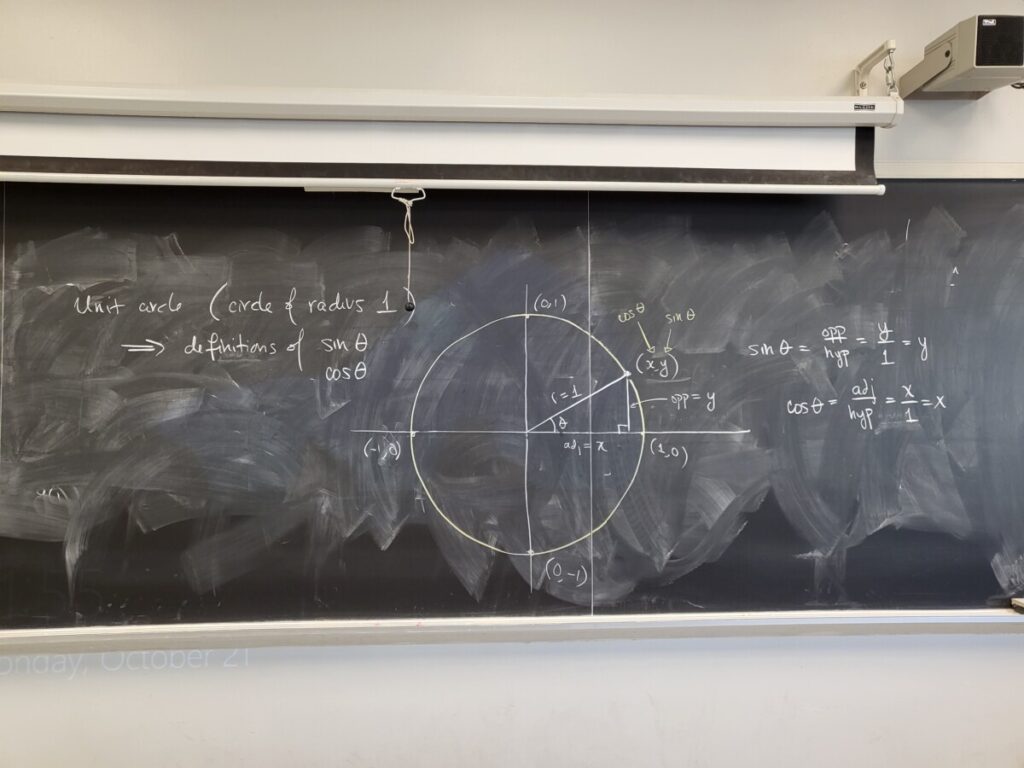
Power rule through geometry and Trig derivatives through geometry (two separate lessons on their website, covering the following video):
Visualizing the chain rule and product rule:
© 2025 MAT1475 – Calculus 1
Theme by Anders Noren — Up ↑
Recent Comments