Schedule
- WebWork: “Derivatives – Logarithmic” and “Derivatives – Implicit” extended to Fri Dec 13
- Final Exam Review: hand in written solutions to the following exercises on Wed Dec 11:
- #5 (logarithmic differentiation)
- #7 (implicit differentiation)
- #8 (tangent lines, linear approximations and differentials)
- #16 & #17 (optimization)
- #18 (using critical pts, intervals of increasing/decreasing, and intervals of concavity for sketching a graph)
- note that we will cover linear approximation/differentials and optimization on Monday, including setting up the exercises above
- we have covered logarithmic differentiation, implicit differentiation, and the concepts of #18 — please complete those now
- the Final Exam Review is available as a pdf on OpenLab Files
- Exam #3:
- take-home exercises for this exam will be handed out in class on Wed Dec 11, to be handed in on Monday Dec 16
- there will also be a short in-class exam on Monday Dec 16, similar to the take-home exercises
- we will use half the class period on Mon Dec 16 to do some additional review for the final
- Final exam: Wednesday Dec 18
Boardshots
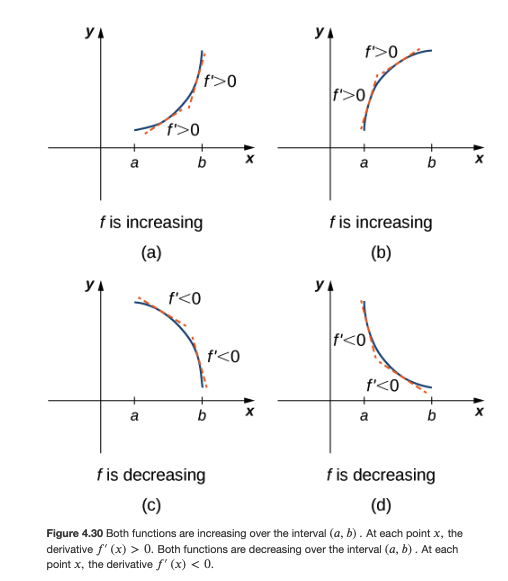
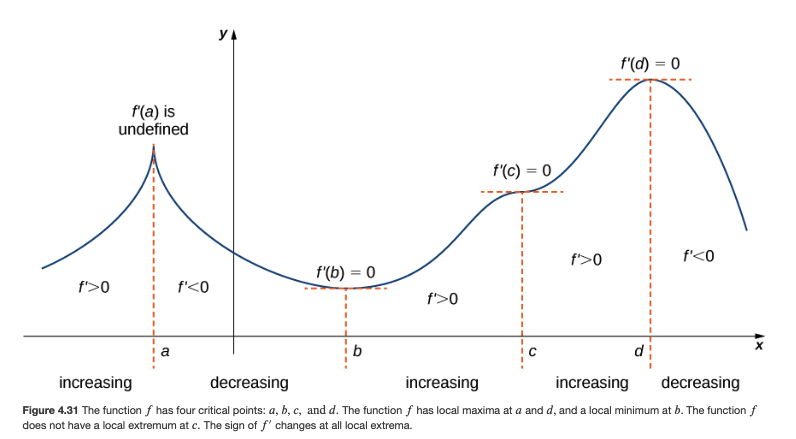
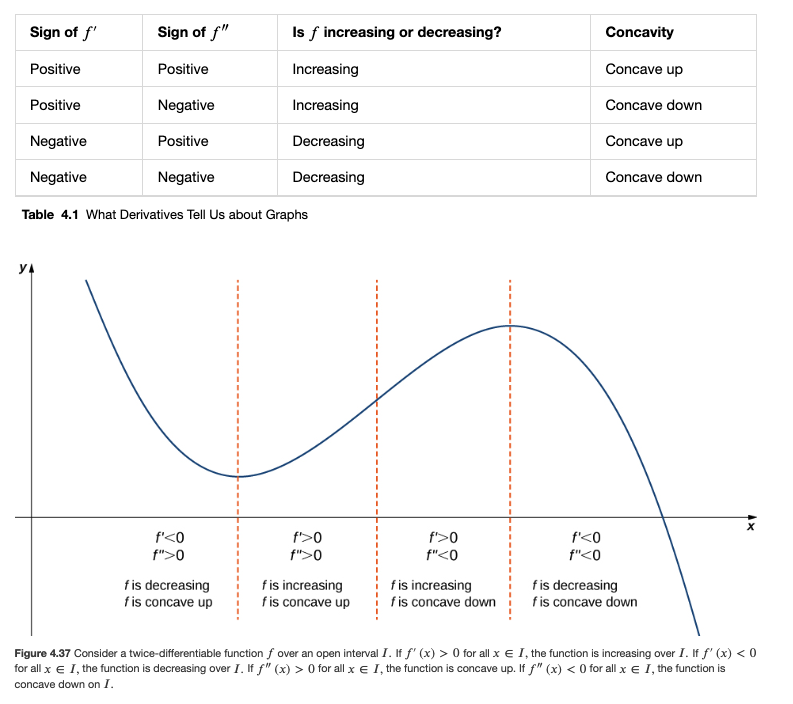
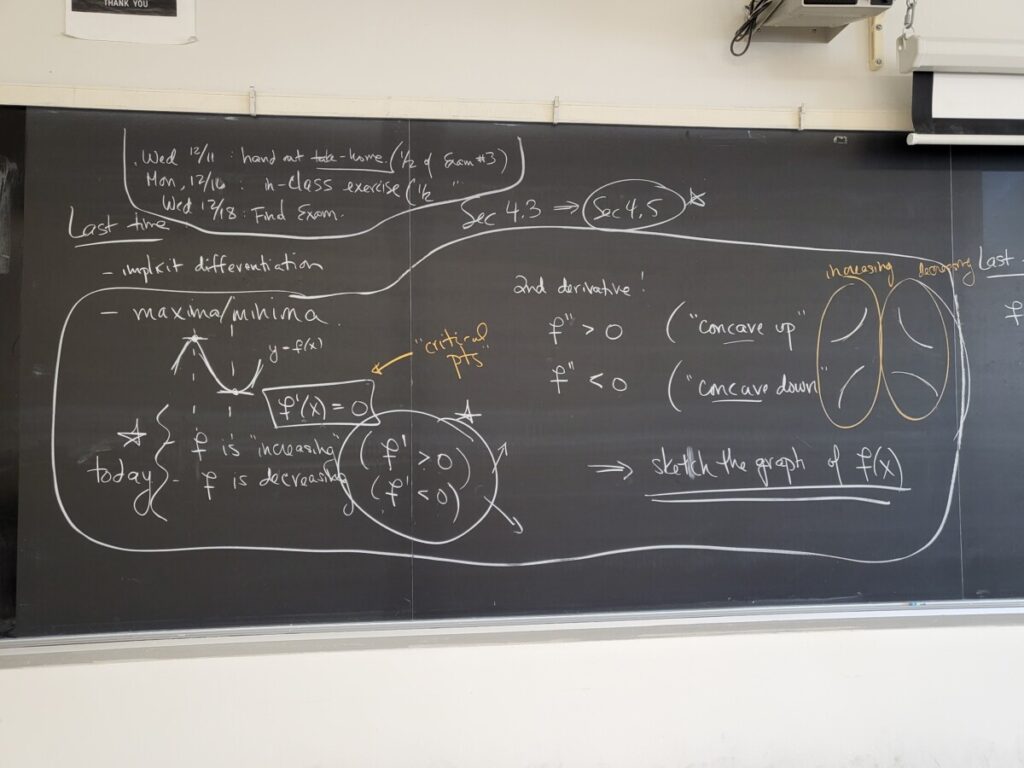
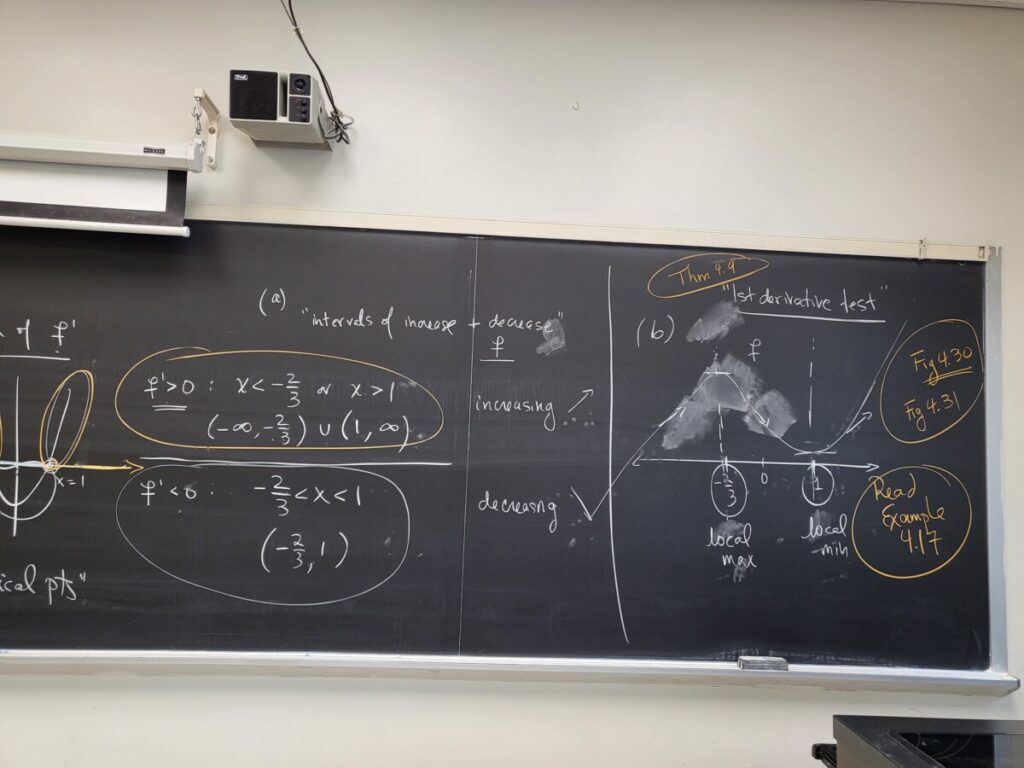
We continued the example from the previous class on graph-sketching using the first and second derivatives, looking at a cubic polynomial f(x):
- using the first derivative f'(x) to
- find the critical points (where f'(x) = 0)
- to figure out the intervals on which f(x) is increasing (which corresponds to where f'(x) > 0) vs the intervals on which f(x) is decreasing (where f'(x) < 0)
- to classify each critical point as a local max or a local min
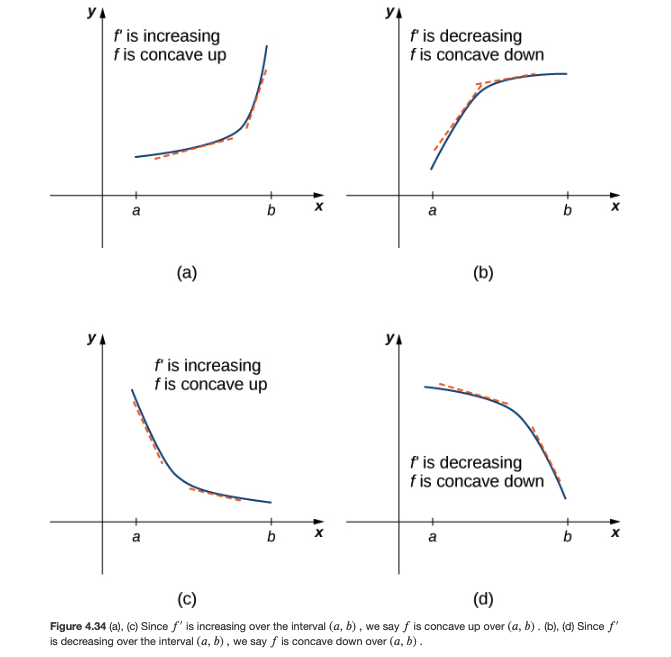
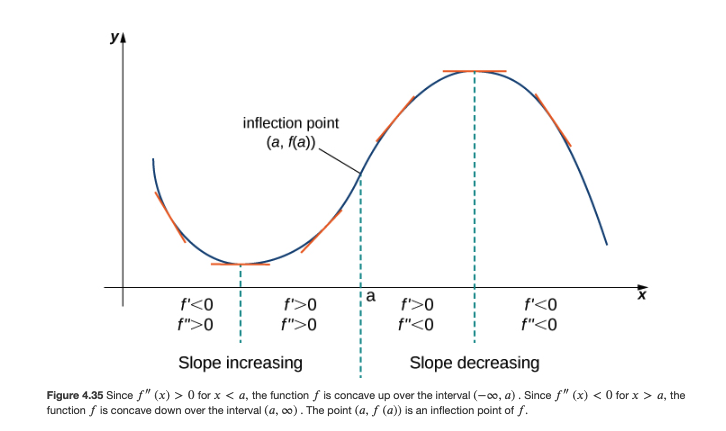
- using the second derivative f”(x) to
- figure out the intervals on which f(x) is “concave up” (where f”(x) > 0) vs the intervals on which f(x) is “concave down” (where f”(x) < 0)
- to find the inflection points (where the graph changes concavity)
- using this information to sketch the graph
Please look at the various figures in Sec 4.5 which illustrate these concepts:






0 Comments
1 Pingback