HW#1:
HW#1 will be due next Wednesday (Sept 11). Please write out the solutions to the following exercises from the OpenStax textbook on paper and hand them in on Wednesday:

Topics
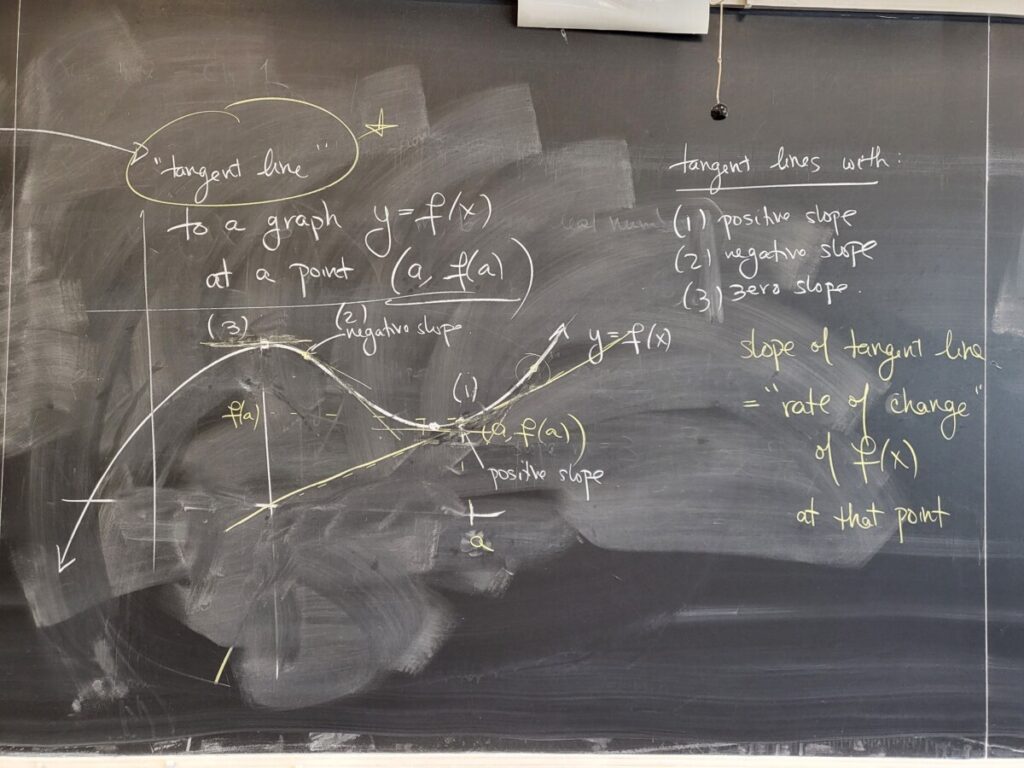
We continued discussing the main topic of Calculus 1–how to find the “steepness” or “rate of change” of a nonlinear function (curve) at a given point (a, f(a)). This material is discussed in the first half of Sec 2.1 of the textbook:
https://openstax.org/books/calculus-volume-1/pages/2-1-a-preview-of-calculus
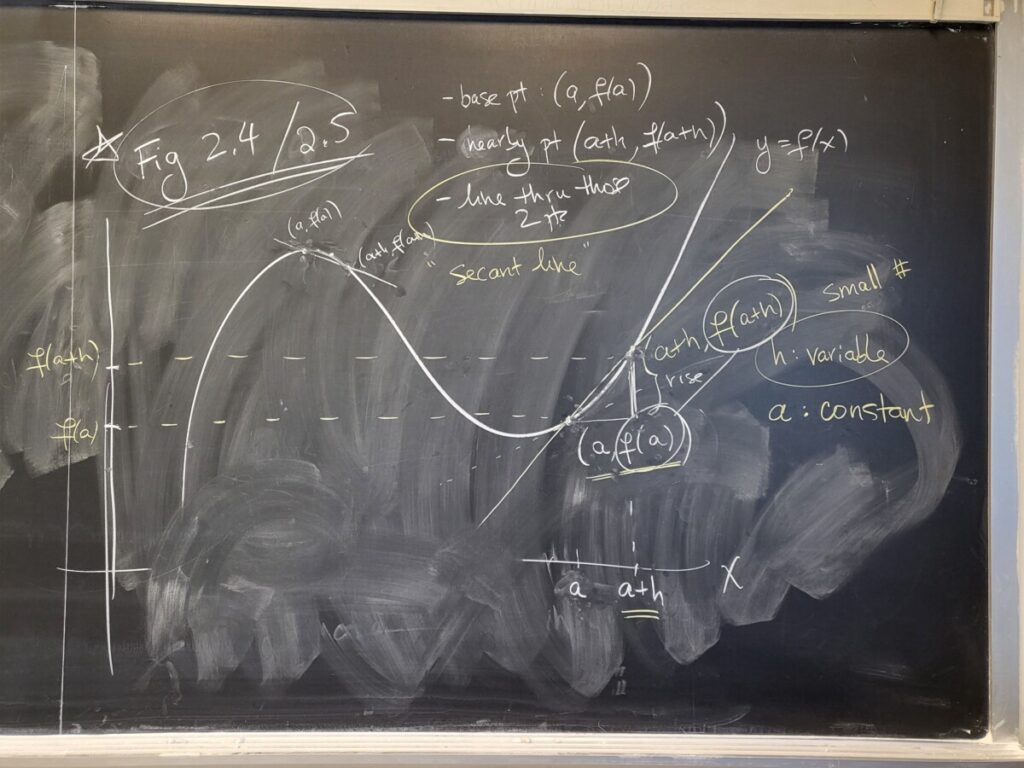
The steepness/rate of change of a function f(x) at (a, f(a)) is the slope of the tangent line to the curve at the point. We discussed how we can approximate the slope of the tangent line as the slope of a “secant line”–a line through the given point (a, f(a)) and a “closeby” point (a+h, f(a+h)). The slope of the secant line is given by a difference quotient (rise over run). This is what’s shown in Figures 2.4 and 2.5 in the textbook:
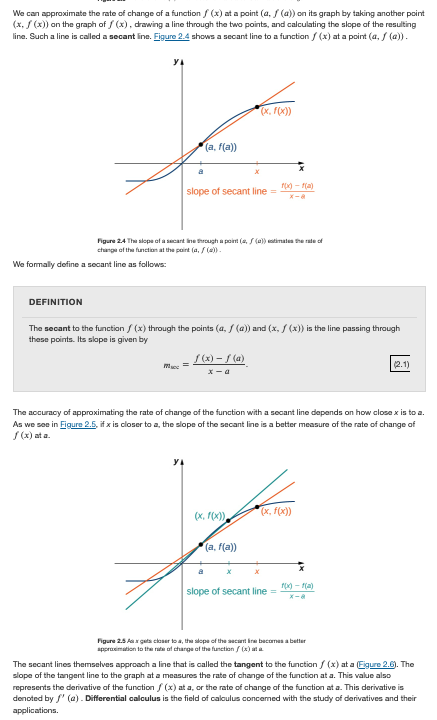
In order to get the slope of the tangent line, we calculate what happens to this different quotient as h “goes to 0” (i.e., gets closer and closer to 0)–this is called “taking the limit as h goes to 0.”
This quantity is what’s called the derivative of f(x) at x=a, denoted f'(a).
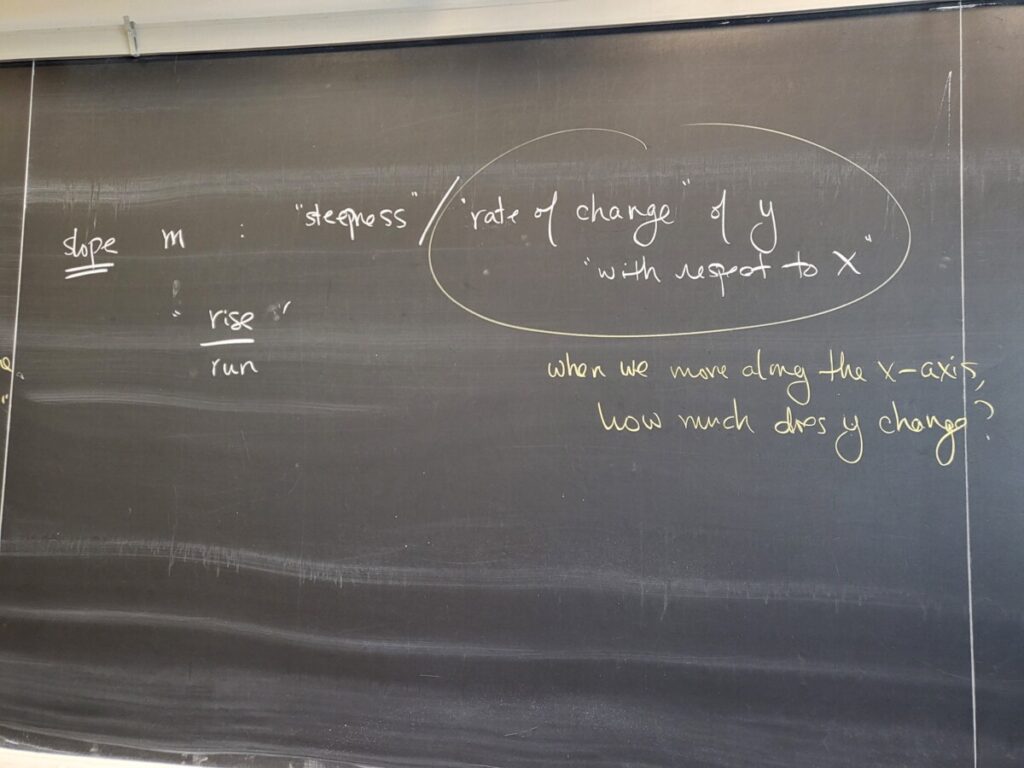


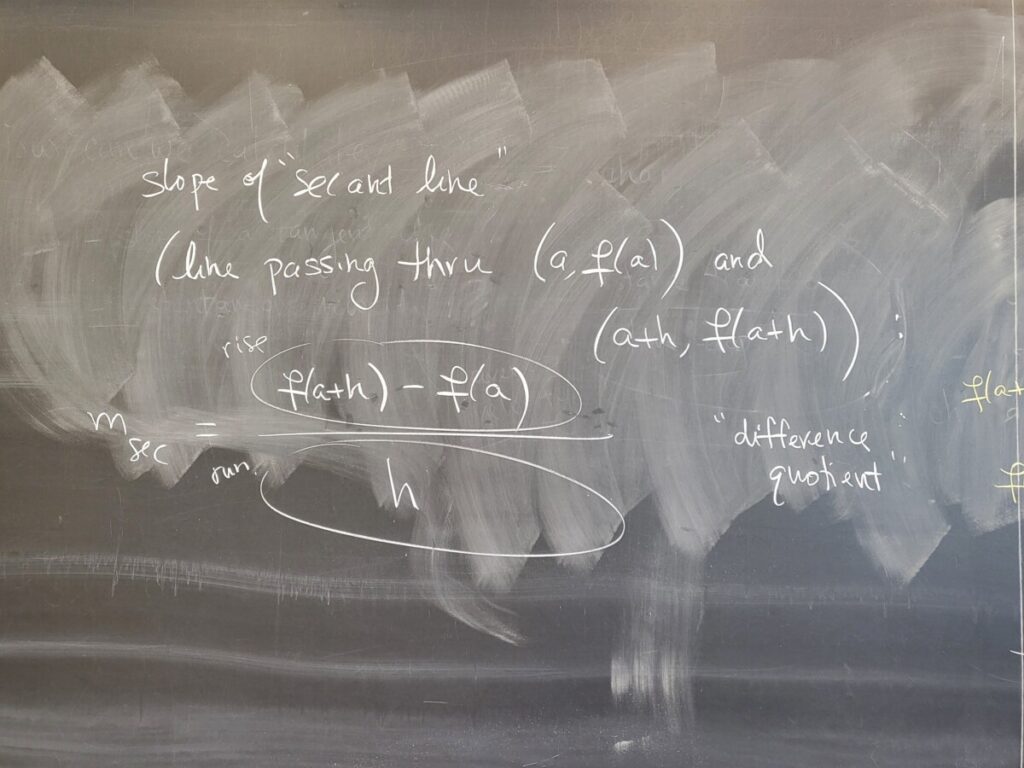


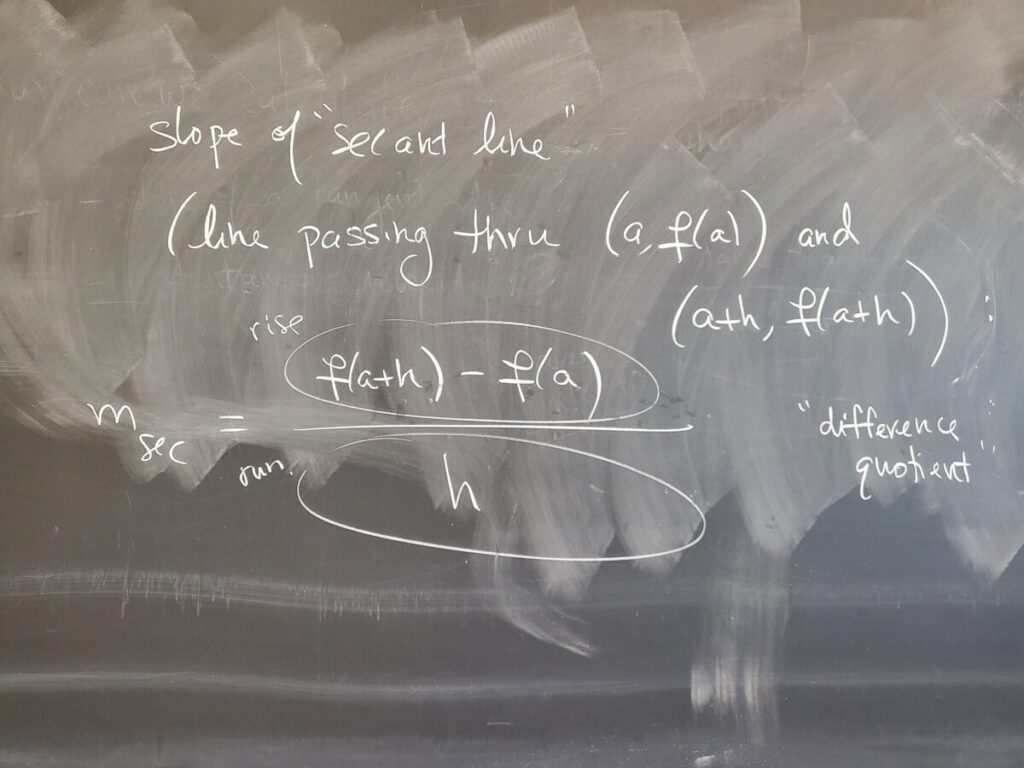



Recent Comments