Hi everyone! Read through the material below, watch the videos.
Lesson 21: Complex Numbers
Topic: This lesson covers Chapter 21: Complex numbers.
WeBWorK: There are four WeBWorK assignments on today’s material:
Complex Numbers – Operations
Complex Numbers – Magnitude
Complex Numbers – Direction
Complex Numbers – Polar Form
Question of the Day: What is the square root of $-1$?
Lesson Notes (Notability – pdf):
This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.
Review of Complex Numbers
How do we get the complex numbers? We start with the real numbers, and we throw in something that’s missing: the square root of $-1$.
Definition 21.1. We define the imaginary unit or complex unit to be:
$$i=\sqrt{-1}$$
The most important property of $i$ is: $\quad i^2=-1$
Definition 21.2. A complex number is a number of the form $a+bi$.
$a$ and $b$ are allowed to be any real numbers. $a$ is called the real part of $a+bi$, and $b$ is called the imaginary part of $a+bi$. The complex numbers are referred to as $\mathbb{C}$ (just as the real numbers are $\mathbb{R}$.
We can picture the complex number $a+bi$ as the point with coordinates $(a,b)$ in the complex plane.
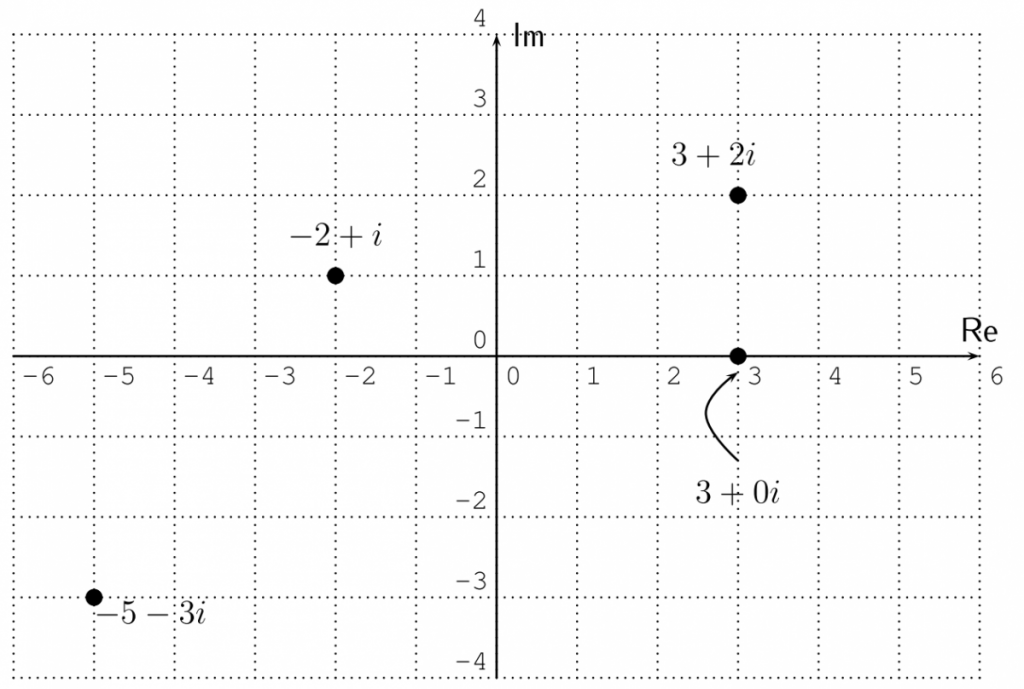
Example 21.3. Perform the operation.
a) $(2-3 i)+(-6+4 i)$
b) $(3+5 i) \cdot(-7+i)$
c) $\frac{5+4 i}{3+2 i}$
VIDEO: Review of Complex Numbers – Example 21.3
Polar form
Next, we will look at how we can describe a complex number slightly differently – instead of giving the $x$ and $y$ coordinates, we will give a distance $r$ (the modulus) and angle $\theta$ (the argument). We call this the polar form of a complex number.
Many amazing properties of complex numbers are revealed by looking at them in polar form! Let’s learn how to convert a complex number $a+bi$ into polar form, and back again.
Definition 21.4. Let $a+bi$ be a complex number. The absolute value of $a+bi$, denoted by $|a+bi|$, is the distance between the point $a+bi$ in the complex plane and the origin $(0,0)$. By the Pythagorean Theorem, we can calculate the absolute value of $a+bi$ as follows:
$$ |a+bi|=\sqrt{a^2+b^2}$$
Definition 21.6. Let $a+bi$ be a complex number. The coordinates in the plane can be expressed in terms of the absolute value, or modulus, $r=|a+bi|$ and the angle, or argument, $\theta$ formed with the positive real axis (the $x$-axis) as shown in the diagram:
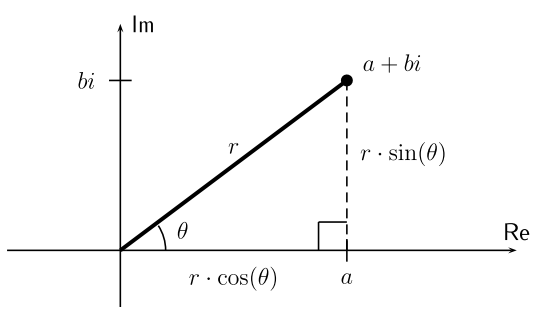
As shown in the diagram, the coordinates $a$ and $b$ are given by:
$a=r\cdot\cos(\theta), \text{ and } b=r\cdot\sin(\theta)$
Substituting and factoring out $r$, we can use these to express $a+bi$ in polar form:
Polar form: $a+bi = r\left(\cos(\theta) + i\cdot\sin(\theta)\right)$
How do we find the modulus $r$ and the argument $\theta$?
Note that $r$ is given by the absolute value. For $\theta$, we note that $\frac{b}{a}=\frac{r \cdot \sin (\theta)}{r \cdot \cos (\theta)}=\frac{\sin (\theta)}{\cos (\theta)}=\tan (\theta)$. This leads to the following:
Formulas for converting to polar form (finding the modulus $r$ and argument $\theta$): $r=\sqrt{a^2+b^2}$, $\tan(\theta)=\frac{b}{a}$
With regards to the modulus $\theta$, we can certainly use the inverse tangent function $\arctan\left(\frac{b}{a}\right)$. However, we have to be a little careful: since the arctangent only gives angles in Quadrants I and II, we need to doublecheck the quadrant of $(a,b)$.
If $\arctan\left(\frac{b}{a}\right)$ is in the correct quadrant then $\theta=\arctan\left(\frac{b}{a}\right)$. If not, then we add $\pi$ radians or $180^\circ$ to obtain the angle in the opposing quadrant: $\theta=\arctan\left(\frac{b}{a}\right)+\pi$, or $\theta=\arctan\left(\frac{b}{a}\right)+180^\circ$. You’ll see this in action in the following example.
Example 21.7. Convert the complex number to polar form.
a) $2+3 i$
b) $-2-2 \sqrt{3} i$
c) $4-3 i$
d) $-4 i$
VIDEO: Converting complex numbers to polar form – Example 21.7
Example 21.8. Convert the number from polar form into the standard form $a+bi$
a) $3 \cdot\left(\cos \left(117^{\circ}\right)+i \sin \left(117^{\circ}\right)\right)$
b) $4 \cdot\left(\cos \left(\frac{5 \pi}{4}\right)+i \sin \left(\frac{5 \pi}{4}\right)\right)$
VIDEO: Converting complex numbers from polar form into standard form – Example 21.8
Multiplication and division of complex numbers in polar form
Why is polar form useful? The primary reason is that it gives us a simple way to picture how multiplication and division work in the plane. The proposition below gives the formulas, which may look complicated – but the idea behind them is simple, and is captured in these two slogans:
When we multiply complex numbers: we multiply the $r$s and add the $\theta$s.
When we divide complex numbers: we divide the $r$s and subtract the $\theta$s
Proposition 21.9. Let $r_{1}\left(\cos \left(\theta_{1}\right)+i \sin \left(\theta_{1}\right)\right)$ and $r_{2}\left(\cos \left(\theta_{2}\right)+i \sin \left(\theta_{2}\right)\right)$ be two complex numbers in polar form. Then, the product and quotient of these are given by
$r_{1}\left(\cos \left(\theta_{1}\right)+i \sin \left(\theta_{1}\right)\right) \cdot r_{2}\left(\cos \left(\theta_{2}\right)+i \sin \left(\theta_{2}\right)\right) \ =r_{1} r_{2} \cdot\left(\cos \left(\theta_{1}+\theta_{2}\right)+i \sin \left(\theta_{1}+\theta_{2}\right)\right)$
$\frac{r_{1}\left(\cos \left(\theta_{1}\right)+i \sin \left(\theta_{1}\right)\right)}{r_{2}\left(\cos \left(\theta_{2}\right)+i \sin \left(\theta_{2}\right)\right)} =\frac{r_{1}}{r_{2}} \cdot\left(\cos \left(\theta_{1}-\theta_{2}\right)+i \sin \left(\theta_{1}-\theta_{2}\right)\right)$
Example 21.10. Multiply or divide the complex numbers, and write your answer in polar and standard form.
a) $5\left(\cos \left(11^{\circ}\right)+i \sin \left(11^{\circ}\right)\right) \cdot 8\left(\cos \left(34^{\circ}\right)+i \sin \left(34^{\circ}\right)\right)$
b) $\quad 3\left(\cos \left(\frac{5 \pi}{8}\right)+i \sin \left(\frac{5 \pi}{8}\right)\right) \cdot 12\left(\cos \left(\frac{7 \pi}{8}\right)+i \sin \left(\frac{7 \pi}{8}\right)\right)$
c) $\frac{32\left(\cos \left(\frac{\pi}{4}\right)+i \sin \left(\frac{\pi}{4}\right)\right)}{8\left(\cos \left(\frac{7 \pi}{12}\right)+i \sin \left(\frac{7 \pi}{12}\right)\right)}$
d) $\frac{4\left(\cos \left(203^{\circ}\right)+i \sin \left(203^{\circ}\right)\right)}{6\left(\cos \left(74^{\circ}\right)+i \sin \left(74^{\circ}\right)\right)}$
e) INTUITIVE BONUS: Without doing any calculation or conversion, describe where in the complex plane to find the number obtained by multiplying $(5+2i)(-1+6i)$.
VIDEO: Multiplication and division of complex numbers in polar form – Example 21.10
That’s it for today! Give the WeBWorK a try.
Print this page


0 Comments
1 Pingback