Welcome MAT 1375 Faculty! This Course Hub is intended as a central repository of resources for the course. Announcements for all faculty teaching the course will be posted here.
Author: Jonas Reitz (Page 1 of 2)
Hi everyone! Read through the material below, watch the videos.
Lesson 24: The geometric series
Topic: This lesson covers Chapter 24: The geometric series
WeBWorK: There are two WeBWorK assignments on today’s material:
Sequences – Geometric
Series – Geometric
Question of the day: Can we add up infinitely many numbers?
Lesson Notes (Notability – pdf):
This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.
Finite geometric series
Today we look at a new kind of sequence, called a geometric sequence, and the corresponding series, geometric series.
A geometric sequence is a sequence for which we multiply by a constant number to get from one term to the next, for example:

Definition 24.1. A sequence $\left\{a_{n}\right\}$ is called a geometric sequence, if any two consecutive terms have a common ratio $r$. The geometric sequence is determined by $r$ and the first value $a_{1}$. This can be written recursively as:
$$a_{n}=a_{n-1} \cdot r \quad \text { for } n \geq 2$$
Alternatively, we have the general formula for the $n$ th term of the geometric sequence:
$$a_{n}=a_{1} \cdot r^{n-1}$$
Example 24.2. Determine if the sequence is a geometric or arithmetic sequence, or neither or both. If it is a geometric or arithmetic sequence, then find the general formula.
a) $3,6,12,24,48, \dots$
b) $100,50,25,12.5, \ldots$
c) $700,-70,7,-0.7,0.07, \ldots$
d) $2,4,16,256, \dots$
e) $3,10,17,24, \ldots$
f) $\quad-3,-3,-3,-3,-3, \dots$
g) $a_{n}=\left(\frac{3}{7}\right)^{n}$
h) $a_{n}=n^{2}$
VIDEO: Introduction to geometric sequences, Example
Example 24.3. Find the general formula of a geometric sequence with the given property
a) $r=4,$ and $a_{5}=6400$
b) $a_{1}=\frac{2}{5},$ and $a_{4}=-\frac{27}{20}$
c) $a_{5}=216, a_{7}=24,$ and $r$ is positive
VIDEO: Finding the formula of a geometric sequence – Example 24.3
Example 24.4. Consider the geometric sequence $a_{n}=8 \cdot 5^{n-1},$ that is the sequence:
$$8,40,200,1000,5000,25000,125000, \ldots$$
Find the sum of the first 6 terms of this sequence
$$8+40+200+1000+5000+25000=31248$$
VIDEO: Sum of a geometric series – intro example
Observation 24.5. Let $\left\{a_{n}\right\}$ be a geometric sequence, whose $n$ th term is given by the formula $a_{n}=a_{1} \cdot r^{n-1} .$ We furthermore assume that $r \neq 1 .$ Then, the sum $a_{1}+a_{2}+\dots+a_{k-1}+a_{k}$ is given by
$$\sum_{i=1}^{k} a_{i}=a_{1} \cdot \frac{1-r^{k}}{1-r}$$
Example 24.6. Find the value of the geometric series.
a) Find the sum $\sum_{n=1}^{6} a_{n}$ for the geometric sequence $a_{n}=10 \cdot 3^{n-1}$
b) Determine the value of the geometric series: $\sum_{k=1}^{5}\left(-\frac{1}{2}\right)^{k}$
c) Find the sum of the first 12 terms of the geometric sequence
$$-3,-6,-12,-24, \dots$$
VIDEO: The sum of a finite geometric series, Example 24.6
Infinite geometric series
Sometimes it makes sense to add up not just a finite number of terms in a sequence, but ALL the terms (infinitely many!).
Example 24.7. Consider the geometric sequence
$$1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \ldots$$
What is the initial term? What is the common ratio?
Let’s try adding up some of the terms. Try this by hand, and by using the formula for finite geometric series. What happens if we add up ALL the terms?
VIDEO: Infinite geometric series – intro example and formula
Definition 24.8. An infinite series is given by the formula
$$\sum_{i=1}^{\infty} a_{i}=a_{1}+a_{2}+a_{3}+\ldots$$
Observation 24.9. Let $\left{a_{n}\right}$ be a geometric sequence with $a_{n}=a_{1} \cdot r^{n-1}$ Then the infinite geometric series is defined whenever $-1<r<1$. In this case, we have:
$$\sum_{i=1}^{\infty} a_{i}=a_{1} \cdot \frac{1}{1-r}$$
$\quad$
Example 24.10. Find the value of the infinite geometric series.
a) $\sum_{j=1}^{\infty} a_{j},$ for $a_{j}=5 \cdot\left(\frac{1}{3}\right)^{j-1}$
b) $\sum_{n=1}^{\infty} 3 \cdot(0.71)^{n}$
c) $500-100+20-4+\ldots$
d) $3+6+12+24+48+\ldots$
Example 24.11. Consider the real number given by $0.555555\dots$. Rewrite this number as an infinite geometric series. Can you figure out what fraction it is equal to?
VIDEO: Infinite geometric series – examples
Hi everyone! Read through the material below, watch the videos!
Lesson 23: Sequences and series
Topic: This lesson covers Chapter 23: Sequences and series
WeBWorK: There are three WeBWorK assignments on today’s material:
Sequences – Introduction
Sequences – Arithmetic
Series – Finite Arithmetic
Question of the day: What is a sequence? What is a series?
Answer of the day: A sequence is just a list of numbers. A series is list of numbers, added up.
Lesson Notes (Notability – pdf):
This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.
Introduction to sequences and series
Today we will introduce two very powerful ideas (they are the building blocks of Calculus) – however, the ideas themselves are not complicated: sequences and series. They both have to do with lists of numbers, rather than individual numbers.
Definition 23.1. A sequence is an ordered list of numbers (we call each number in the list a term in the sequence). We write a sequence in order as follows: $a_{1}, a_{2}, a_{3}, a_{4},…$
In short we write the above sequence as $\left\{a_{n}\right\}$ or $\left\{a_{n}\right\}_{n \geq 1}$
Let’s look at examples of some sequences. As you look at this example, keep the following questions in mind:
- Is there a pattern in the sequence?
- Can you predict what the next term of the sequence will be?
- Can you predict what the 10th term of the sequence will be? What about the 20th, or the 100th?
- Can you find a formula for $a_n$, the $n$th term of the sequence?
Example 23.2. Here are some examples of sequences.
a) $4,6,8,10,12,14,16,18, \dots$
b) $1,3,9,27,81,243, \dots$
c) $+5,-5,+5,-5,+5,-5, \dots$
d) $1,1,2,3,5,8,13,21,34,55, \dots$
e) $5,8,-12,4,5.3,7,-3, \sqrt{2}, 18, \frac{2}{3}, 9, \dots$
Example 23.3. Consider the sequence $\left\{a_{n}\right\}$ with $a_{n}=4 n+3$. Calculate the first five terms of the sequence $a_1, a_2, a_3, a_4,$ and $a_5$. What is the $200$th term of the sequence?
VIDEO: Introduction to sequences – Examples 23.2 and 23.3
Example 23.4. Find the first 6 terms of each sequence.
a) $a_{n}=n^{2}$
b) $a_{n}=\frac{n}{n+1}$
c) $a_{n}=(-1)^{n}$
d) $a_{n}=(-1)^{n+1} \cdot 2^{n}$
Another way to describe a sequence is by giving a recursive formula for the $n$th term $a_{n}$ in terms of the lower terms. Here are some examples.
Example 23.6. Find the first $6$ terms in the sequence described below.
a) $a_{1}=4,$ and $a_{n}=a_{n-1}+5$ for $n>1$
b) $a_{1}=3,$ and $a_{n}=2 \cdot a_{n-1}$ for $n>1$
c) $a_{1}=1, a_{2}=1,$ and $a_{n}=a_{n-1}+a_{n-2}$ for $n>2$
VIDEO: Two ways of describing sequences -Examples 23.4 and 23.6
Definition 23.8. A series is a sum of terms in a sequence. We denote the sum of the first $k$ terms in a sequence with the following notation:
$\sum_{i=1}^{k} a_{i}=a_{1}+a_{2}+\cdots+a_{k}$
The summation symbol $\sum $ comes from the greek letter $\Sigma$, pronounced “sigma,” which is the greek letter for “S.”
Example 23.9. Find the sum.
a) $\sum_{i=1}^{4} a_{i},$ for $a_{i}=7 i+3$
b) $\sum_{j=1}^{6} a_{j},$ for $a_{n}=(-2)^{n}$
c) $\sum_{k=1}^{5}\left(4+k^{2}\right)$
VIDEO: Intro to series – Example 23.9
The arithmetic sequence
Definition 23.10. A sequence $\left{a_{n}\right}$ is called an arithmetic sequence if any two consecutive terms have a common difference $d$. The arithmetic sequence is determined by $d$ and the first value $a_{1}$. This can be written recursively as:
$a_{n}=a_{n-1}+d \quad \text { for } n \geq 2$
Alternatively, we have the general formula for the $n$th term of the arithmetic sequence
$a_{n}=a_{1}+d \cdot(n-1)$
Example 23.11. Determine if the sequence is an arithmetic sequence. If so, then find the general formula for $a_{n}$.
a) $7,13,19,25,31, \ldots$
b) $13,9,5,1,-3,-7, \dots$
c) $10,13,16,20,23, \dots$
d) $a_{n}=8 \cdot n+3$
VIDEO: Arithmetic sequences – Example 23.11
Example 23.12. Find the general formula of an arithmetic sequence with the given property.
a) $d=12,$ and $a_{6}=68$
b) $a_{1}=-5,$ and $a_{9}=27$
c) $a_{5}=38,$ and $a_{16}=115$
VIDEO: Arithmetic sequences – finding a general formula, Example 23.12
Example 23.13. Find the sum of the first 100 integers, starting from 1 . In other words, we want to find the sum of $1+2+3+\cdots+99+100$.
VIDEO: Arithmetic series – intro example 23.13
Observation 23.14 . Let $\left\{a_{n}\right\}$ be an arithmetic sequence, whose $n$ th term is given by the formula $a_{n}=a_{1}+d(n-1)$. Then, the sum $a_{1}+a_{2}+\cdots+a_{k-1}+a_{k}$ is given by adding $\left(a_{1}+a_{k}\right)$ precisely $\frac{k}{2}$ times:
$\sum_{i=1}^{k} a_{i}=\frac{k}{2} \cdot\left(a_{1}+a_{k}\right)$
Example 23.15. Find the value of the arithmetic series.
a) Find the sum $a_{1}+\cdots+a_{60}$ for the arithmetic sequence $a_{n}=2+13(n-1)$
b) Determine the value of the sum: $\quad \sum_{j=1}^{1001}(5-6 j)$
c) Find the sum of the first 35 terms of the sequence
$4,3.5,3,2.5,2,1.5, \ldots$
VIDEO: Arithmetic series – finding the sum, Example 23.15
Hi everyone! Read through the material below, watch the videos.
Lesson 22: Vectors in the plane
Topic: This lesson covers Chapter 22: Vectors in the plane.
WeBWorK: There are four WeBWorK assignments on today’s material:
Vectors – Components
Vectors – Operations
Vectors – Magnitude and Direction
Vectors – Unit Vectors
Lesson Notes (Notability – pdf):
This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.
Introduction to Vectors
Today we will be working with the plane $\mathbb{R}^2$, but looking at things in a slightly different way – instead of points (which have only a location), we will be focussing on vectors (which have a magnitude (size) and direction). This change in perspective is quite powerful, and brings to light many useful features of the plane – but in practice, you will find it similar to the work we did in the previous lesson on polar form of complex numbers.
Definition 22.1. A geometric vector in the plane is a geometric object in the plane $\mathbb{R}^{2}$ that is given by a direction (angle) and magnitude (size). We denote a vector by $\vec{v}$ (it is written by some authors as $v$ ), its magnitude is denoted by $||\vec{v}||,$ and its directional angle by $\theta$.
Vectors are often drawn as directed line segments $\vec{v}=\overrightarrow{P Q}$. Two such segments represent the same vector if they have the same magnitude and direction.
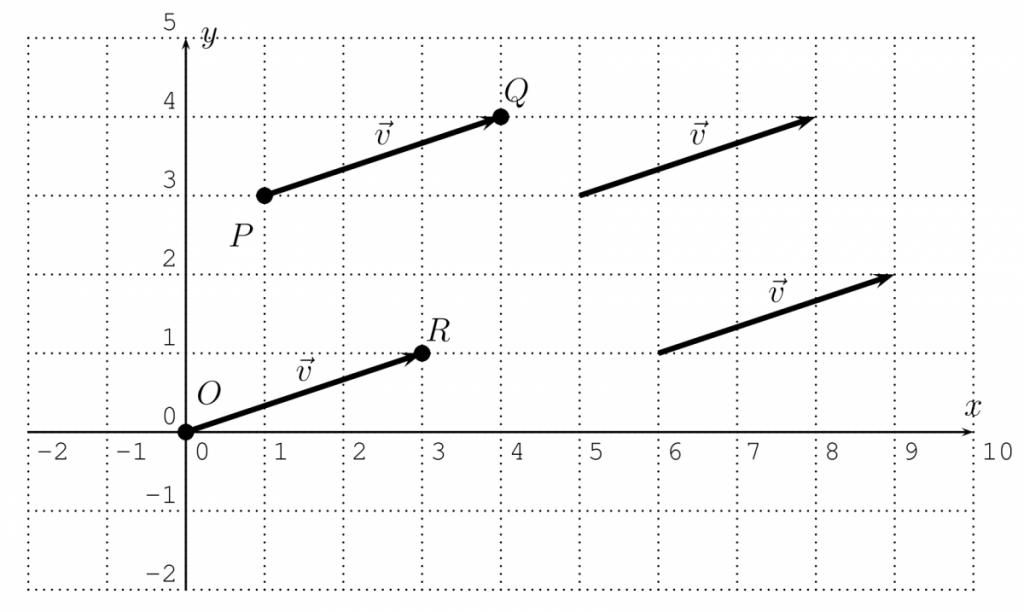
We can always represent a vector $\vec{v}$ by arranging the starting point of $\vec{v}$ to be the origin $O(0,0)$ (as in $\overrightarrow{O R}$ in the picture above). If $R$ has coordinates $R(a, b)$ then we also write for $\vec{v}=\overrightarrow{O R}$:
$\vec{v}=\langle a, b\rangle$, or $\vec{v}=\begin{bmatrix} a\\ b\end{bmatrix}$
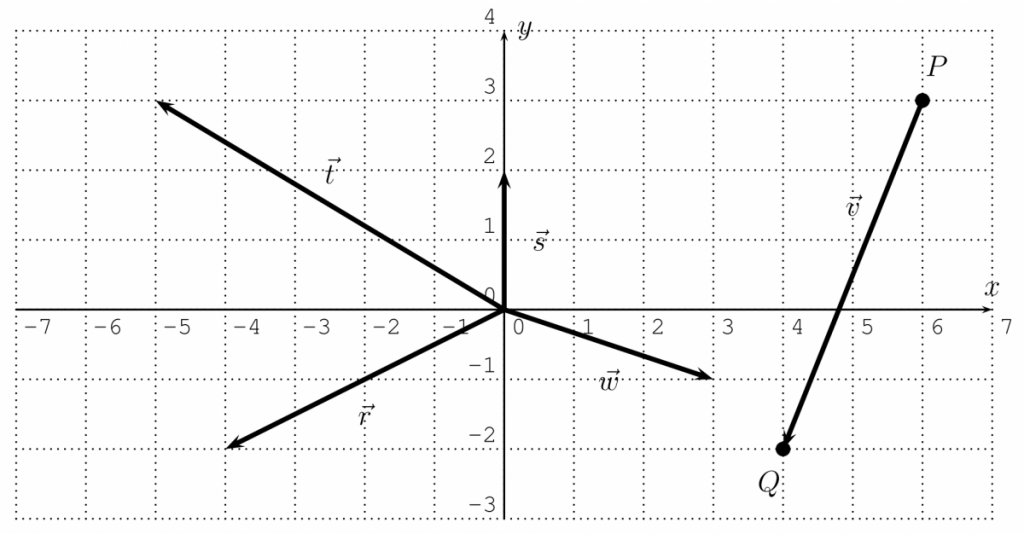
Example 22.2. Graph the vectors $\vec{v}, \vec{w}, \vec{r}, \vec{s}, \vec{t}$ in the plane, where
$\vec{v}=\overrightarrow{P Q}$ with $P(6,3)$ and $Q(4,-2),$ and
$\vec{w}=\langle 3,-1\rangle, \quad \vec{r}=\langle-4,-2\rangle, \quad \vec{s}=\langle 0,2\rangle, \quad \vec{t}=\langle-5,3\rangle$
The formulas for magnitude and directional angle of a vector are the same as those for modulus (magnitude) and argument (angle) of a complex number:
Formulas for magnitude and angle of a vector: Suppose $\vec{v}=\langle{a,b}\rangle}$ is a vector in the plane $\mathbb{R}^2$. Then the magnitude and angle of $\vec{v}$ are given by:
$||\vec{v}||=\sqrt{a^2+b^2}$, $\tan(\theta)=\frac{b}{a}$
Conversely, we can obtain the coordinates of a vector from its magnitude and directional angle by:
$\vec{v}=\langle||\vec{v}|| \cdot \cos (\theta),||\vec{v}|| \cdot \sin (\theta)\rangle$
Example 22.4. Find the magnitude and directional angle of the given vectors:
a) $\langle-6,6\rangle$
b) $\langle 4,-3\rangle$
c) $\langle-2 \sqrt{3},-2\rangle$
d) $\langle 8,4 \sqrt{5}\rangle$
e) $\overrightarrow{P Q}$, where $P(9,2)$ and $Q(3,10)$
VIDEO: Intro to vectors, finding magnitude and direction – Example 22.4
Operations on Vectors
There are two basic operations on vectors, scalar multiplication and vector addition.
Scalar Multiplication
Definition 22.5. The scalar multiplication of a real number $r$ with a vector $\vec{v}=\langle a, b\rangle$ is defined to be the vector given by multiplying each coordinate by $r$:
$r \langle a, b\rangle =\langle r \cdot a, r \cdot b\rangle$
Example 22.6. Multiply, and graph the vectors
a) $4 \cdot\langle-2,1\rangle$
b) $(-3)\cdot\langle-6,-2\rangle$
VIDEO: Scalar multiplication of vectors – Example 22.6
Observation. When we multiply a vector $\vec{v}$ by a positive real number $r>0$, the result will have the same angle as $\vec{v}$, while the magnitude will be stretched by a factor of $r$.
The Unit Vector
Definition 22.8. A vector $\vec{u}$ is called a unit vector if it has a magnitude of 1
$\vec{u}$ is a unit vector $\quad \Longleftrightarrow ||\vec{u}||=1$
There are two special unit vectors $\vec{i}$ and $\vec{j}$, which are the vectors pointing in the $x-$ and the $y$ -direction.
$\vec{i}=\langle 1,0\rangle \quad \text { and } \quad \vec{j}=\langle 0,1\rangle$
Example 22.9. Find a unit vector in the direction of $\vec{v}$
a) $\langle 8,6\rangle$
b) $\langle-2,3 \sqrt{7}\rangle$
VIDEO: Unit vectors – Example 22.9
Vector Addition
The second operation on vectors is called vector addition.
Definition 22.10. Let $\vec{v}=\langle a, b\rangle$ and $\vec{w}=\langle c, d\rangle$ be two vectors. Then the vector addition $\vec{v}+\vec{w}$ is defined by component-wise addition:
$\langle a, b\rangle+\langle c, d\rangle:=\langle a+c, b+d\rangle$
In the plane, this corresponds to starting at the origin, following $\vec{v}$ and then $\vec{w}$ (or vice versa, following $\vec{w}$ and then $\vec{v}$). In the picture, note that whichever path you take from the origin you will still arrive at the same point in the upper right, $\vec{v}+\vec{w}$:
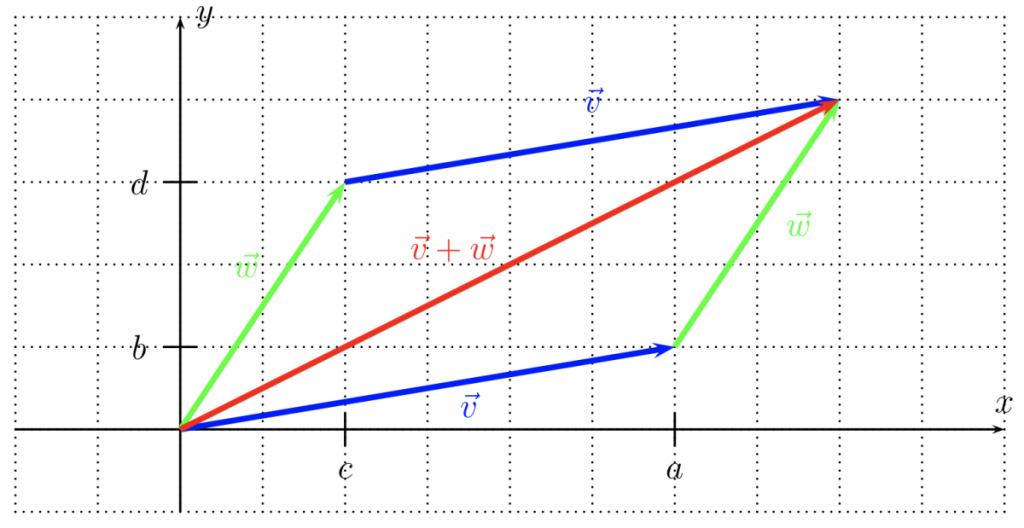
Example 22.11. Perform the vector addition and simplify as much as possible.
a) $\langle 3,-5\rangle+\langle 6,4\rangle$
b) $5 \cdot\langle-6,2\rangle-7 \cdot\langle 1,-3\rangle$
c) $4 \vec{i}+9 \vec{j}$
d) find $2 \vec{v}+3 \vec{w}$ for $\vec{v}=-6 \vec{i}-4 \vec{j}$ and $\vec{w}=10 \vec{i}-7 \vec{j}$
e) find $-3 \vec{v}+5 \vec{w}$ for $\vec{v}=\langle 8, \sqrt{3}\rangle$ and $\vec{w}=\langle 0,4 \sqrt{3}\rangle$
VIDEO: Vector addition – Example 22.11
Example 22.12. The forces $\vec{F}_{1}$ and $\vec{F}_{2}$ are applied to an object. Find the resulting total force $\vec{F}=\vec{F}_{1}+\vec{F}_{2}$. Determine the magnitude and directional angle of the total force $\vec{F}$. Approximate these values as necessary. Recall that the international system of units for force is the newton $\left[1 N=1 \frac{k g \cdot m}{s^{2}}\right]$
a) $\vec{F}_{1}$ has magnitude 3 newtons, and angle $\theta_{1}=45^{\circ}$
$\vec{F}_{2}$ has magnitude 5 newtons, and angle $\theta_{2}=135^{\circ}$
b) $\left|\vec{F}_{1}\right|=7$ newtons, and $\theta_{1}=\frac{\pi}{6},$ and $\left|\vec{F}_{2}\right|=4$ newtons, and $\theta_{2}=\frac{5 \pi}{3}$
VIDEO: Vector addition application (force) – Example 22.12
That’s it for now – give the WeBWorK a try!
Hi everyone! Read through the material below, watch the videos.
Lesson 21: Complex Numbers
Topic: This lesson covers Chapter 21: Complex numbers.
WeBWorK: There are four WeBWorK assignments on today’s material:
Complex Numbers – Operations
Complex Numbers – Magnitude
Complex Numbers – Direction
Complex Numbers – Polar Form
Question of the Day: What is the square root of $-1$?
Lesson Notes (Notability – pdf):
This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.
Review of Complex Numbers
How do we get the complex numbers? We start with the real numbers, and we throw in something that’s missing: the square root of $-1$.
Definition 21.1. We define the imaginary unit or complex unit to be:
$$i=\sqrt{-1}$$
The most important property of $i$ is: $\quad i^2=-1$
Definition 21.2. A complex number is a number of the form $a+bi$.
$a$ and $b$ are allowed to be any real numbers. $a$ is called the real part of $a+bi$, and $b$ is called the imaginary part of $a+bi$. The complex numbers are referred to as $\mathbb{C}$ (just as the real numbers are $\mathbb{R}$.
We can picture the complex number $a+bi$ as the point with coordinates $(a,b)$ in the complex plane.
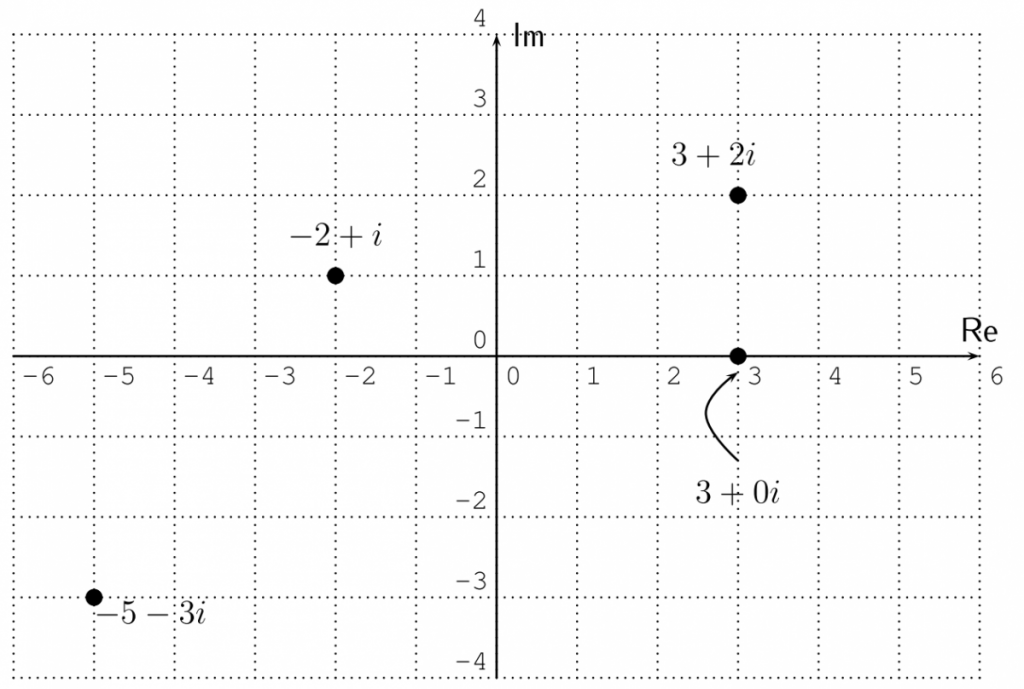
Example 21.3. Perform the operation.
a) $(2-3 i)+(-6+4 i)$
b) $(3+5 i) \cdot(-7+i)$
c) $\frac{5+4 i}{3+2 i}$
VIDEO: Review of Complex Numbers – Example 21.3
Polar form
Next, we will look at how we can describe a complex number slightly differently – instead of giving the $x$ and $y$ coordinates, we will give a distance $r$ (the modulus) and angle $\theta$ (the argument). We call this the polar form of a complex number.
Many amazing properties of complex numbers are revealed by looking at them in polar form! Let’s learn how to convert a complex number $a+bi$ into polar form, and back again.
Definition 21.4. Let $a+bi$ be a complex number. The absolute value of $a+bi$, denoted by $|a+bi|$, is the distance between the point $a+bi$ in the complex plane and the origin $(0,0)$. By the Pythagorean Theorem, we can calculate the absolute value of $a+bi$ as follows:
$$ |a+bi|=\sqrt{a^2+b^2}$$
Definition 21.6. Let $a+bi$ be a complex number. The coordinates in the plane can be expressed in terms of the absolute value, or modulus, $r=|a+bi|$ and the angle, or argument, $\theta$ formed with the positive real axis (the $x$-axis) as shown in the diagram:
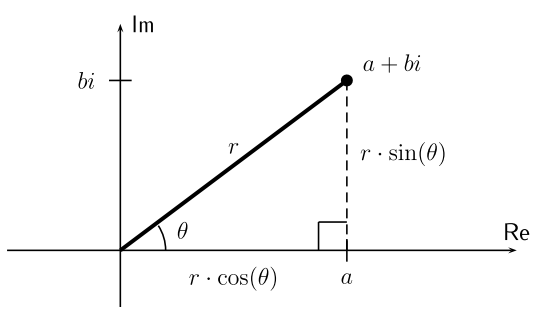
As shown in the diagram, the coordinates $a$ and $b$ are given by:
$a=r\cdot\cos(\theta), \text{ and } b=r\cdot\sin(\theta)$
Substituting and factoring out $r$, we can use these to express $a+bi$ in polar form:
Polar form: $a+bi = r\left(\cos(\theta) + i\cdot\sin(\theta)\right)$
How do we find the modulus $r$ and the argument $\theta$?
Note that $r$ is given by the absolute value. For $\theta$, we note that $\frac{b}{a}=\frac{r \cdot \sin (\theta)}{r \cdot \cos (\theta)}=\frac{\sin (\theta)}{\cos (\theta)}=\tan (\theta)$. This leads to the following:
Formulas for converting to polar form (finding the modulus $r$ and argument $\theta$): $r=\sqrt{a^2+b^2}$, $\tan(\theta)=\frac{b}{a}$
With regards to the modulus $\theta$, we can certainly use the inverse tangent function $\arctan\left(\frac{b}{a}\right)$. However, we have to be a little careful: since the arctangent only gives angles in Quadrants I and II, we need to doublecheck the quadrant of $(a,b)$.
If $\arctan\left(\frac{b}{a}\right)$ is in the correct quadrant then $\theta=\arctan\left(\frac{b}{a}\right)$. If not, then we add $\pi$ radians or $180^\circ$ to obtain the angle in the opposing quadrant: $\theta=\arctan\left(\frac{b}{a}\right)+\pi$, or $\theta=\arctan\left(\frac{b}{a}\right)+180^\circ$. You’ll see this in action in the following example.
Example 21.7. Convert the complex number to polar form.
a) $2+3 i$
b) $-2-2 \sqrt{3} i$
c) $4-3 i$
d) $-4 i$
VIDEO: Converting complex numbers to polar form – Example 21.7
Example 21.8. Convert the number from polar form into the standard form $a+bi$
a) $3 \cdot\left(\cos \left(117^{\circ}\right)+i \sin \left(117^{\circ}\right)\right)$
b) $4 \cdot\left(\cos \left(\frac{5 \pi}{4}\right)+i \sin \left(\frac{5 \pi}{4}\right)\right)$
VIDEO: Converting complex numbers from polar form into standard form – Example 21.8
Multiplication and division of complex numbers in polar form
Why is polar form useful? The primary reason is that it gives us a simple way to picture how multiplication and division work in the plane. The proposition below gives the formulas, which may look complicated – but the idea behind them is simple, and is captured in these two slogans:
When we multiply complex numbers: we multiply the $r$s and add the $\theta$s.
When we divide complex numbers: we divide the $r$s and subtract the $\theta$s
Proposition 21.9. Let $r_{1}\left(\cos \left(\theta_{1}\right)+i \sin \left(\theta_{1}\right)\right)$ and $r_{2}\left(\cos \left(\theta_{2}\right)+i \sin \left(\theta_{2}\right)\right)$ be two complex numbers in polar form. Then, the product and quotient of these are given by
$r_{1}\left(\cos \left(\theta_{1}\right)+i \sin \left(\theta_{1}\right)\right) \cdot r_{2}\left(\cos \left(\theta_{2}\right)+i \sin \left(\theta_{2}\right)\right) \ =r_{1} r_{2} \cdot\left(\cos \left(\theta_{1}+\theta_{2}\right)+i \sin \left(\theta_{1}+\theta_{2}\right)\right)$
$\frac{r_{1}\left(\cos \left(\theta_{1}\right)+i \sin \left(\theta_{1}\right)\right)}{r_{2}\left(\cos \left(\theta_{2}\right)+i \sin \left(\theta_{2}\right)\right)} =\frac{r_{1}}{r_{2}} \cdot\left(\cos \left(\theta_{1}-\theta_{2}\right)+i \sin \left(\theta_{1}-\theta_{2}\right)\right)$
Example 21.10. Multiply or divide the complex numbers, and write your answer in polar and standard form.
a) $5\left(\cos \left(11^{\circ}\right)+i \sin \left(11^{\circ}\right)\right) \cdot 8\left(\cos \left(34^{\circ}\right)+i \sin \left(34^{\circ}\right)\right)$
b) $\quad 3\left(\cos \left(\frac{5 \pi}{8}\right)+i \sin \left(\frac{5 \pi}{8}\right)\right) \cdot 12\left(\cos \left(\frac{7 \pi}{8}\right)+i \sin \left(\frac{7 \pi}{8}\right)\right)$
c) $\frac{32\left(\cos \left(\frac{\pi}{4}\right)+i \sin \left(\frac{\pi}{4}\right)\right)}{8\left(\cos \left(\frac{7 \pi}{12}\right)+i \sin \left(\frac{7 \pi}{12}\right)\right)}$
d) $\frac{4\left(\cos \left(203^{\circ}\right)+i \sin \left(203^{\circ}\right)\right)}{6\left(\cos \left(74^{\circ}\right)+i \sin \left(74^{\circ}\right)\right)}$
e) INTUITIVE BONUS: Without doing any calculation or conversion, describe where in the complex plane to find the number obtained by multiplying $(5+2i)(-1+6i)$.
VIDEO: Multiplication and division of complex numbers in polar form – Example 21.10
That’s it for today! Give the WeBWorK a try.
Hi everyone! Read through the material below, watch the videos, and send me your questions. Don’t forget to complete the Daily Quiz (below this post) before midnight to be marked present for the day.
Lesson 20: Trigonometric Equations
Lesson Date: Thursday, April 23rd.
Topic: This lesson covers Chapter 20: Trigonometric Equations.
WeBWorK: There is one WeBWorK assignment on today’s material, due next Thursday 4/30:
Trigonometry – Equations
Question of the Day: If we know $\sin(x)=\frac{1}{2}$, what do we know about the angle $x$?
Lesson NOtes (Notability – pdf):
This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.
Basic Trigonometric Equations
Equations of the form tan(x)=c
Example 20.1. Solve for $x$: $\tan(x)=\sqrt{3}$
VIDEO: Example 20.1, tan(x)=c
Observation 20.2. To solve $\tan(x)=c$, we first determine one solution $x=\tan^{-1}(c)$. Then the general solution is given by:
$$x=\tan^{-1}(c)+n\cdot\pi \text{ where }n = 0, \pm 1, \pm 2, \pm 3, …$$
EQUATIONS OF THE FORM cos(x)=c
Example 20.4. Solve for $x$: $\cos(x)=\frac{1}{2}$
VIDEO: Example 20.4, cos(x)=c
Observation 20.5. To solve $\cos(x)=c$, we first determine one solution $x=\cos^{-1}(c)$. Then the general solution is given by:
$$x=\pm\cos^{-1}(c)+2n\cdot\pi \text{ where }n = 0, \pm 1, \pm 2, \pm 3, …$$
EQUATIONS OF THE FORM sin(x)=c
Example 20.7. Solve for $x$: $\sin(x)=\frac{\sqrt{2}}{2}$
VIDEO: Example 20.7, sin(x)=c
Observation 20.8. To solve $\sin(x)=c$, we first determine one solution $x=\sin^{-1}(c)$. Then the general solution is given by:
$$x=(-1)^{n}\cdot\sin^{-1}(c)+n\cdot\pi \text{ where }n = 0, \pm 1, \pm 2, \pm 3, …$$
Summary: We summarize the different formulas used to solve the basic trigonometric equations in the following table.
| Solve: $\sin(x)=c$ | Solve: $\cos(x)=c$ | Solve: $\tan(x)=c$ |
| First, find one solution, that is: $\sin^{-1}(c)$. Use: $\sin^{-1}(-c)=-\sin^{-1}(c)$ | First, find one solution, that is: $\cos^{-1}(c)$. Use: $\cos^{-1}(-c)=\pi-\cos^{-1}(c)$ | First, find one solution, that is: $\tan^{-1}(c)$. Use: $\tan^{-1}(-c)=-\tan^{-1}(c)$ |
| The general solution is: $x=(-1)^{n} \sin^{-1}(c)+n \pi$ | The general solution is: $x=\pm \cos^{-1}(c)+2 n \pi$ | The general solution is: $x=\tan ^{-1}(c)+n \pi$ |
| where $n=0,\pm 1,\pm 2, \ldots$ | where $n=0,\pm 1,\pm 2, \ldots$ | where $n=0,\pm 1,\pm 2, \ldots$ |
Example 20.10. Find the general solution of the equation, and state at least $5$ distinct solutions.
a) $\sin(x)=-\frac{1}{2}$
b) $\cos(x)=-\frac{\sqrt{3}}{2}$
Equations involving trigonometric functions
Example 20.11. Solve for $x$
a) $2 \sin (x)-1=0$
b) $\sec (x)=-\sqrt{2}$
c) $7 \cot (x)+3=0$
VIDEO: Example 20.11 – equations with trig functions (linear)
Example 20.12. Solve for $x$.
a) $\tan ^{2}(x)+2 \tan (x)+1=0 \quad$ b) $2 \cos ^{2}(x)-1=0$
VIDEO: Example 20.12 – equations with trig functions (quadratic)
Hi everyone! Read through the material below, watch the videos.
Lesson 19: Inverse trigonometric functions
Topic: This lesson covers Chapter 19: Inverse trigonometric functions.
WeBWorK: There is one WeBWorK assignment on today’s material:
Trigonometry – Inverse Functions
Question of the Day: Are the trigonometric functions $\sin(x),\cos(x)$ and $\tan(x)$ one-to-one functions?
Lesson Notes (Notability – pdf):
This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.
The functions $\sin^{-1}, \cos^{-1},\tan^{-1}$
In this section, we are interested in the inverse functions of the trigonometric functions $y=\sin(x), y=\cos(x),$ and $y=\tan(x)$. You may recall from our work earlier in the semester that in order for a function to have an inverse, it must be one-to-one (or pass the horizontal line test: any horizontal line intersects the graph at most once).
The function $\tan^{-1}(x)$
Recall the graph of the function $y=\tan(x)$:
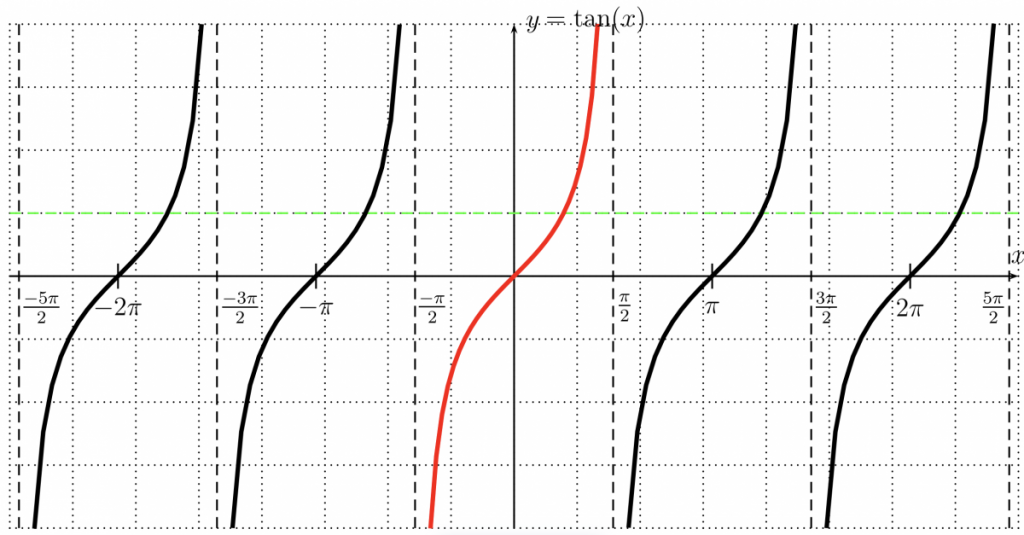
Notice that since the graph consists of a repeating pattern of vertical stripes, any horizontal line will touch the graph in multiple places – this graph FAILS the horizontal line test (it is NOT one-to-one). How can we define the inverse? By restricting the domain – that is, only looking at one of the repeating vertical stripes. If we only look at the part of the graph between $-\frac{\pi}{2}$ and $\frac{\pi}{2}$ then the function is one-to-one (that it, the red part of the function above is, by itself, one-to-one).
Definition 19.1. The inverse of the function $y=\tan (x)$ with restricted domain $D=\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)$ and range $R=\mathbb{R}$ is called the inverse tangent or arctangent function. It is denoted by:
$y=\tan ^{-1}(x) \quad$ or $\quad y=\arctan (x) \quad \Longleftrightarrow \quad \tan (y)=x, \quad y \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$
Note that the inverse tangent function is written both $\tan^{-1}(x)$ and $\arctan(x)$ — they mean the same thing.
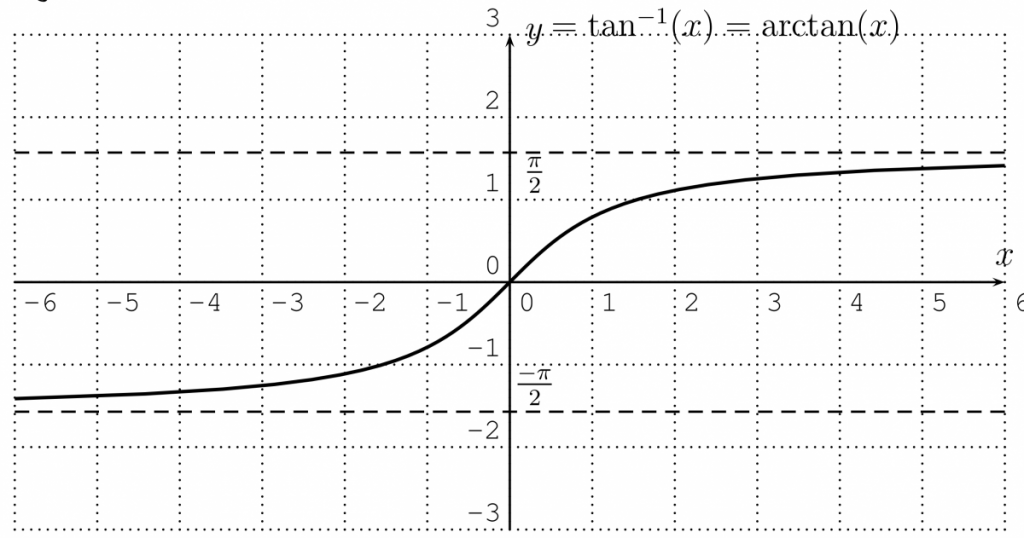
Observation: The inverse tangent is an odd function, so $\tan^{-1}(-x)=-\tan^{-1}(x)$
(recall that a function $f(x)$ is odd provided $f(-x)=-f(x)$)
Example 19.1 Recall the exact values of the tangent function from Chapter 17:
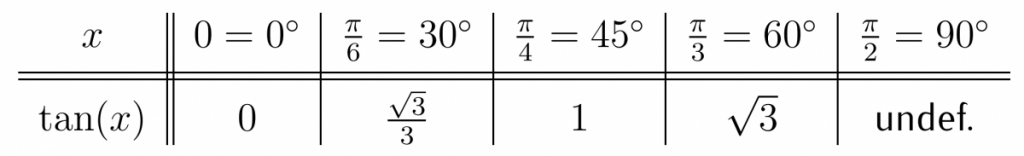
Use the table and Observation above to find exact values of the inverse tangent function. Give answers in both degrees and radians.
a. $\arctan(1)$ b. $\arctan\left(-\frac{\sqrt{3}}{3}\right)$. c. $\tan^{-1}(0)$
VIDEO: The Inverse Tangent Function – Definition and Example 19.1
THE FUNCTION $\sin^{-1}(x)$
Consider the graph of the function $y=\sin(x)$. It is not one-to-one either:
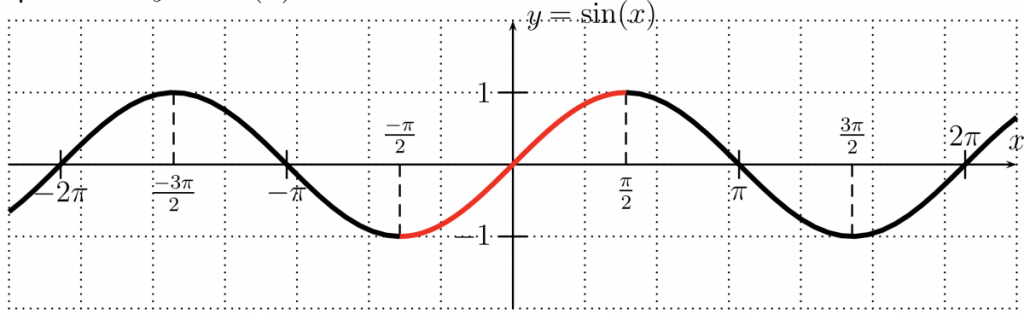
However, if we restrict the function to the interval $\left[-\frac{\pi}{2},\frac{\pi}{2}\right]$ (shown in red) the resulting function is one-to-one, and so we can consider the inverse function.
Definition 19.5. The inverse of the function $y=\sin (x)$ with restricted domain $D=\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]$ and range $R=[-1,1]$ is called the inverse sine or arcsine function. It is denoted by
$y=\sin ^{-1}(x) \quad \text { or } \quad y=\arcsin (x) \quad \Longleftrightarrow \quad \sin (y)=x, \quad y \in\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]$
The arcsine reverses the input and output of the sine function, so that the arcsine has domain $D=[-1,1]$ and range $R=\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]$.
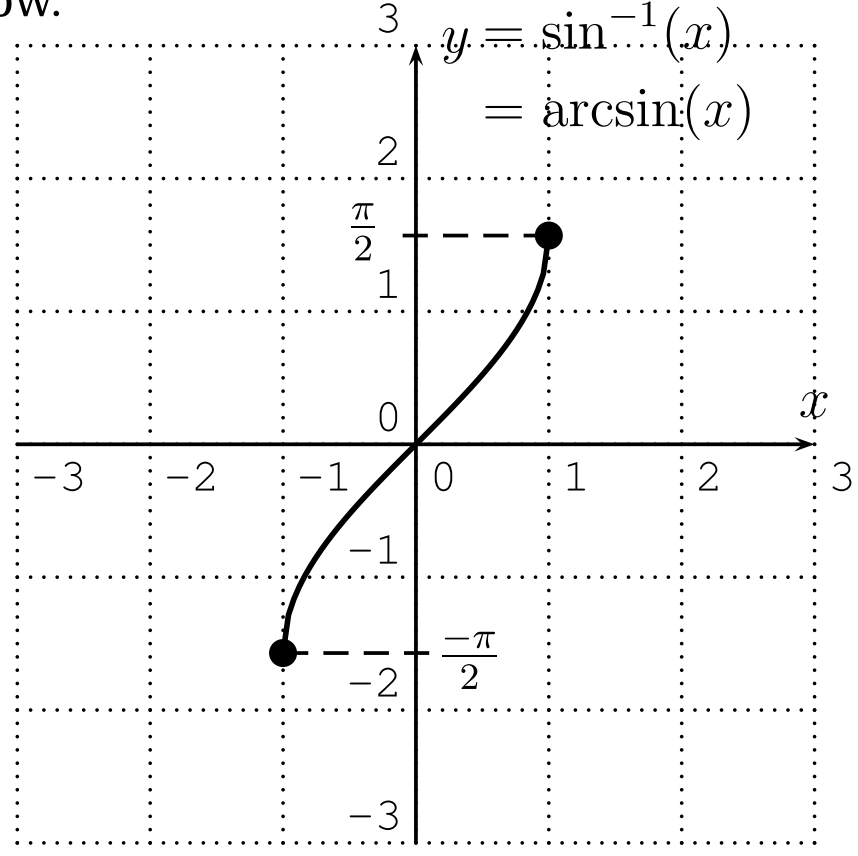
Observation: The inverse sine function is an odd function, so $\sin^{-1}(-x)=-\sin^{-1}(x)$.
Example 19.7. Recall the values of the sine function for common angles:
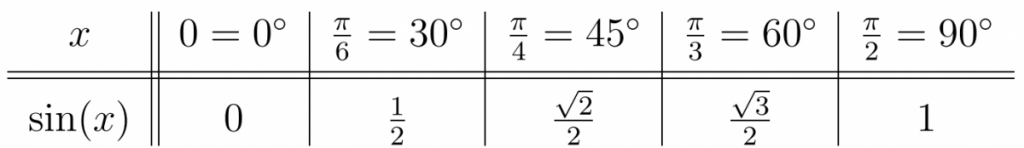
Use the Table and Observation above to find exact values of the arcsine function. Give answers in both degrees and radians.
a. $\sin ^{-1}\left(\frac{\sqrt{2}}{2}\right)$, b. $\sin^{-1}(1)$, c. $\sin^{-1}(0)$, d. $\sin ^{-1}\left(\frac{-1}{2}\right)$, e. $\sin^{-1}(3)$
VIDEO: The Inverse Sine Function – Definition and Example 19.7
THE FUNCTION $\cos^{-1}(x)$
We treat the function $\cos(x)$ similar to $\sin(x)$. However, we are no longer able to use the interval $\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]$. Why?

In order to make the cosine function one-to-one, we restrict to the interval $[0,\pi]$.
Definition 19.8. The inverse of the function $y=\cos (x)$ with restricted domain $D=[0, \pi]$ and range $R=[-1,1]$ is called the inverse cosine or arccosine function. It is denoted by
$y=\cos ^{-1}(x) \quad \text { or } \quad y=\arccos (x) \quad \Longleftrightarrow \quad \cos (y)=x, \quad y \in[0, \pi]$
The arccosine reverses the input and output of the cosine function, so that the arccosine has domain $D=[-1,1]$ and range $R=[0, \pi]$.
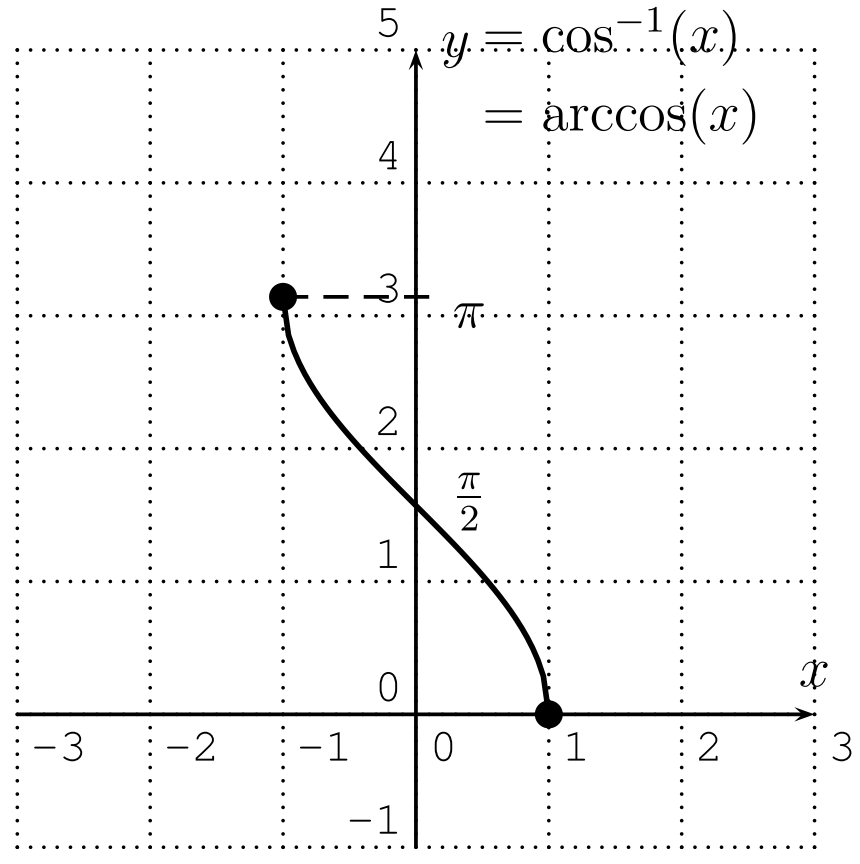
Observation: The arccosine function is neither even nor odd. However, it does obey the following symmetry: $\cos^{-1}(-x)=\pi-\cos^{-1}(x)$
(in many problems, you can avoid the use of this formula by remembering the unit circle definition of cosine).
Example 19.10. Recall the values of the cosine function for common angles:
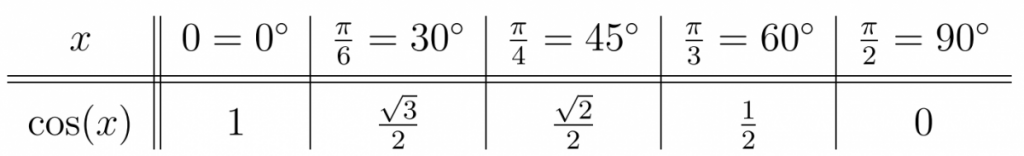
Use the Table and Observation above to find exact values of the arccosine function. Give answers in both degrees and radians.
a. $\arccos\left(\frac{\sqrt{3}}{2}\right)$, b. $\cos^{-1}(1)$, c. $\cos ^{-1}(0)$, d. $\arccos=\left(-\frac{1}{2}\right)$, e. $\arccos(2)$
VIDEO: The Inverse Cosine Function – Definition and Example 19.10
Inverse trig functions on the TI-84+ calculator
How do we find values of inverse trig functions that don’t appear in our “common angles” table?
Example. Find the values of the inverse trig functions using a calculator. Include at least 5 decimal digits past the decimal point.
a. $\arccos(0.35)$ (in radians)
b. $\tan^{-1}(-13.2)$ (in degrees)
VIDEO: Inverse trig functions on the calculator
RECALL: Converting between radians and degrees
$\text{radians}=\text{degrees}\cdot\frac{\pi}{180}$
$\text{degrees}=\text{radians}\cdot\frac{180}{\pi}$
Hi everyone! Read through the material below, watch the videos, collect your questions.
Lesson 18: Addition of angles and multiple angle formulas
Topic: This lesson covers Chapter 18: Addition of angles and multiple angle formulas.
WeBWorK: There are two WeBWorK assignments on today’s material:
Trigonometry – Sum and Difference Formulas
Trigonometry – Double and Half Angle Formulas
Lesson Notes (Notability – pdf):
This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.
Question of the Day: Suppose we know the values of the trig functions of two angles $a$ and $b$. Can we use them to find the values of the trig functions of the angle $a+b$?
Today, we will see how we can do exactly that – the idea is to work with formulas that allow us to calculate, for example, $\sin(a+b)$ and $\cos(a+b)$ based on the values of $\sin(a),\cos(a),\sin(b),$ and $\cos(b)$.
NOTE: We often use greek letters for angles — this helps us keep track of what’s an angle and what’s not. The most common are the greek letters alpha $\alpha$ and beta $\beta$. We’ll be using these instead of $a$ and $b$.
Warning: the videos for today’s lecture are *quite long* – however, they consist almost entirely of examples, with a lot of explanation. Feel free to skip around, or to try the WeBWorK first (if you get stuck, the videos might help).
Addition and Subtraction of Angles
Proposition 18.1. For any angles $\alpha$ and $\beta$,
- $\sin (\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta$
- $\sin (\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta$
- $\cos (\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha \sin \beta$
- $\cos (\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta$
- $\tan (\alpha+\beta)=\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}$
- $\tan (\alpha-\beta)=\frac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}$
Where did these formulas come from!?
Great question! To answer it, you need to see the *proof* of these formulas – this appears in your book in Chapter 18.
Now, we are going to see how these formulas let us calculate the values of trig functions at many different angles, based on just a few common angles (such as those listed in the table below – if you don’t know them, this is a great time to learn them!).
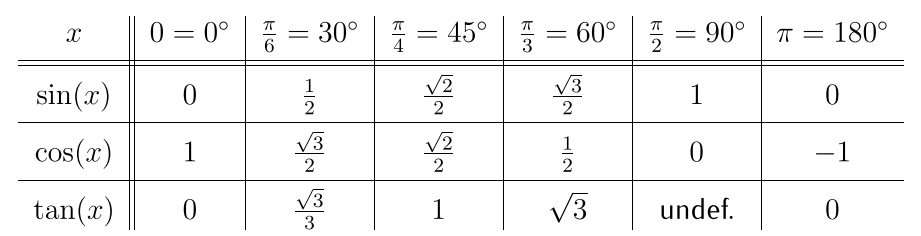
Example 18.2. Find the exact values of the trigonometric functions:
a) $\cos \left(\frac{\pi}{12}\right)$
b) $\tan \left(\frac{5 \pi}{12}\right)$
c) $\cos \left(\frac{11 \pi}{12}\right)$
VIDEO: Example 18.2 applying angle sum and difference formulas
Double and Half Angles
Proposition 18.5. Let $\alpha$ be any angle. Then we have the half-angle formulas:
$\sin \frac{\alpha}{2} =\pm \sqrt{\frac{1-\cos \alpha}{2}}$
$\cos \frac{\alpha}{2} =\pm \sqrt{\frac{1+\cos \alpha}{2}}$
$\tan \frac{\alpha}{2} =\frac{1-\cos \alpha}{\sin \alpha}=\frac{\sin \alpha}{1+\cos \alpha}=\pm \sqrt{\frac{1-\cos \alpha}{1+\cos \alpha}}$
and the double-angle formulas:
$\sin (2 \alpha) =2 \sin \alpha \cos \alpha$
$\cos (2 \alpha) =\cos ^{2} \alpha-\sin ^{2} \alpha=1-2 \sin ^{2} \alpha=2 \cos ^{2} \alpha-1$
$\tan (2 \alpha) &=\frac{2 \tan \alpha}{1-\tan ^{2} \alpha}$
Example 18.6. Find the exact values of the trigonometric functions:
a) $\sin \left(\frac{\pi}{8}\right)$
b) $\cos \left(\frac{9 \pi}{8}\right)$
c) $\tan \left(\frac{\pi}{24}\right)$
VIDEO: Example 18.6 applying half-angle formulas
Example 18.7. Find the trigonometric functions of $2\alpha$ when $\alpha$ has the properties below.
a) $\sin (\alpha)=\frac{3}{5},$ and $\alpha$ is in quadrant 1
b) $\tan (\alpha)=\frac{12}{5},$ and $\alpha$ is in quadrant 2
VIDEO: Example 18.7 applying double-angle formulas
That’s it for now. Take a look at the WeBWorK!
Hi everyone! Read through the material below, watch the videos, and collect your questions.
Lesson 17: Trigonometric functions
Topic: This lesson covers Chapter 17: Trigonometric functions.
WeBWorK: There are five WeBWorK assignments on today’s material:
Trigonometry - Unit Circle,Trigonometry - Graphing Amplitude,Trigonometry - Graphing Period,Trigonometry - Graphing Phase Shift, andTrigonometry - Graphing Comprehensive
Today we start trigonometric functions. We’ll begin with a review of the basics of trigonometry — if you remember everything about trigonometry, you can skip this part (but please don’t!). Then we’ll think about how these behave as functions, and look at their graphs.
Lesson Notes (Notability – pdf):
This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.
Review of trigonometry
a. Angles
We measure angles using two different systems, degrees and radians. In degrees, a full circle is $360^\circ$. In radians, a full circle is $2\pi \text{rad}$. Thus, we have $360^\circ=2\pi$ radians. If we consider a half-circle (divide both sides by two), we get:
$$180^\circ=\pi$$
Although most people are more familiar with degrees from their day-to-day lives, most mathematics at this level and above use radians. It will help you to get familiar with common angles in radians! The first video gives a review.
Why do mathematicians and scientists prefer radians to degrees? Great question!
VIDEO: Review of angles, radian measure
b. Trigonometric Functions
Definition. To define the trigonometric functions, we consider the following diagram: the initial side of an angle $x$ lies on the positive x-axis, and the terminal side of the angle passes through a point $P(a,b)$.
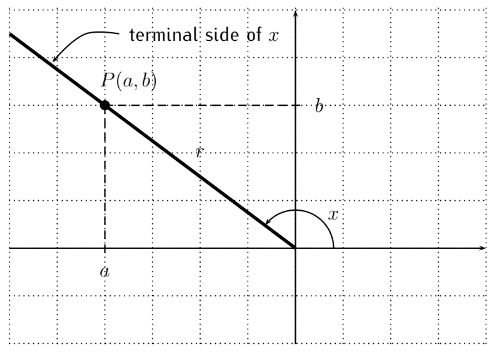
The distance from the origin $(0,0)$ to the point $P$ is $r$ (note: if we know $a$ and $bg$ we can calculate $r$ by using the Pythagorean Theorem, $r=\sqrt{a^2+b^2}$). Then the trigonometric functions (sine, cosine, tangent, cosecant, secant, cotangent) of $x$ are defined:
$$\sin(x)=\frac{b}{r},\quad \cos(x)=\frac{a}{r},\quad\tan(x)=\frac{a}{b}$$
$$\csc(x)=\frac{r}{b},\quad \sec(x)=\frac{r}{a},\quad\cot(x)=\frac{b}{a}$$
VIDEO: Review – definitions of trigonometric functions
Next, we need to know the values of the trig functions for some common angles. Once again, this is a review of material from previous courses – the following video will take you through some examples, but for more details I recommend checking out the videos on our video resource page.
VIDEO: Values of trig functions at common angles
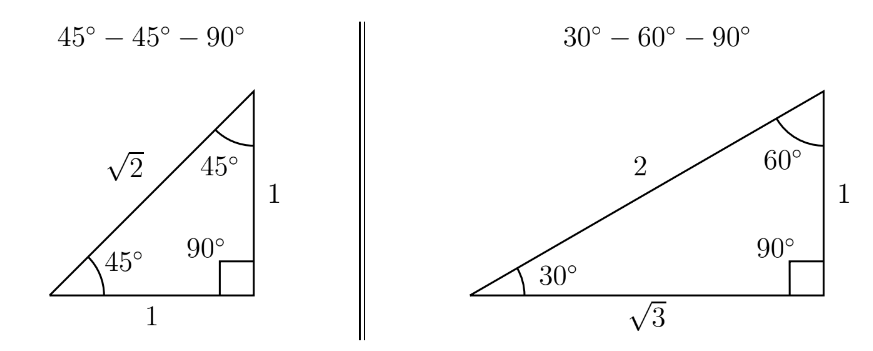
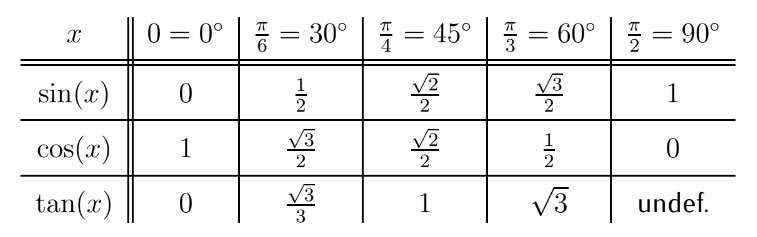
This is the end of the ‘review’ part of the lesson. Need a little more help? Take a look at the videos on our video resource page.
Graphs of trigonometric functions
Now we turn to the main idea of this lesson. We begin by looking at the graphs of the basic trig functions, $\sin x$, $\cos x$, and $\tan x$.
VIDEO: Graphs of basic trig functions
Example 17.8. Graph the following functions:
$f(x)=\sin (x)+3,\quad g(x)=4 \cdot \sin (x), \quad h(x)=\sin (x+2),\quad i(x)=\sin (3 x)$
$j(x)=2 \cdot \cos (x)+3, \quad k(x)=\cos (2 x-\pi), \quad l(x)=\tan (x+2)+3$
VIDEO: Example 17.8 modifying the graphs of trig functions – amplitude, period, phase shift.
Definition 17.9. Let $f$ be one of the functions:
$f(x)=a \cdot \sin (b \cdot x+c) \quad \text { or } \quad f(x)=a \cdot \cos (b \cdot x+c)$
The number $|a|$ is called the amplitude, the number $\left|\frac{2 \pi}{b}\right|$ is the period, and the number $\frac{-c}{b}$ is called the phase shift.
That’s it for now. Take a look at the WeBWorK!
Hi everyone! Read through the material below, watch the videos, collect your questions.
Lesson 15-16: Applications of Exponential and Logarithmic Functions
Topic: This lesson covers Chapter 15: Applications of Exponential and Logarithmic Functions and Chapter 16: Half-Life and Compound Interest.
WeBWorK: There is one WeBWorK assignment on today’s material:
Exponential Functions - Growth and Decay.
We study exponential functions because they are amazingly good at describing real-world phenomena. Today we will look at several different applications of exponential functions, including population growth and virus spread.
Lesson Notes (Notability – pdf):
This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.
Exponential growth and decay
RECALL: If $f(x)$ is an exponential function, then $f(x)=c\cdot b^x$.
NOTE: You can determine the values of $c$ and $b$ from any two points (input-output) on the graph.
Example 15.1.
a) $f(0)=4, \quad f(1)=20$
c) $f(2)=160, \quad f(7)=5$
Example 15.3 The population size of a country was $12.7$ million in the year 2000, and $14.3$ million in the year 2010.
a) Assuming an exponential growth for the population size, find the formula for the population depending on the year $t$ (where $t=0$ in the year 2000.
b) What will the population size be in the year 2015, assuming the formula holds until then?
c) When will the population reach 18 million?
You will often see exponential growth and decay functions written in a slightly different (but equivalent) form, using the number $e = 2.718…$ as a base. It’s also traditional to use $t$ (for time) instead of $x$ as our independent variable.
FACT. If $f(t)$ is an exponential function, then $f$ can be written as $f(t)=Pe^{rt}$. In this form:
- $t$ represents time
- $P$ is the initial amount
- $r$ is the growth rate (if $r$ is positive, we have exponential growth, if $r$ is negative we have exponential decay)
- $f(t)$ is the amount remaining at time t
- $e=2.718…$
QUESTION: What’s the connection between $f(x)=c\cdot b^x$ and $f(t)=Pe^{rt}$?
Definition (exponential decay). The half-life of a substance is the time it takes for the amount to be cut in half.
EXAMPLE: A study published on March 17th, in the New England Journal of Medicine found experimentally that the half-life of the Covid-19 virus in the air is approximately 1.15 hours. A single cough by an infected person can release up to 6 billion coronavirus molecules into the air. Let’s consider what happens after a single cough by an infected person.
- a. Model the number of remaining virus molecules $V(t)$ in the air at time $t$ by an exponential function $V(t)=Pe^{rt}$ (find $P,r$).
- b. How many of virus molecules will remain viable 5 hours after the person coughed?
- c. How long will it take for the number of remaining molecules to reach $6$ million ($0.1\%$ of the original amount)?
That’s it for now. Take a look at the WeBWorK!


