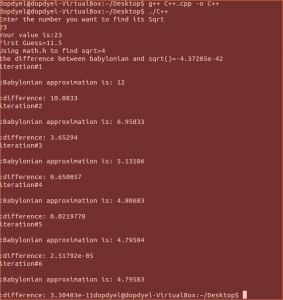
Lab Description:
The Lab 5 was about using Babylonian Algorithm method to get the approximate square root of an input by using a while, for loops to repeat the equation over and over again. the purpose was to get as close to the actual square root as possible. The Babylonian Equation that I used is xn+1=(xn+x/xn)/2. I translated this equation to understand better into guess2=(guess2 + (x/guess2))/2. Overall this lab was easy except if you don’t understand the equation than it will be difficult. Also, I would like to add that #include<iostream> and #include<math.h> are missing because of technical problem from openlab.
#include
#include
using namespace std;
int main(){
double d;
double x;
double xn=2;
double guess1;
double guess2=1;
double diff;
int y;
cout<<"Enter the number you want to find its Sqrt \n"; cin>>x;
cout<<"Your value is:"<<x<<endl;
guess1=x/2;
cout<<"First Guess="<<guess1<<endl;
y=sqrt(x);
cout<<"Using math.h to find sqrt="<<y<<endl;
cout<<"the difference between babylonian and sqrt()="<<diff;
for(d=0; d<6; d++)
{
cout<<"\niteration#"<<d+1<<endl;
guess2=(guess2 + (x/guess2))/2;
cout<<"\n:Babylonian approximation is: "<<guess2<<endl;
diff=guess2-(x/guess2);
cout<<"\n:difference: "<<diff;
}
diff=guess2-y;
return 0;
}
Screenshot