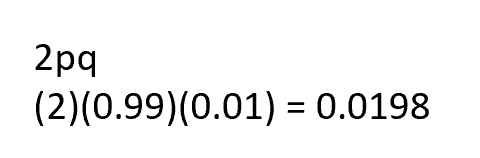Hardy-Weinberg Principle

The Hardy-Weinberg principle is a mathematical model used to describe the equilibrium of two alleles in a population in the absence of evolutionary forces. This model was derived independently by G.H. Hardy and Wilhelm Weinberg. It states that the allele and genotype frequencies across a population will remain constant across generations in the absence of evolutionary forces. This equilibrium makes several assumptions in order to be true:

  1. An infinitely large population size
  2. The organism involved is diploid
  3. The organism only reproduces sexually
  4. There are no overlapping generations
  5. Mating is random
  6. Allele frequencies equal in both genders
  7. Absence of migration, mutation or selection

As we can see, many items in the list above can not be controlled for but it allows for us to make a comparison in situations where expected evolutionary forces come into play (selection etc.).

Hardy-Weinberg Equilibrium

The alleles in the equation are defined as the following:

  • Genotype frequency is calculated by the following:\text{\Large genotype frequency} = \frac{\text{\Large \# individuals of given genotype}}{\text{\Large total \# individuals in population}}
  • Allele frequency is calculated by the following:\text{\Large allele frequency} = \frac{\text{\Large \# of copies of an allele in a population}}{\text{\Large total \# of alleles in population}}
  • In a two allele system with dominant/recessive, we designate the frequency of one as p and the other as q and standardize to:
    • \textit{\Large p} =\text{\Large Dominant allele frequency}
    • \textit{\Large q} =\text{\Large recessive allele frequency}
  • Therefore the total frequency of all alleles in this system equal 100% (or 1)
    • {\Large p + q = 1}
  • Likewise, the total frequency of all genotypes is expressed by the following quadratic where it also equals 1:
    • {\Large p^2 + 2pq + q^2 = 1}
    • This equation is the Hardy-Weinberg theorem that states that there are no evolutionary forces at play that are altering the gene frequencies.

Practice Hardy-Weinberg Problems

Question 1

The frequency of two alleles in a gene pool is 0.19 (A) and 0.81(a). Assume that the population is in Hardy-Weinberg equilibrium.

(a) Calculate the percentage of heterozygous individuals in the population.

Solution: In the equation p2 + 2pq + q2 = 1, the 2pq represents the heterozygotes. The question already gives us p (0.19) and q (0.81).

The percentage of heterozygous individuals is 31%.

(b) Calculate the percentage of homozygous recessive individuals in the same population.

Solution: In the equation p2 + 2pq + q2 = 1, the q2 represents the recessive individuals. The question already gives us the value of q (0.81).

The percentage of recessive individuals is 66%.

Question 2

An allele W, for white wool, is dominant over allele w, for black wool. In a sample of 900 sheep, 891 are white and 9 are black. Calculate the allelic frequencies within this population, assuming that the population is in Hardy-Weinberg equilibrium.

Solution: It is best to start with the 9 black sheep because they are recessive. We know these black sheep have a genotype of ww. We are less certain of the white sheep, which could be either WW or Ww.

We need to find out what percentage of the sheep population is black (ww). This will give us the value for q2.

So q2 is equal to 0.01. The question asked for the frequency of the allele, which is q. To find q, take the square root of q2.

The frequency of the recessive allele w is 0.1. We can now use this to find the frequency of the dominant allele W. According to Hardy-Weinberg, p + q = 1. We already have the value of q.

The frequency of the recessive allele is 0.1 and the frequency of the dominant allele is 0.9.

Question 3

In the United States, approximately one child in 10,000 is born with PKU (phenylketonuria), a syndrome that affects individuals homozygous for the recessive allele (aa).

(a) Calculate the frequency of the recessive allele in the population.

Solution: The main question gives us the frequency of the recessive genotype (aa): 1 in 10,000. We can use this to find the frequency of the recessive allele (a).

The frequency of the recessive allele is 0.01.

(b) Calculate the frequency of the dominant allele.

Solution: We know that p + q =1. We already found q above.

The frequency of the dominant allele is 0.99.

(c) Calculate the percentage of carriers of the trait within the population.

Solution: The carriers are individuals who are heterozygous (Aa). In the equation p2 + 2pq + q2 = 1, the 2pq represents the heterozygotes. We already found the values of p and q.

The percentage of the population that are carriers is 1.98% or 2%.

Return to Lab Main Page