Plane geometry
Our geometric intuition is grounded in our experience of the real world. For many basic concepts in geometry, that intuition is a great (indeed, fantastic) tool! However, it can be helpful to recognize some of the underlying assumptions we make about geometry and geometric objects that come from our real-world experience.
Many basic concepts will not be defined here — for example, point, line, plane, angle, and so on (you can take a look at Wu RLE Chapters 4 and 5 for a detailed exposition of basic concepts). It’s also important to note at the outset that the geometry curriculum does NOT make use of a coordinate plane (complete with x- and y- axes, etc), but just a “plain plane” – so things like coordinates of points, and the use of equations to describe lines and other figures, will not appear.
The point of this form of geometry is that it can be done independently of calculations and numbers. I think this is an important idea to teach: mathematics is not about numbers, but about objects adhering to certain rules (axioms).
Math.SE user Greg Graviton
When a coordinate plane is introduced, the subject becomes analytic geometry (and is concerned with equations of lines, circles, and so on).
What does it mean for two objects to be “the same”?
Example. Consider two pieces of paper. Are they the same? If I give them to two different students, do the students have the same piece of paper? What is the same about them? How can we tell? (lay one on top of the other).
Example. What does it mean for two points to be “the same”?
Example: What does it mean for two line segments to be “the same”?
In particular, what’s the idea in the plane that corresponds to our real-world notion of “moving one thing on top of the other”? We don’t literally move things like triangles and line segments around! How do we describe what’s going on mathematically?
The basic notion that will describe so much of our work in the plane is called a transformation – a function from the plane to itself.
Transformation
Let $\Pi$ denote the plane. A transformation $F$ of $\Pi$ is a rule that assigns to each point $P$ of $\Pi$ a unique point $F(P)$ (read: “$F$ of $P$” ) in $\Pi$.
We also say $F$ maps $P$ to $F(P)$ or, sometimes, $F$ moves $P$ to $F(P)$. Indeed, it is intuitively appealing to think of a transformation as a way of “moving” the points of the plane around.
Discuss the language: instead of “moving a point from one place to another,” we talk about the “image of a point under a transformation.”
Definition. We call two subsets of the plane congruent if there is an isometry taking one to the other.
Isometry
A transformation $F$ is an isometry if it preserves distances/lengths (sometimes called a rigid motion). That is, if $\operatorname{dist}(P,Q) = \operatorname{dist}(F(P),F(Q))$ for all $P, Q$ in $\Pi$.
NOTE: Preserving distance is a very strong property – in fact, any isometry also preserves angles, maps lines to lines and circles to circles, and so on.
The basic isometries
Rotation around a point $P$ by angle $t$ ($t$ is measured in degrees, if $t$ is positive then the rotation is counterclockwise, if $t$ is negative the rotation is clockwise).
Reflection across a line $L$.
Translation along a vector $\overrightarrow{AB}$.
Note that we can do multiple transformations in a row, and the result is a new transformation – this exactly corresponds to composition of functions.
Question: If we do multiple isometries in a row, is the result an isometry?
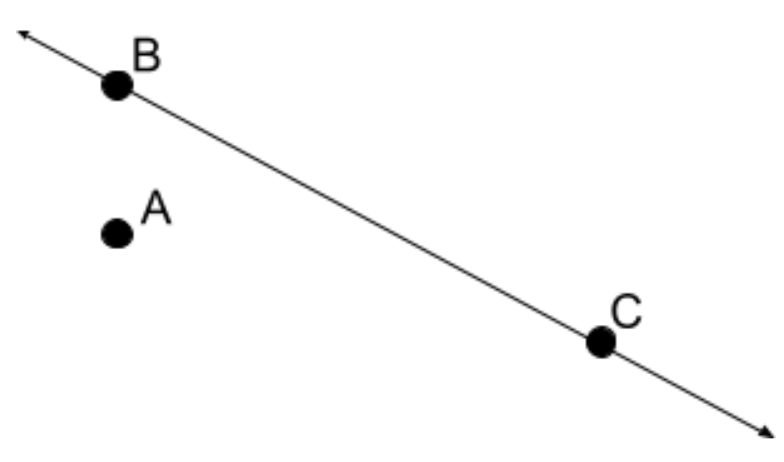
Example
Suppose $F$ is the rotation of $90^\circ$ about the point $A$, and $G$ is the reflection across the line $\overline{BC}$.
- Locate $F(B), F(C), F(A)$ (referred to as the image of B, C, and A under the transformation $F$).
- Locate $G(A), G(B), G(C)$.
Now suppose we *first* do $F$, followed by $G$.
- Locate $G(F(B)), G(F(C)), G(F(A))$.
- Locate $F(G(B)), F(B(C)), F(G(A))$.
Congruent
A subset $S$ of the plane is congruent to another subset $S^\prime$ of the plane if there is an isometry $F$ so that $F(S)=S^\prime$. In symbols, we say $S\cong S^\prime$.



Leave a Reply