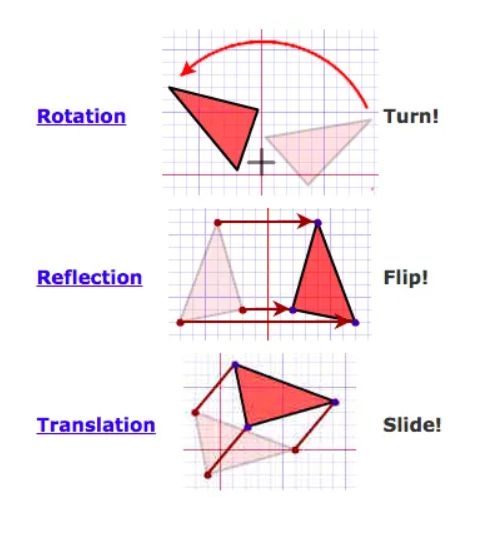
When we think about objects in the real world we definitely put something like a sheet of paper on top of another. In the world of geometry that is not always the case especially if you can’t rely the x and y plane. So how exactly would we determine if say a triangle or some other shape is the same without coordinates? Well if you remember how transformations of graphs work in algebra it’s pretty much the same concept. You would use a transformation to “move” the shape from one place to another. Now this is easier to see via the x and y plane but the idea is the same without it as well. There are three ways to “move” object and still end up with a shape that is mathematically the same or as we say congruent. The first way is a rotation which as the name suggests turns a shape left or right a certain number of degrees. The second way is a reflection this is where we flip something as if the shape is being showed by a mirror. The mirror image is the transformed version of the shape we started with. The last technique is called a translation where you slide a shape by whatever is added to what is given. Think y=x^2 and y=x^2-3 if you need a visual example of the same concept but a different application here. With all of these transformations we see that the lengths or distances if you are on the x and y plane are the same these movements are called rigid motions. If for example you have something where you have two shapes that look exactly the same but are a different size they are equal but we can say that they are similar to each other.



Leave a Reply