by: Sherly Gonzalez
A linear combination of two numbers is for instance: given “a” and “b” it would be na + mb, where m and n would be integers. For example some linear combinations of 8 and 12 are: let a = 8 and b = 12 so we can have 8(1) + 12(0) = 8; 8(0) + 12(1) = 12; 8(1) + 12(1) = 20; 8(-1) + 12(1) = 4; etc. You slowly get the gist of it, Now very briefly, a Greatest Common Divisor is the largest number possible to go into another number evenly, we can call the divisor “a” for the equation b= n * a for some integer n. For instance, the greatest common divisor also known as the greatest common factor for 16 and 24 is 8, although 16 and 24 are divisible by 1, 2 and itself the largest number was 8 . Therefore, the connection between linear combinations and the greatest common divisor is a theorem stating, if “a” and “b” are integers then the smallest positive number that is a linear combination of “a” and “b” is exactly equal to the greatest common divisor of (a,b). For example: what is the smallest positive integer to make a linear combination of 10 and 25. In that case we start with 10(-2) + 25(1) and get 5 as our answer. You can then also solve systems of equations using linear combinations when trying to solve for the variables.
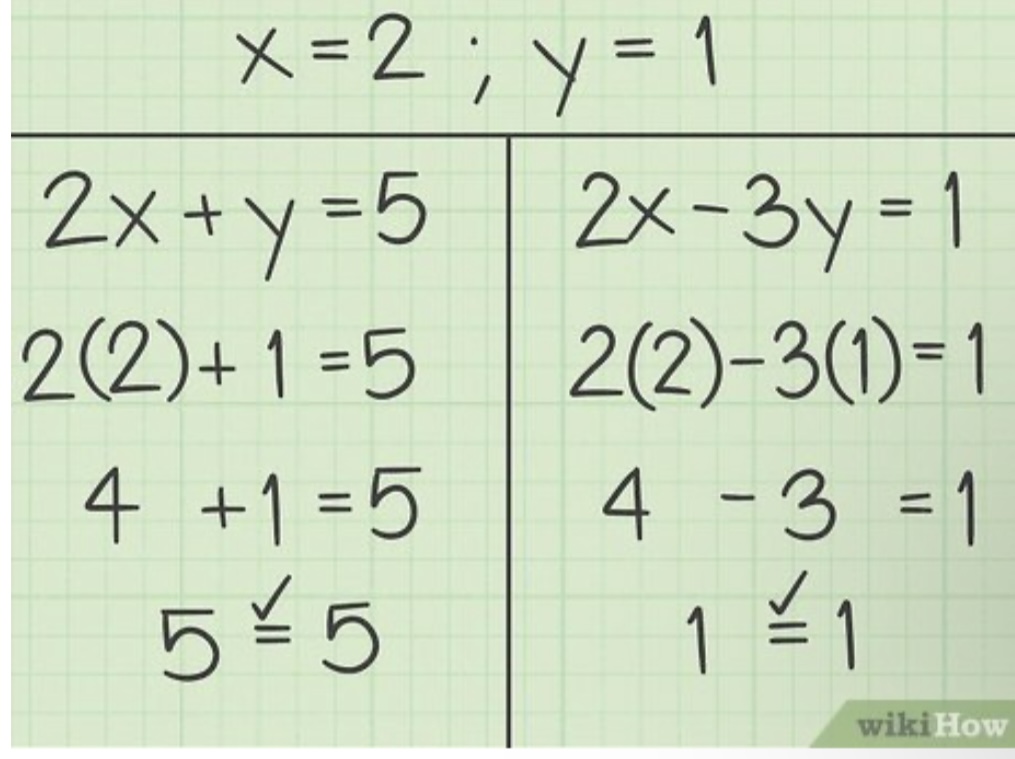
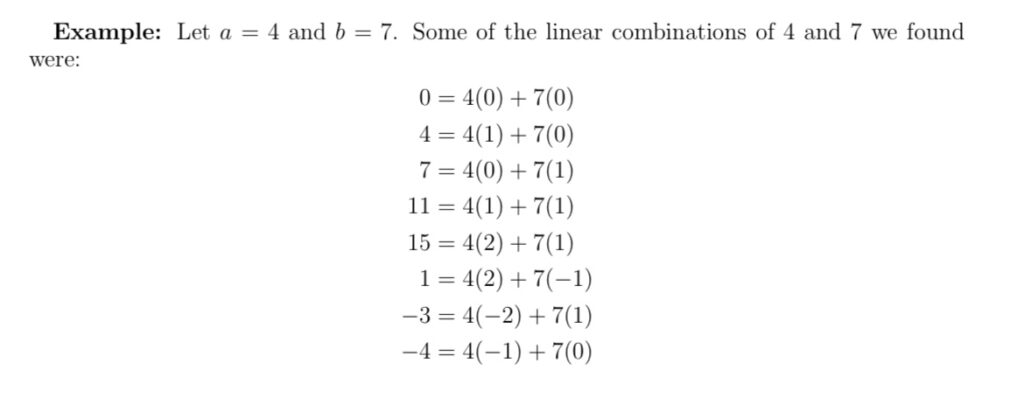



Leave a Reply