Lesson 17: Trigonometric functions

Hi everyone! Read through the material below, watch the videos, and send me your questions. Don’t forget to complete the Daily Quiz (below this post) before midnight to be marked present for the day.

Lesson 17: Trigonometric functions

Lesson Date: Tuesday, April 14th.

Topic: This lesson covers Chapter 17: Trigonometric functions.

WeBWorK: There are five WeBWorK assignments on today’s material, due next Tuesday 4/21:
Trigonometry - Unit Circle,
Trigonometry - Graphing Amplitude,
Trigonometry - Graphing Period,
Trigonometry - Graphing Phase Shift, and
Trigonometry - Graphing Comprehensive

Today we start trigonometric functions. We’ll begin with a review of the basics of trigonometry — if you remember everything about trigonometry, you can skip this part (but please don’t!). Then we’ll think about how these behave as functions, and look at their graphs.

Lesson NOtes (Notability – pdf):

This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.

Lesson 17_ Trigonometric FunctionsDownload

Review of trigonometry

a. Angles

We measure angles using two different systems, degrees and radians. In degrees, a full circle is $360^\circ$. In radians, a full circle is $2\pi \text{rad}$. Thus, we have $360^\circ=2\pi$ radians. If we consider a half-circle (divide both sides by two), we get:

$$180^\circ=\pi$$

Although most people are more familiar with degrees from their day-to-day lives, most mathematics at this level and above use radians. It will help you to get familiar with common angles in radians! The first video gives a review.

Why do mathematicians and scientists prefer radians to degrees? Great question!

VIDEO: Review of angles, radian measure

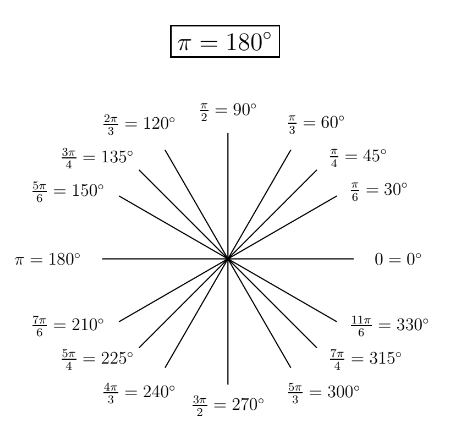
Common angles, in degrees and radians
Common angles, in degrees and radians.

b. Trigonometric Functions

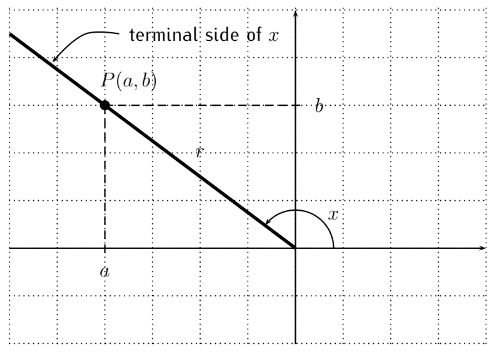
Definition. To define the trigonometric functions, we consider the following diagram: the initial side of an angle $x$ lies on the positive x-axis, and the terminal side of the angle passes through a point $P(a,b)$.

Diagram: Definition of Trigonometric Functions

The distance from the origin $(0,0)$ to the point $P$ is $r$ (note: if we know $a$ and $bg$ we can calculate $r$ by using the Pythagorean Theorem, $r=\sqrt{a^2+b^2}$). Then the trigonometric functions (sine, cosine, tangent, cosecant, secant, cotangent) of $x$ are defined:

$$\sin(x)=\frac{b}{r},\quad \cos(x)=\frac{a}{r},\quad\tan(x)=\frac{a}{b}$$
$$\csc(x)=\frac{r}{b},\quad \sec(x)=\frac{r}{a},\quad\cot(x)=\frac{b}{a}$$

VIDEO: Review – definitions of trigonometric functions

Next, we need to know the values of the trig functions for some common angles. Once again, this is a review of material from previous courses – the following video will take you through some examples, but for more details I recommend checking out the videos on our video resource page.

VIDEO: Values of trig functions at common angles

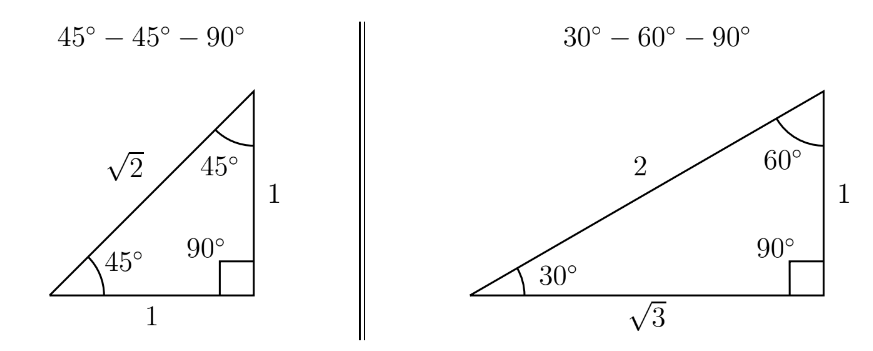
Special Triangles: These allow us to find the values of the trig functions at various common angles.
Special Triangles: These allow us to find the values of the trig functions at various common angles.
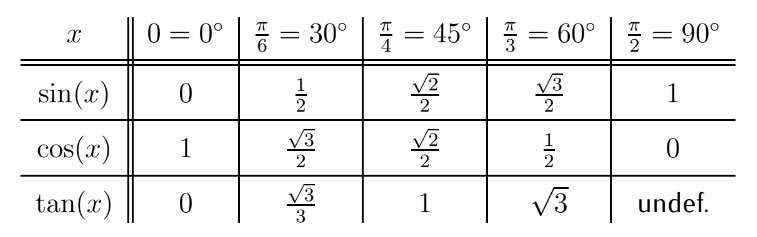
These are the values of sine, cosine and tangent for common angles in the first quadrant. Learn them, memorize them, get to know them!
These are the values of sine, cosine and tangent for common angles in the first quadrant. Learn them, memorize them, get to know them!

This is the end of the ‘review’ part of the lesson. Need a little more help? Take a look at the videos on our video resource page.

Graphs of trigonometric functions

Now we turn to the main idea of this lesson. We begin by looking at the graphs of the basic trig functions, $\sin x$, $\cos x$, and $\tan x$.

VIDEO: Graphs of basic trig functions

Example 17.8. Graph the following functions:
$f(x)=\sin (x)+3,\quad g(x)=4 \cdot \sin (x), \quad h(x)=\sin (x+2),\quad i(x)=\sin (3 x)$
$j(x)=2 \cdot \cos (x)+3, \quad k(x)=\cos (2 x-\pi), \quad l(x)=\tan (x+2)+3$

VIDEO: Example 17.8 modifying the graphs of trig functions – amplitude, period, phase shift.

Definition 17.9. Let $f$ be one of the functions:
$f(x)=a \cdot \sin (b \cdot x+c) \quad \text { or } \quad f(x)=a \cdot \cos (b \cdot x+c)$
The number $|a|$ is called the amplitude, the number $\left|\frac{2 \pi}{b}\right|$ is the period, and the number $\frac{-c}{b}$ is called the phase shift.

That’s it for now. Take a look at the WeBWorK, and send me your questions!

-Prof Reitz

Daily Quiz and Attendance: 4/14/20

Hi everyone,

Here is today’s Daily Quiz, based on the material covered in our last class.  As a reminder, the quizzes will count towards the OpenLab portion of your grade, and they will also be used to track your attendance (to be marked PRESENT, you must submit the quiz before midnight).

Today’s lecture will be posted later this morning.

As always, let me know if you have any questions or problems.  Stay healthy!

Prof.  Reitz

Daily Quiz: 4/14/20

This quiz MUST be taken on 4/14 to record your attendance.

  • An exponential function has the form f(x)=a*b^x. How many points (values of x and f(x)) do we need to know in order to find the numbers a and b?

Lesson 15-16: Applications of Exponential and Log Functions

Hi everyone! Read through the material below, watch the videos, and send me your questions. Don’t forget to complete the Daily Quiz (below this post) before midnight to be marked present for the day.

Lesson 15-16: Applications of Exponential and Logarithmic Functions

Lesson Date: Thursday, April 2nd.

Topic: This lesson covers Chapter 15: Applications of Exponential and Logarithmic Functions and Chapter 16: Half-Life and Compound Interest.

WeBWorK: There is one WeBWorK assignment on today’s material, due next Thursday 4/9: Exponential Functions - Growth and Decay.

We study exponential functions because they are amazingly good at describing real-world phenomena. Today we will look at several different applications of exponential functions, including population growth and virus spread.

Lesson NOtes (Notability – pdf):

This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.

Lesson 15-16_ Applications of Exponential and Log FunctionsDownload

Exponential growth and decay

RECALL: If $f(x)$ is an exponential function, then $f(x)=c\cdot b^x$.

NOTE: You can determine the values of $c$ and $b$ from any two points (input-output) on the graph.

Example 15.1.
a) $f(0)=4, \quad f(1)=20$
c) $f(2)=160, \quad f(7)=5$

Example 15.3 The population size of a country was $12.7$ million in the year 2000, and $14.3$ million in the year 2010.
a) Assuming an exponential growth for the population size, find the formula for the population depending on the year $t$ (where $t=0$ in the year 2000.
b) What will the population size be in the year 2015, assuming the formula holds until then?
c) When will the population reach 18 million?

You will often see exponential growth and decay functions written in a slightly different (but equivalent) form, using the number $e = 2.718…$ as a base. It’s also traditional to use $t$ (for time) instead of $x$ as our independent variable.

FACT. If $f(t)$ is an exponential function, then $f$ can be written as $f(t)=Pe^{rt}$. In this form:

  • $t$ represents time
  • $P$ is the initial amount
  • $r$ is the growth rate (if $r$ is positive, we have exponential growth, if $r$ is negative we have exponential decay)
  • $f(t)$ is the amount remaining at time t
  • $e=2.718…$

QUESTION: What’s the connection between $f(x)=c\cdot b^x$ and $f(t)=Pe^{rt}$?

Definition (exponential decay). The half-life of a substance is the time it takes for the amount to be cut in half.

EXAMPLE: A study published about two weeks ago, on March 17th, in the New England Journal of Medicine found experimentally that the half-life of the Covid-19 virus in the air is approximately 1.15 hours. A single cough by an infected person can release up to 6 billion coronavirus molecules into the air. Let’s consider what happens after a single cough by an infected person.

  • a. Model the number of remaining virus molecules $V(t)$ in the air at time $t$ by an exponential function $V(t)=Pe^{rt}$ (find $P,r$).
  • b. How many of virus molecules will remain viable 5 hours after the person coughed?
  • c. How long will it take for the number of remaining molecules to reach $6$ million ($0.1\%$ of the original amount)?

That’s it for now. Take a look at the WeBWorK, and send me your questions!

-Prof. Reitz

Daily Quiz and Attendance: 4/2/20

Hi everyone,

Here is today’s Daily Quiz, based on the material covered last Thursday.  As a reminder, the quizzes will count towards the OpenLab portion of your grade, and they will also be used to track your attendance (to be marked PRESENT, you must submit the quiz before midnight).

Today’s lecture will be posted later this morning.

As always, let me know if you have any questions or problems.  Stay healthy!

Prof.  Reitz

Daily Quiz 3: 4/2/20

This quiz MUST be taken on 3/26 to record your attendance.

  • No need to show your work, just give the answer. Typing math into a text box can be a challenge – do your best!

Lesson 14: Properties of Exponential and Logarithmic Functions

Hi everyone! This is the third of our distance-learning lessons. Read through the material below, watch the videos, and send me your questions. Don’t forget to complete the Daily Quiz (below this post) before midnight to be marked present for the day

Lesson 14: Properties of Exponential and Logarithmic Functions

Lesson Date: Thursday, March 26th.

Topic: This lesson covers Chapter 14 in the book, Exponential and Logarithmic Functions.

WeBWorK: There are three WeBWorK assignments on today’s material, due next Thursday 4/2: Logarithmic Functions - Properties, Logarithmic Functions - Equations, and Exponential Functions - Equations

Today’s goal is to review the properties/rules of exponents and logs, and then see how we can use them to solve equations.

Lesson NOtes (Notability – pdf):

This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.

Lesson 14_ Properties of Exponential and Logarithmic FunctionsDownload

Properties of Exponential and Logarithmic Functions

You should already be familiar with the rules of exponents and rules of logarithms. I realize you may not remember them, so read through the material below and take a look at the examples in the first video.

Review: Properties of Exponential Functions

The following rules apply to exponential functions (where $b>0$ and $x,y$ are any real numbers):

$b^{x+y}=b^{x} \cdot b^{y}$
$b^{x-y}=\frac{b^{x}}{b^{y}}$
$\left(b^{x}\right)^{n}=b^{n x}$

Review: Properties of Logarithmic Functions

The following rules apply to logarithmic functions (where $b>0, b\neq 1$ and $x,y > 0$, and $n$ is an integer).

$\log_{b}(x \cdot y)=\log_{b}(x)+\log_{b}(y)$
$\log_{b}\left(\frac{x}{y}\right)=\log_{b}(x)-\log_{b}(y)$
$\log_{b}\left(x^{n}\right)=n \cdot \log_{b}(x)$ 

Change of base formula (if $a>0, a\neq 1)$:  
$\log_{b}(x)=\frac{\log_{a}(x)}{\log_{a}(b)}$

Since the logarithm is the inverse of the exponential function, each rule of exponents has a corresponding rule of logarithms.

Example 14.1: Combine the terms using the properties of logarithms so as to write as one logarithm.

a) $\frac{1}{2} \ln (x)+\ln (y)$
b) $\frac{2}{3}\left(\log \left(x^{2} y\right)-\log \left(x y^{2}\right)\right)$
c) $2 \ln (x)-\frac{1}{3} \ln (y)-\frac{7}{5} \ln (z)$ 
d) $5+\log_{2}\left(a^{2}-b^{2}\right)-\log_{2}(a+b)$
Example 14.2:  Write the expressions in terms of elementary logarithms $u=$ $\log_{b}(x), v=\log_{b}(y),$ and, in part $(\mathrm{c}),$ also $w=\log_{b}(z) .$ Assume that $x, y, z>0$

a) $\ln \left(\sqrt{x^{5}} \cdot y^{2}\right)$
b) $\log (\sqrt{\sqrt{x} \cdot y^{3}}) \quad$ 
c) $\log _{2}(\sqrt[3]{\frac{x^{2}}{y \sqrt{z}}})$

Warning: The videos in this lesson are LONG – about 30 minutes each – but they consist almost entirely of EXAMPLES. Feel free to skip around.

Prof. Reitz

Solving Exponential and Log Equations

Now we’re going to use these properties to solve equations.

Example 14.5: Solve for $x$.

a) $2^{x+7}=32$
b) $10^{2 x-8}=0.01$
c) $7^{2 x-3}=7^{5 x+4}$
d) $5^{3 x+1}=25^{4 x-7}$
e) $\ln (3 x-5)=\ln (x-1)$
f) $\log_{2}(x+5)=\log_{2}(x+3)+4$
g) $\log_{6}(x)+\log_{6}(x+4)=\log_{6}(5)$ 
h) $\log_{3}(x-2)+\log_{3}(x+6)=2$
Example 14.6: Solving Log Equations

a) $3^{x+5}=8$
b) $13^{2 x-4}=6$
c) $5^{x-7}=2^{x}$
d) $5.1^{x}=2.7^{2 x+6}$
e) $17^{x-2}=3^{x+4}$
f) $7^{2x+3}=11^{3x-6}$

That’s it for today, everybody! Give the WeBWorK a try, and let me know if you have questions.

-Prof. Reitz

Daily Quiz and Attendance #2: 3/26/20

Hi everyone,

Here is today’s Daily Quiz, based on the material covered on Tuesday.  As a reminder, the quizzes will count towards the OpenLab portion of your grade, and they will also be used to track your attendance (to be marked PRESENT, you must submit the quiz before midnight).

Today’s lecture will be posted later this morning.

As always, let me know if you have any questions or problems.  Stay healthy!

Prof.  Reitz

Daily Quiz 2: 3/26/20

This quiz MUST be taken on 3/26 to record your attendance.

  • If you wish, you can give an example as part of your explanation (1 paragraph).

Coronavirus Update: Spring Break, Borrowing a Laptop/iPad

Hi everyone,

I hope you are well and safe during this extraordinary time. I’m writing with two updates:

  1. First, our schedule for the next few weeks has been updated by CUNY Central (this encompasses Spring Break). Take a deep breath and prepare to mark your calendars, it gets a little complicated!
    • NO CLASSES from this Friday, 3/27, through next Wednesday, 4/1. Classes resume on Thursday, 4/2. (According to CUNY, this is a “Recalibration period” which will be used to help ensure that all students have access to the technology they need for distance learning — see item #2 below if you need a laptop or iPad).
    • CLASSES RESUME next Thursday 4/2 (we will have class on Thursday 4/2), and continue until the beginning of Spring Break the following week.
    • TUESDAY 4/7 is a WEDNESDAY SCHEDULE, so we will not have class.
    • SPRING BREAK will take place from 4/8 to 4/10 (three days only!) – so we will not have class on THURSDAY 4/9. If you must miss class the following week for religious observances, please let me know ahead of time.
    • CLASSES RESUME after Spring Break, on Saturday 4/11 (our class will meet on Tuesday 4/14, as usual).
To recap, here is our schedule for the next few weeks:
– Thursday 3/26 we have class as usual, look for Lesson 14 on OpenLab.
– Tuesday 3/31 NO CLASS – CUNY Recalibration period
– Thursday 4/2 we have class as usual, look for Lesson 15 on OpenLab.
– Tuesday 4/7 is a Wednesday schedule, so our class does not meet.
– Thursday 4/9 NO CLASS – Spring Break
– Tuesday 4/14 we have class as usual, look for Lesson 16 on OpenLab.
  1. Do you lack the technology required to participate in Distance Learning? Check out this message from our Dean:
Dear student,

In the coming days we will be receiving a limited supply of Chrome Books and iPads to lend out to students who need them in order to continue their classes in this new online setting. They will need to be returned at the end of the semester. We want to be sure to get these to the students who most critically need them. Therefore, if you already have a laptop or desktop at home, or other resources to continue taking classes online, then please do not respond to this.

However, if it would be impossible or very difficult for you to continue online classes without receiving either a Chrome Book or iPad then please let us know by filling out this online survey right away. 

https://docs.google.com/forms/d/e/1FAIpQLSeXUALqOA_hJ7mjFjc28tJ-f-XnhCDD1pLBj_EgNrN4EuySMg/viewform

– Dean Justin Vazquez-Poritz

I wish everyone the best, and I thank you for your patience and adaptability as we navigate these unpredictable events. I will post a Daily Attendance Quiz as well as Lesson 14 in the morning.
-Prof. Reitz

Lesson 13: Exponential and Logarithmic Functions

Hi everyone! This is the second of our distance-learning lessons. Read through the material below, watch the videos, and send me your questions.

NEW THIS WEEK: Daily Quiz & Attendance. There will be a short quiz each class day. Complete the quiz before the end of the day to be marked present for today’s class (the quiz should appear below this post).

Lesson 13: Exponential and Logarithmic Functions

Lesson Date: Tuesday, March 24th.

Topic: This lesson covers Chapter 13 in the book, Exponential and Logarithmic Functions.

WeBWorK: There are two WeBWorK assignments on today’s material, due next Tuesday 3/31: Exponential Functions - Graphs and Logarithmic Functions - Graphs .

Lesson NOtes (Notability – pdf):

This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.

Lesson 13_ Exponential and Logarithmic FunctionsDownload

Exponential Functions and their Graphs

We’ve been living in the world of Polynomials and Rational Functions. We now turn to exponential functions. These functions are “very natural” – that is, they show up in the real world – but they are also more complicated than Polynomial and Rational functions (for example, an exponential function grows more quickly than any Polynomial)

The spread of coronavirus, like other infectious diseases, is modeled by exponential functions.

Definition. An exponential function is a function of the form $f(x)=c\cdot b^x$, where $b$ and $c$ are real numbers and $b$ is positive ($b$ is called the base, $x$ is the exponent).

Example 1 (Textbook 13.2): Graph the exponential functions $f(x)=2^x, g(x)=3^x, h(x)=10^x, k(x)=\left(\frac{1}{2}\right)^x, l(x)=\left(\frac{1}{10}\right)^x$.

Now let’s see what happens when we change the number $c$ in $y=c\cdot b^x$.

Example 2 (Textbook 13.6): Graph the exponential functions
a) $y=2^{x}, \quad$ b) $y=3 \cdot 2^{x}, \quad$ c) $y=(-3) \cdot 2^{x}, \quad$ d) $y=0.2 \cdot 2^{x}, \quad$ e) $y=(-0.2) \cdot 2^{x}$

Example 3: The graph below shows an exponential function $f(x)$. Find a formula for $f(x)$.

Logarithmic Functions and their Graphs

Definition. If $b$ is a positive real number and $b\neq 1$, then the logarithm with base $b$ is defined:
$y=\log_b(x) \iff b^y=x$

What does the definition of logarithm mean? The idea is that the logarithm is the inverse function of the exponential function. Let’s look at an example.

Question: Is an exponential function one-to-one? (What does one-to-one means).

Example 4. The graph below shows the function $y=\log_2(x)$ but shifted to the right 3 units. Find a formula for the function in the graph.

That’s it for now! Take a look at the WeBWorK assignment, leave your questions below (or use the Ask for Help button in WeBWorK, or send me an email) and don’t forget to complete Quiz#1.

Best of luck,
Prof. Reitz

Daily Quiz and Attendance #1: 3/24/20

Hi everyone,

For now, we are going to try out taking a quiz each class day, based on the material from the previous class.  The quizzes will count towards the OpenLab portion of your grade, and they will also be used to track your attendance (to be marked PRESENT on Tuesday, 3/24, you must take the quiz before midnight).

Today’s lecture will be posted later this morning.

As always, let me know if you have any questions or problems.  Stay healthy!

Prof.  Reitz

 

Daily Quiz 1: 3/24/20

Our first daily quiz. NOTE: This quiz MUST be taken on 3/24 to record your attendance.

  • You don’t need to do any calculations here, just describe how to do it (1 paragraph).

The OpenLab at City Tech:A place to learn, work, and share

The OpenLab is an open-source, digital platform designed to support teaching and learning at City Tech (New York City College of Technology), and to promote student and faculty engagement in the intellectual and social life of the college community.

Support

Help | Contact Us | Privacy Policy | Terms of Use | Credits

Accessibility

Our goal is to make the OpenLab accessible for all users.

Learn more about accessibility on the OpenLab

Copyright

Creative Commons

  • - Attribution
  • - NonCommercial
  • - ShareAlike
Creative Commons

top