Your assignment for the coming week+ is to try to prove the conjecture that your group created in class on Thursday, 10/25/15. You may need to refine/expand your conjecture first (let’s discuss this in class). You must spend at least 90 minutes working on this. Trying to prove something can consist of many different activities, such as the following (you do NOT have to do all of these things – you can choose how to spend your time – they are provided for inspiration only).
- coming up with ideas, and testing them out (for example, by creating puzzles and trying to solve them)
- trying to understand what the conjecture says
- trying to solve puzzles that other people created
- trying to create puzzles (and solve them yourself)
- communicating with other members of your group (talking, emailing, etc.)
- trying to write down a proof
- other stuff…
As you work, keep track of what you are doing, thinking, and feeling (this is metacognition – an idea that discussed way back in OpenLab #2). What did you do during the time you spent? Did you create any puzzles? Did you solve puzzles? Did you change your mind about whether the conjecture is true or false? Did you have any new ideas about how to prove the conjecture? Did you have any ideas that you gave up on? How did you feel as you worked – were you frustrated/confused/happy/depressed? Why? Did your mood change along the way?
Assignment (Due Tuesday, 11/6/15): Submit a journal of your efforts in the comments below. Your response should be at least 300 words. Describe what you did during the 90 minutes you worked, and express in some way what you were thinking and feeling during the process. Your response can include puzzles (use sketchtoy.com) or other work you did along the way.
Extra Credit. Respond to a fellow student’s comment. Did you do similar things? Different things? Do you have any suggestions for them? Be kind.
GROUP CONJECTURES (created in class 10/25):
Group 1: Federico, Samantha, Yvan
Group 2: Jess, Young, Rachel, Alex
Group 3: Danping, Franklin, Silvana, Jessie

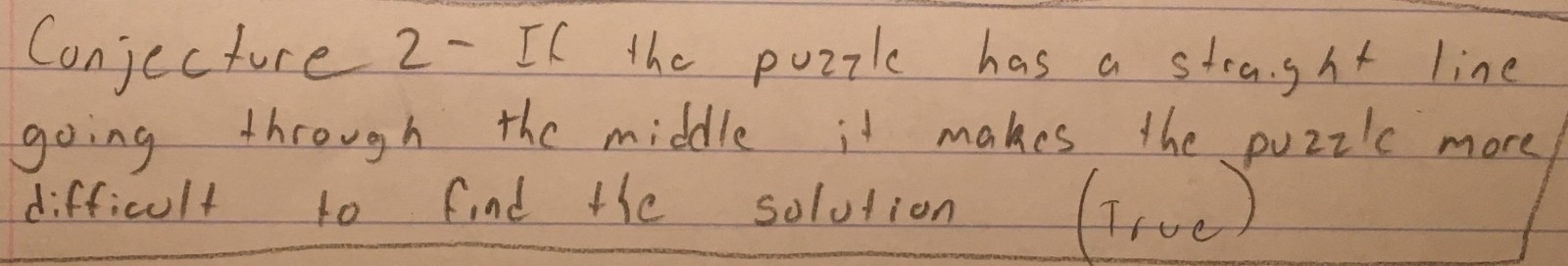
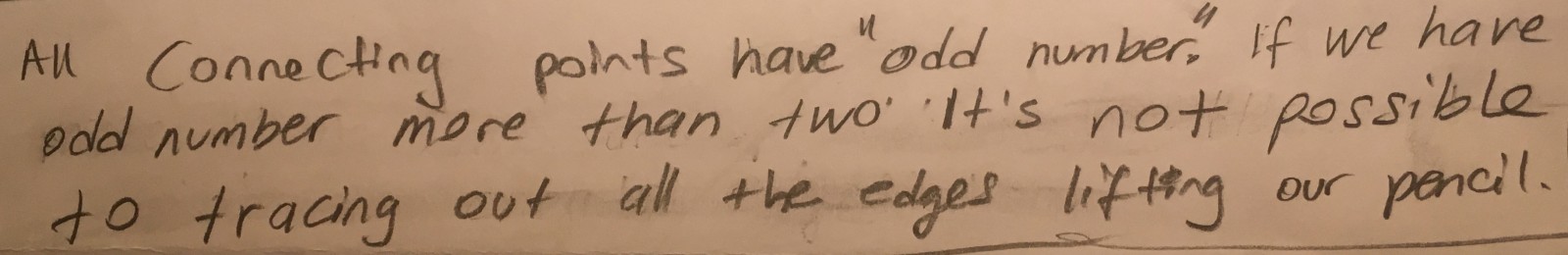
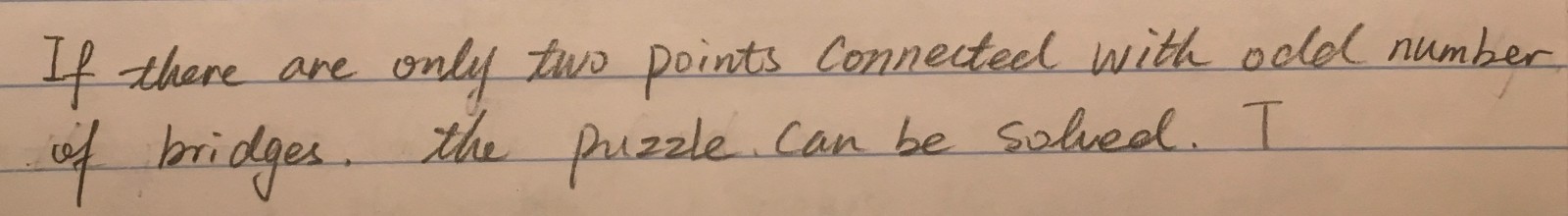



Solving this puzzle kept me busy because when I start something, I need to finish it. I tried to solve this puzzle many times without giving up because I knew that there had to be a solution. In class, we have learned how to prove that an even or odd number. I noticed that this puzzle had a connection with even and odd numbers. The bridge had only four connecting points, so I started to count how many possible ways there were to go to each point. I figured out that the A, B, and D points had only three ways to go out, and C had five points. I observed that all points had an odd number. Then I went to count the puzzle “G4,” where I also found that A, C, D, and E had only three ways to go on, and B and F had four. I also looked at the other puzzles, G1, G2, and G3, and I saw that G1 and G2 had only two odd numbers, and the rest of the connecting points were even numbers. The G3 connecting points didn’t have any odd numbers. I shared my findings with the group. It was interesting to hear other people’s ideas. Rachel thought about geometry, which was interesting. She said, “if a puzzle is made up of only one square, then it will always be solvable.” I thought this conjecture could also be true. After a group discussion, we decided to choose my conjecture to prove it. That week, I started to think how I could prove this conjecture is true. Then I wondered about my classmates’ puzzles, and I counted them. When I was trying to solve my classmates’ puzzles, I found that Rachel’s puzzle was unsolvable because it had only one odd number. Then, I emailed her to ask, “How can I solve this puzzle? (https://sketchtoy.com/68770750)” She told me that there was no solution for it, so I concluded that if the puzzle’s connecting points have more than two odd numbers, then the puzzle cannot be solved. If this is true, we can save time and don’t have to draw and waste paper to figure out the solution. We only need to count how many connecting points there are, and if the connecting points have more than two odd numbers, then we know that the puzzle is unsolvable.
The conjecture that my group chose to work with was Jess’s idea that if a puzzle contains more than two points where there are an odd number of connections, then that puzzle is unable to be solved. We chose this conjecture in part because so many proofs we’ve done in class have taken into account the parity of a number and we felt it might make proving the statement more feasible. In order to go about proving this, I looked back through the puzzles submitted on the OpenLab and took note of which ones could be solved and which couldn’t. From my work, I found that our conjecture was holding up. The puzzles that I decided could not be solved were the ones with more than two odd numbers. I then decided to try and draw my own and see if I could create one that would go against our conjecture, similar to the existence proofs we did in class. I figured it might be easier to try and find a puzzle that would disprove our conjecture than test every puzzle I come across that meets the conditions. I drew a few simple puzzles that had more than two odd numbers and could not create one that could be solved. I then drew some more complicated puzzles and found that they still could not be solved. I think that our conjecture is strong and will be proved true, however, other than testing puzzles and creating new ones, I am not sure how else we can go about proving it. It seems like Group #3 has the same conjecture as our group, so it would be interesting to see how they try to prove it. I find it interesting that while worded differently, our conjectures are more or less the same, and wonder if it’s easier to prove that a puzzle can be solved than trying to prove that a puzzle cannot be solved.
“If there are only two points connected with odd number of bridges then the puzzle can be solved”
Although we had discussed the conjecture in class. Every time I read the conjecture out Loud I got somewhat confused on what exactly the theory was implying. So first I tried to analyze the conjecture to understand it entirely. So I drew a puzzle randomly drawing and connecting lines, my puzzle resulted in ten lines with seven points joining them. I then color coded each point. using the same color I numbered the lines connecting each point so I wouldn’t get lost or confused. Five of my points had three bridges connecting them, two of them had two bridges connecting. With this visual I then had a complete understanding of what the conjecture said but based on the conjecture my puzzle couldn’t be solved because I had more than two points connected with odd number of bridges; I had five. So I tried to solve my puzzle, after multiple attempts I realized I couldn’t . I then decided to draw a simpler puzzle, this time my goal was to make sure only 2 of my points had an odd number of bridges. The result was a puzzle with 6 lines, and 5 points. 2 points had an odd number of points connecting and the 3 had 2. I solved the puzzle in less than thirty seconds. I then started to build on this puzzle making sure to keep only 2 points with an odd number of points. I added six lines and three point. My previous points which had an odd number of bridges connecting them now had an even number and two out of three of my points that previously had an even number connecting now had odd. Although it took a little longer this puzzle also had a solution.The more I added to this puzzle with caution to keep only to points with an odd number of bridges connecting the more difficult it became to solve but still, I was able to solve it. In conclusion, I randomly added one line and one point to an evenly connected point. My last puzzle had 3 points with an odd number of bridges and again was unsolvable. Based on my own puzzles I couldn’t prove our conjecture wrong.
My group conjecture is that “if the puzzle has a straight line going through the middle it makes the puzzle more difficult to find the solution”. We first thought that no matter what puzzle has a line going through it we cannot solve it at all. The main reason why we thought this was because of the game creating walking tours of cities with bridges, in the city of King’s Mountain. This puzzle has no solution, no matter how many different ways you start the line going through the puzzle makes it very difficult to find a solution. Also, there is a puzzle that I came up with for one of the open lab homework where it had a line going through and it didn’t have a solution http://sketchtoy.com/68792480 . So, we thought that out first theory was true no matter what if there is a line going through it. But, Federico remembered a puzzle that had a line going through it and it had a solution http://sketchtoy.com/68792487. So, we had to change our conjecture to what it is now. The line going through the puzzle just makes it more difficult to solve. We had to keep testing puzzles, because we then found out that our first conjecture about a line going through the puzzle never has a solution was not true. Here is another puzzles that don’t have a solution http://sketchtoy.com/68792479 , it looks easy to solve but its truly not. What I did do during my time spent was that I kept trying out other puzzles to make sure that our final conjecture is true and it is. While doing the puzzles I was a bit excited to find another puzzle that has a solution with a line going through it. I just kept finding some with no solution. I’m going to asks my group members about what other puzzles they try to solve that has a solution to it.
I drew the same puzzle that you did with one fewer connection point. What I found was that after taking out connection point D, three connection points were left: A, B, and C. Then I started to count each of the three connection points to determine how many possible ways there were to go on. I found that A and B have three, and C has five. So we had three odd numbers, about which our group said, “If the connection points have more than two odd numbers, it’s unsolvable.” I think you also said that “http://sketchtoy.com/68792479” this puzzle was unsolvable.
Our group conjecture is “If there are only two points connected with odd number of bridges, the puzzle can be solved.” It means if a puzzle has only two points are connected with odd number of bridges, such as in puzzle 1, the points A, B, C, D are connected with 3 bridges, and that’s odd number of bridges. But there are 4 points connected with odd number of bridges. So it doesn’t fit the condition of our conjecture. Our conjecture can not determent if it can be solved or not. In Puzzle 2, point A, B are connected with 2 bridges, point E, J are connected with 3 bridges, and other points are connected with 4 bridges. So there is 2 points connected with odd number of bridges. It satisfies the condition of our conjecture. So if our conjecture is true, we can find a solution for it. And in fact, I did find a solution.
I tried to use our conjecture to test some puzzles. In OpenLab #4, all of us can find a solution for G1-G3 puzzles, but couldn’t find a solution for G4. So I test those puzzles with our conjecture. G1 and G2 satisfies our condition, and they all can be solved. I also used it to test the puzzles created by our group members. One of them looks complicated, but it fits the condition of our conjecture, and I can find a solution for it. Our conjecture seems true by testing some puzzles.
Why it’s true? And how can I proof it’s true? First, I think I need to be clear that our conjecture has a condition. I need to focus on this condition. When I was testing the puzzles with our conjecture, I also found that I couldn’t find a solution for those puzzles with 4 points connected with odd number of bridges. Then I fell into the thinking of why those puzzles have no solution. And I also found that if a puzzle with all points connected with even number of bridges, they can be solved. They maybe have some connection with our conjecture, but I’m not sure yet. Second, I notice some facts that maybe helpful for proof: 1. Every point is connected with even or odd number of bridges. 2.Each bridge is connected with two points. 3.Since when we passing a point, there must be an enter and exist. So the points connected with even number of bridges can be starting point, ending point or middle point. But the points connected with odd number of bridges has to be starting points or ending points.
I think I need to think about more facts in order to proof it. And I may use direct proof or contradiction.
This two puzzles were created by Rachel in OpenLab #4. (Thank you Rachel
Puzzle 1. https://sketchtoy.com/68770750
Puzzle 2. https://sketchtoy.com/68770754
G1-G4 Puzzle:
https://openlab.citytech.cuny.edu/2018-fall-mat-2071-reitz/files/2017/09/EulerPathsG1-G4.png
Our group used the conjecture; “if there are only two points connected with an off number of bridges, then the puzzle can be solved.” When I first heard this conjecture, I had a difficult time understanding what it meant. Only after reading it over many times and drawing several examples, I slowly began to understand the conjecture. That In order to determine whether the conjecture is true the puzzle must have a solution that has to includes two points that are connected with an odd number of bridges. To comprehend the conjecture better, I started with a simple drawing. Then I used the drawing as an example, to show that this conjecture can be true. The drawing was of a square with a diagonal line. The square had two corner points with have three bridges; and if you start from either of those two points, the puzzle will be solved. I then tried another example, it was of pentagon with another diagonal line in the square. Out of those five points, the pentagon has two points have three bridges and one point has four bridges. Afterwards, I tried variety of different ways of solving this puzzle. After many unsuccessful attempts, I saw that there were only six different ways of starting the puzzle and then I began trying to solve it. The six-different ways began from the two points that contained three bridges. Then I tried to begin from a point that has four bridges. However, I was not able solve the puzzle beginning from a point with four bridges. By using different examples, I was able to understand the conjecture in a much clearer way. I used simple puzzles, so it was easy for me to understand. From there, I added to the puzzles but keeping the same rules.
My groups conjecture is “if the puzzle has a straight line going through the middle it makes the puzzle more difficult to find the solution”. At first we thought have a straight line through the puzzle made it impossible to solve because of the kings mountain puzzle. We noticed that the reason we couldn’t solve it was because the puzzle had a straight line going through the middle. In other words it has a line bisecting the puzzle and making it symmetrical. We could not find a solution. Then through drawing various puzzles with a line going through the middle and bisecting the puzzle we noticed that some did have solutions and others had no solutions. So we decided to say a line going through the middle makes it more difficult. We later drew a couple more puzzles to show which we find difficult and easy. I think in order to prove our conjecture we will have to make a clear definition for what it means to be a “Difficult” puzzle, and we also have to define what an “Easy” puzzle is. But that’s a bit easier said than done because I feel like there will always be a puzzle that doesn’t agree with our definition. What I did during my time spent, was to come up with a clear and not so broad definition of what it means to be a “Difficult” puzzle. The best I could come up with was, “To be a difficult puzzle, the puzzle must have only 2 or less ways to solve the puzzle, or have no solution at all”. I guess what that means is you can’t just start at any given point of the puzzle. In order to solve a difficult puzzle there must be 2 or 1 key points to start off or you won’t reach a solution. I hope somehow we can work from my groups ideas and my ideas.
During the group activity we tried to simplify our conjecture. We read and reread our conjecture to make sure it made sense to the group and to make sure it would make sense when we explained it. Once we were all on the same page in understanding we began to experiment. We started to draw pictures to try and find our conjectures limitations. We figured out that we need to have an even amount of lines per path in order to find the solution. If there was more than two odd paths then we could not solve out problem. Upon further practice we found that by manipulating our image to add or subtract lines creates a solution to the original path that did not have one
There was a puzzle in class that we were asked to solve: “The Walking Tour Problem”. We had to visit all the areas by crossing each bridge at least once. We tried different methods and strategies to solve this puzzle. When we could not solve this puzzle, we had to understand why. We were grouped into teams of 3 or 4. In my group there were 4 students. We started constructing different types of puzzles to understand the walking tour and why there is no solution to “The Walking Tour Problem”. By constructing and solving, we came up with a conjecture: “If there are only two points connected with an odd number of bridges, then the puzzle can be solved.” Danping, my group member, discovered this conjecture. When Danping talked about her conjecture, I was confused about the meaning of two odd points connected. When she gave us an example of puzzles with her conjecture, I began to understand her conjecture. Then, I began to wonder if this conjecture can work with any puzzle. I began to construct puzzles which fit the conjecture. There were homework puzzles which our professor gave us to understand the walking tour challenge. Some of them have no solution. I wanted to see if our conjecture can work with those puzzles. So, I revisited the homework problem and discovered our conjecture was limited to those puzzles with two odd numbers of points (odd number 3) and the rest of the points are even. I came up with the idea that if there can be infinite numbers of even points and we cannot construct infinite number of even points, then I cannot say with certainty that the conjecture is proved. But based on all my puzzles I constructed and solved with our conjecture so far, I cannot disprove it.
Those are puzzles which meet our conjection:
http://sketchtoy.com/68832144
http://sketchtoy.com/68832149
http://sketchtoy.com/68832155
http://sketchtoy.com/68832162