In 2002, a mathematician named Paul Lockhart wrote an essay called “A Mathematician’s Lament,” a passionate criticism of mathematics education in America. It has become widely known among mathematicians and mathematics educators – not everyone agrees with everything he says (though many do), but everyone seems to have something to say about “Lockhart’s Lament,” as it is called. For this week’s assignment, you will read a short excerpt (three pages) from his essay and respond to the prompts below.
Assignment (Due Thursday, 10/18/17). Your assignment has three parts:
First, read the section titled “Mathematics and Culture” (pages 3-5) in Lockhart’s essay, (click here). If you’re interested, I encourage you to read more, starting at the beginning – but this is not required.
Second, write a response to what you read and post it in the comments below. Your response should be at least 300 words. Your response should represent your own thoughts and opinions on what you read, and can include responses to any or all of the following:
- What is one thing that you agree with in the reading? Explain why.
- What is one thing that you do not agree with? Explain.
- Choose one quote that you think stands out in the reading. Give the quote, and explain why you chose it.
- Have you ever had an experience of mathematics as art?
- On page 5, Lockhart describes mathematics in schools today as “heartbreaking”. What do you think he means? Do you agree? How do your own math experiences in school compare to his description?
Third, and most important, I want you to write down a conjecture about the Bridges and Walking Tours game, and bring it with you to class on Thursday 10/18 (do NOT post it here). Consider Lockhart’s example of a triangle drawn inside a rectangle. He described the process of playing around with this picture, until he arrives at the basic idea for calculating the area of a triangle. He contrasts this with a traditional math class, in which the formula is given to students without providing them any opportunity to explore the problem on their own. The bridges and walking tours game is a little like the triangle-rectangle picture – it’s fun to play around with, but you may not be sure what the point is. You’ve had a chance to play with it a bit, and try some different challenges. Now what? Your job is write down a conjecture (a guess!) or a question about your game. If you could have one question answered about your game, what would it be? If you wanted to be a master of your game, and be able to solve any challenge that was given to you, what would you need to know? Write down a conjecture or question about the bridges and walking tours game, and bring it with you to class on Thursday 10/18 (do NOT post it here).
Here is an example: Let’s imagine that you have just been introduced to the game Tic-Tac-Toe. After playing it for a while, you might come up with one of the following conjectures about Tic-Tac-Toe:
Conjecture: The person who goes first always wins.
Conjecture: The center is the best move.
Conjecture: It’s impossible to win, no matter who goes first.
ps. Paul Lockhart retired from being a first-rate research mathematician in order to teach math at a private elementary school here in Brooklyn, Saint Ann’s School, where he says “I have happily been subversively teaching mathematics (the real thing) since 2000.”

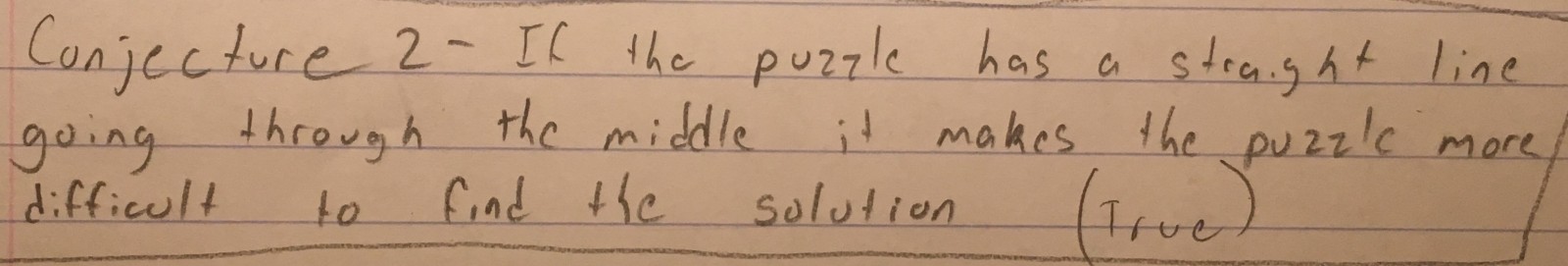
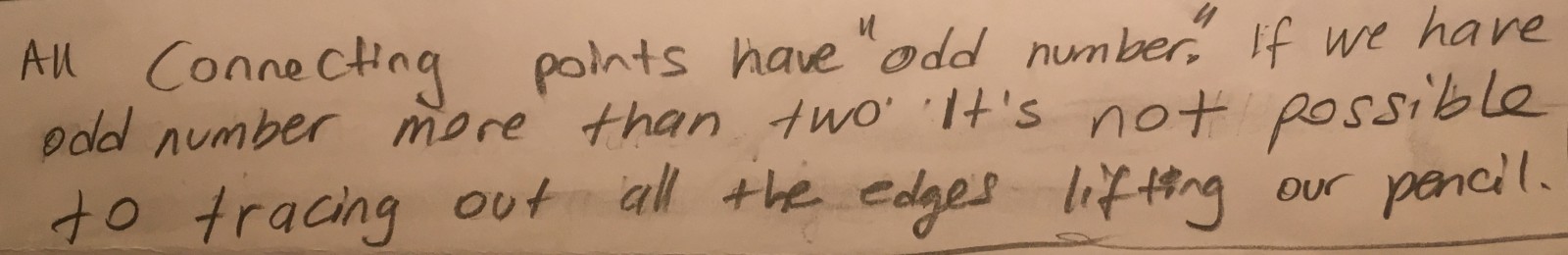
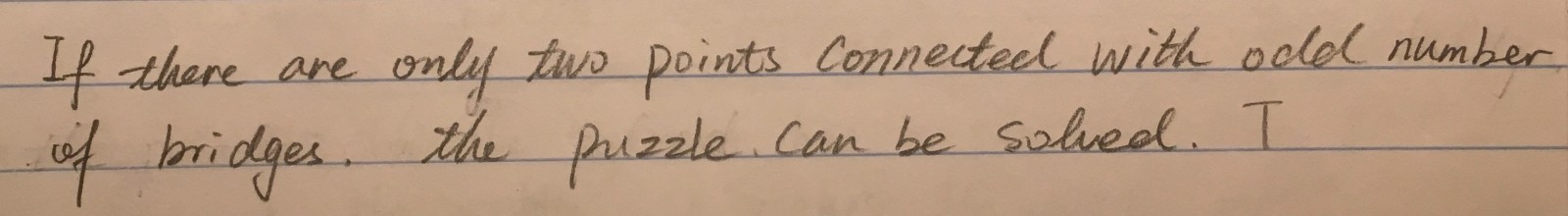



Recent Comments