Written work, Due Tuesday, October 23, in class:
Chapter 4 p.100: 4, 5, 10, 11
Chapter 5 p.110: 1, 4, 9
Odd problems are worth 4 points, even problems worth 8 points.
WeBWorK – none
OpenLab – none
Category: Assignments (Page 2 of 3)
Group Activity (25 min). Get into your groups (group assignments appear below), arrange your chairs in a circle, and take 25 minutes to:
1. Share your responses to OpenLab #4. Compare your answers to the given examples (do you all agree on the solutions?). Now share your own puzzles with the group, and discuss.
2. Create three new puzzles, as tricky as possible (try to stump Prof. Reitz!).
Group work due after 25 minutes: Each group will hand in a sheet of paper with the names of the groups members, the date, and the three new puzzles created by the group. You do not need to submit solutions, but you do need to be able to solve the puzzles on request.
Reflection: To be completed individually after group work is complete, and submitted on paper with your name and the date. Take 5 minutes to write on the following prompt:
Briefly reflect on the process of working in a group by responding to each of these points:
1. Describe something you learned.
2. Describe something you contributed to the group.
3. How did today’s work change your understanding of your assigned game?
Group Assignments
Group 1: Federico, Samantha, Jaroslav, Yvan
Group 2: Jess, Young, Rachel, Alex
Group 3: Danping, Franklin, Silvana, Jessie
UPDATE: In order to keep pace with our Semester Project, OpenLab #5 will be assigned on Thursday 10/11 and due next week Thursday 10/18.
Written work, Due Tuesday, October 16th, in class:
Chapter 4 p.100: 1, 6, 7, 15, 16
Odd problems are worth 4 points, even problems worth 8 points.
WeBWorK – none
OpenLab – OpenLab #5. NOTE: Please complete the writing portion on the OpenLab, but bring your Conjecture to class on 10/18 (do not post your Conjecture to the OpenLab)
The assignment below is due BEFORE CLASS on Thursday, October 11th (it is essential that you complete it before class, as we will be doing a class activity building on the assignment).
We are going to play a game creating walking tours of cities with bridges. We begin in the city of King’s Mountain, which is built on four land masses – both shores of a river and two islands in midstream – connected by a total of seven bridges (shown in green).
EXAMPLE 1: Can you create a walking tour of the city that crosses every bridge exactly once? You can begin anywhere you like, and end anywhere you like, as long as you cross each bridge just once.
Background – Graph Theory
We can simplify the picture of King’s Mountain to make it easier to deal with:
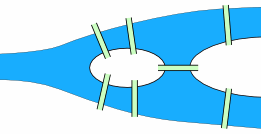
The key elements of the map are the four land masses (let’s label them A, B, C, and D) and the seven bridges (p,q,r,s,t,u and v) (thanks to mathisfun.com for the images):
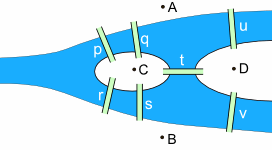
For the purposes of our problem, we can simply think about each land mass as a point (A, B, C, and D), and the bridges as lines connecting the points (p,q,r,s,t,u and v) – like this:
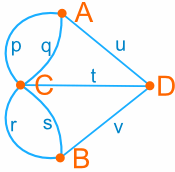
We call this kind of picture a graph – the points are called vertices and the the lines are called edges. Our goal of finding “a walking tour that crosses each bridge once” is now matter of tracing out all the edges without lifting our pencil (and without repeating any edge).
Assignment, Due Thursday 10/11 (beginning of class)
Warm up (This Warm Up is just for practice – you do NOT need to submit your answers – see below for the three-part Assignment to be submitted). The following examples build on the example above.
EXAMPLE 2: If you are given the freedom to build one new bridge in King’s Mountain (“make one new edge in the graph”), can you do it in such a way the walking tour becomes possible? Do it!
EXAMPLE 3: If you are given the freedom to destroy one bridge (“erase one edge”), can you do it in such a way that the walking tour becomes possible? Do it!
EXAMPLE 4: Construct walking tours for each of the following graphs (or decide if it is impossible).
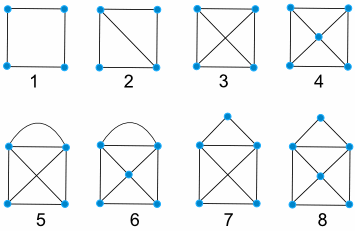
Assignment. Your assignment has 4 parts.
PART 1. For each of the four graphs below (G1 – G4), decide whether it is possible to create a walking tour crossing each bridge exactly once. Post your solutions here (TO POST A SOLUTION, JUST LIST THE POINTS OF YOUR WALKING TOUR IN ORDER). If it is not possible to create a create a solution, say so!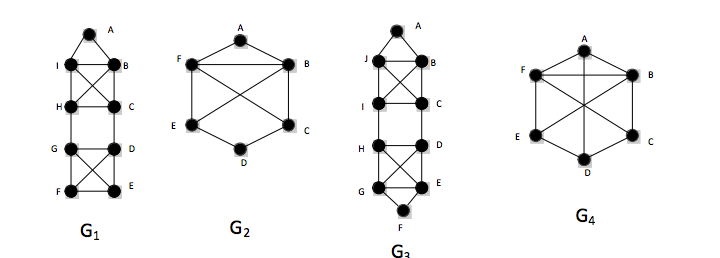
PART 2. Challenge your friends: Now it’s up to you to build your own graph, and challenge your classmates to construct a walking tour (or to determine if it is impossible). It can consist of as many points as you wish, and as many bridges (edges) connecting them. You MUST label your points “A, B, C…” etc. When you’re finished, decide for yourself if a walking tour crossing each bridge exactly once is possible. Remember, the most challenging puzzles are the ones where the answer is difficult to determine. Post two puzzles in the comments. See the note “POSTING YOUR PUZZLE ONLINE” below for instructions on how to draw and share graphs online.
PART 3. Solve a friend’s puzzle. Leave a response to a friend’s posted puzzle, giving a solution. TO POST A SOLUTION, JUST LIST THE POINTS OF YOUR WALKING TOUR IN ORDER.
Example:
Here is a puzzle: http://sketchtoy.com/67467551
Here is a solution: (start at A) – A, B, D, A, E, B, C, E
PART 4. The third part of your assignment is to write a short paragraph (at least 3 sentences) responding to the following prompt. Be sure to respond to each part:
Writing Prompt: Did you enjoy this assignment? Why or why not? Describe a connection between this assignment and our work in the class. (If you don’t believe there is a connection, try to imagine why we are doing this). Leave your response in the comments.
POSTING YOUR PUZZLE ONLINE. I recommend the site sketchtoy.com – it allows you to draw something, then click “SAVE” and get a link to your drawing. You can post the link in a comment, and we’ll be able to click on it and view your drawing. Don’t worry if it’s not pretty! For example, here is a graph that I drew (can you find a walking tour that crosses all edges?): http://sketchtoy.com/67467556
Written work – None.
WeBWorK – Assignment #5, due Tuesday, October 9th, at midnight.
OpenLab – OpenLab #4, due Thursday, October 11th, before class.
Week 5 Assignments
Exam #1 will take place on Tuesday, 10/2 (first half of class).
Written work – none
WeBWorK – Assignment #4, due Tuesday, October 2nd, at midnight. You are encouraged to start working on Assignment #5, which will be due one week later.
OpenLab – none
Week 4 Assignments
Written work – none
WeBWorK – Assignment #3, due Tuesday, September 25th, at midnight.
OpenLab – none
STUDY – for your first exam, taking place on Tuesday, 10/2, during the first hour of class. A review sheet will be posted at least 1 week prior to the exam.
Week 3 Assignments
Written work – None
WeBWorK – Start on WeBWorK 3, (it will not be due until Tuesday, 9/25 at midnight).
OpenLab – OpenLab #3, due Tuesday, 9/20 (at start of class).
NOTE: Next week Tuesday 9/18 there are no classes.
This assignment is due Thursday, September 13, at the start of class.
Assignment. Choose ONE of the following two topics. Write a reply to this post, responding to the topic. Begin by telling us which topic you chose. (1-2 paragraphs).
Topics.
- Sometimes people can recognize a time when their opinion of math dramatically changed either for the better or the worse. If such a time happened to you, tell us about it.
- Choose an experience you had in which you suddenly understood a math concept (it could be any kind of math, from elementary school up through college). Describe what happened. Do you think you could explain it to others in a way that they could have the same flash of understanding?
Extra Credit. For extra credit, write a response to one of your classmates’ comments. Do you feel the same, or different? Did you learn anything? Did you get any ideas about teaching, or about learning?
Why are we doing this, anyway? We are following two ideas that have come up already in class — things that may not seem related to learning math, but research shows that engaging in these activities can dramatically increase the amount that you learn, and change the way you learn it. The first is writing – something not typically associated with mathematics. When you express your ideas in words, it forces you to think them through very carefully, detail by detail. A great way to check and see if you really understand something is to try to explain it to someone else, either out loud or in writing. Example: if you know how to add fractions, try teaching it someone who doesn’t know how. The second is called metacognition, or “thinking about thinking.” This happens when you think about what was going on in your head while you were working on a problem or trying to learn a new idea. What train of thought did you follow? Where did you get stuck, and what did you do next? What were you feeling at the time? and so on. Combining writing and metacognition can be a tremendously powerful tool in identifying the ways we learn best and the ways we make mistakes, and learning to improve. However, like any skill, it takes practice. That’s why we’re getting started by writing a little about our past experiences with mathematics.
Week 2 Assignments
Because we do not have class on Tuesday, September 11th, all assignments will be due on Thursday, September 13th, this week.
Written work – Sec 1.8 p.28: 3, 5, 6, 8, Due Thursday, September 13th, at the start of class.
NOTE: On this assignment, odd problems are worth 3 points, even problems worth 5 points.
WeBWorK – Assignment #2, dueThursday, September 13th, at midnight.
OpenLab – OpenLab #2, dueThursday, September 13th, at the start of class.
Logic on Math StackExchange
- Explicit geometric machinery to check the truth of FOL formula April 25, 2024It is standard to use the semantics of topological spaces for checking the truth value of propositional formula in the absence of excluded middle. An explicit description is written down here, for example. https://grossack.site/2022/04/17/geometry-and-logic I suppose, there might be possible to have something similar to determine the truth value of first order formulas. i.e. There […]Y.X.
- Why is Gödel's Incompleteness Theorem relevant to anything beyond self-referential statements? April 24, 2024I feel like I understand the general idea behind how Gödel used self-reference to prove that there will always be holes in logical systems, even if you add the self-referential statement to the axioms because you can always create another statement that is true but cannot be proven via Cantor's diagonalization proof. I am confused […]user34140
- Examples of geometric theory without classical models April 24, 2024I encountered a post on locales and geometric theory here https://grossack.site/2022/05/22/locale-basics.html In about the middle of this blog, the author gives a geometric theory defining a function from $\Bbb N$ to $\Bbb R$, and asked: Do you see why this is a nontrivial theory with no classical models? I am not confident that I understand […]Y.X.
- can somone help me finish this fitch proof? [closed] April 24, 2024Premise 1: $P \to Q$ Premise 2: $\lnot P \to R$ Premise 3: $\lnot Q$ Goal: $R.$ $\def\fitch#1#2{\quad\begin{array}{|l}#1\\\hline#2\end{array}} \fitch{~~1.~~P\to Q\\~~2.~~\neg P\to R\\~~3.~~\neg Q}{\fitch{~~4.~~\neg R}{\fitch{~~5.~~P}{~~6.~~Q\hspace{10ex}{\to}\text{Elim }5,1\\~~7.~~\neg Q\hspace{9ex}\text{Reit }3\\~~8.~~\bot\hspace{10ex}\bot\text{Intro }6,7}\\~~9.~~\neg P\hspace{12ex}\neg\text{Intro }6{-}8\\10.~~R\hspace{13ex}{\to}\text{Elim }9,2\\~}\\~}$ the book is Language, Proof and Logic The Second Edition authors are Jon Barwise and John EtchemendyAvrgDude
- Question relating isomorphisms and structures in logic April 24, 2024A question in a sheet was as follows: Let $T_n,$ $n \in\mathbb N \setminus 0,$ be the structure $⟨N; f_n)$ where $f_n(a) = \lfloor\frac{a}{n}\rfloor.$ Draw a picture of Tn for n = 1, 2, 3. For T1 I drew a number-line from 1 to infinity For T2 I drew a number-line of 0, 1, 1, […]Alice
- Derivation of the "Chain syllogism" rule in first order logic April 24, 2024I'm currently reading these: https://www.mcmp.philosophie.uni-muenchen.de/students/math/math_logic_munich.pdf lecture notes and am kind of stuck on the proof on page 58 line 4 where $$\Gamma \lnot \varphi \lnot \varphi$$ is derived using (Ass.). I don't understand how, none of the rule thus far introduced allow me to manipulated the consequent except contradiction which I can't use in this […]Fabio
- Does “false” imply “true”? [duplicate] April 23, 2024I think calling a proposition an "implicature" means something like this: If there is a proposition "p->q" and this proposition is true, then we think that p "implies" q. So if p is false and q is true, does “false” imply “true”? My own thoughts are, Premise: ((I am a cup) and (the cup is […]Display name
- Show that Proof by Contradiction rule is derivable from all instances of it with atomic conclusion April 23, 2024The problem shows up in Troelstra's Basic Proof Theory, exercise 2.3.6A. Show that in [classical logic's Natural Deduction], for the languages without ∨, ∃, all instances of ⊥c derivable from instances ⊥c with atomic conclusions. I have a solution to the problem, but I'm not sure if it's correct as it seems trivials, perhaps because […]confusedcius
- Define something based on the property of another set. April 22, 2024I have always been confused about a logic problem, which I can not form it into a general statement. Here is an example that may express my ideas. We know given a set $A$ and an equivalent relation $\sim$ on it. We can define equivalence class by $\forall x\in A, [x]=\{y,|y \sim x\}$. It seems […]Andrew_Ren
- Prove $\forall x \forall y(xEy \rightarrow \neg x=y)$ in the vocabulary of graphs April 22, 2024Problem: Prove the sentence $\forall x \forall y(xEy \rightarrow \neg x=y)$ in the vocabulary of graphs using the axioms of graph theory. So far: The axioms of graph theory given are antireflexivity and symmetry. Here $xEy$ means there's an edge between the vertices $x$ and $y$. We were told we'd need identity axioms for this […]categoricallystupid
Recent Comments