The following are the scores of 20 students at New York City College of Technology; 222, 233, 241, 251, 268, 276, 220, 238, 253, 249, 236, 247, 256, 261, 227, 257, 244, 239, 242
A. Construct a frequency distribution using 6 classes.
Subtract the highest value (276) by the lowest value (220) to get 56. Divide 56 by the number of classes (6) to obtain 9.3. Round 9.3 down to 9.
Select the lower limit of the first class. The lowest limit to 220
Add the class width to the lower limit of the first class to calculate the upper limit of the first class and the lower limit of the next class. Continue until all classes are completed. Add 9 to 220 to get the first class (220-229) and continue as follows:
(220-229)
(230-239)
(240-249)
(250-259)
(260 – 269)
(270-279)
Determine the frequencies for each class by counting the number of data values that fit for each class. The total frequency value should be equal to the total number of data values. Given the student scores:
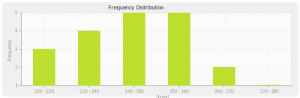
(220-229) 3
(230-239) 4
(240-249) 5
(250-259) 5
(260 – 269) 2
(270-279) 1
B. Draw a histogram for the frequency distribution in part (a)
* X-Axis is for the frequency distribution class, and the Y-Axis is for the amount in those classes.
C. Draw a frequency polygon for the frequency distribution in part a
A Frequency polygon uses dots to connect the data instead of a straight line or bars
* X-Axis is for the frequency distribution class, and the Y-Axis is for the amount in those classes.
Good Luck,
Glen.




Hey, i believe you did it wrong… when you find out class width- you have to round up the number (almost always) so class width here is 10 not 9