STUDY GUIDE FOR PROBLEM # 15
By Anthony Marc
15) It is claimed that the average annual per person spending on prescription drugs is $410. If a survey of 65 randomly selected people indicated an average spending of $425 with a standard deviation of $45, do we reject the claim that the average is $410? Use a 5% level of significance.
- The first thing to do is construct a hypothesis test with a null and alternative hypothesis to test whether the claim will be greater, less than or equal to the average of what is already stated. The tails of the test refer to the area in the normal curve which corresponds to the alternative hypothesis (the region where we you reject the null hypothesis). The claim states that the average per person annually spending on prescription drugs is $410.
- Ho (The null hypothesis) would be that the average spent would be equal to $410 and Ha (the alternative hypothesis) would also not be equal to $410. Both hypotheses are considered not equal due to the fact that average is NOT more or less than $410 but is exactly that number $410 being spent.
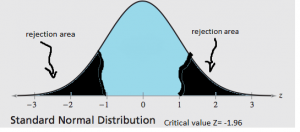
- It’s a two tailed test
- The level of significance is the amount on the normal curve whose maximum probability determines whether or not to reject the claim from the mean to the rejection area.
- The level of significance is 5% which comes out to 5/100= .0500. Since the normal distribution curve is two tailed the level of significance has to be divided by two to determine the rejection area.
- .0500/2= .0250 for both ends of the curve. Looking on the table the critical value comes out to z = -1.96.
SOLUTION:
- The problem would be done as: , Z= 425-410/45 and the square root of 65
- What made it easier for me to solve this problem was do it step by step starting off with the square root of n= 65, which comes out to 8.062257748.
- Then divide that sum by the standard deviation of 45, so you would divide 45/8.062257748 which comes to the answer of 5.581563057.
- Then subtract the average by the sample mean (425-410) and divide (5.581563057) which come to the answer of Z= 2.687419249.
- So as a result we REJECT the claim.
The claim is rejected due to the fact that the Z score is higher than the critical value which determines whether or not it falls within the range of values whether the claim is acceptable. So people annually spend more than the average $410 per year on prescription drugs.