42. Suppose that f (x) is O(g(x)). Does it follow that 2^f (x) is O(2^g(x))?
f (x) is O(g(x)) or f(x) ≤ g(x)
Then 2^ f(x) ≤ 2^g(x)
Therefore, 2^f(x) is O(2^g(x))
42. Suppose that f (x) is O(g(x)). Does it follow that 2^f (x) is O(2^g(x))?
f (x) is O(g(x)) or f(x) ≤ g(x)
Then 2^ f(x) ≤ 2^g(x)
Therefore, 2^f(x) is O(2^g(x))
Our goal is to make the OpenLab accessible for all users.
Our goal is to make the OpenLab accessible for all users.

Corrections at :
http://rpubs.com/thebunnyknight/158590
I agree but x^2 is not an exponential function. It is a power function…I am sure that’s what you meant.
This is kind of a tricky question, huh? Andy, Eric is absolutely right. It looks like in your proof you’re assuming that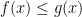 , but this doesn’t have to be true. The statement that
, but this doesn’t have to be true. The statement that  is
is  is strictly weaker, so you can’t use the simple inequality the way that you want to.
is strictly weaker, so you can’t use the simple inequality the way that you want to.
Eric’s link contains a nice example of functions and
and 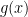 such that
such that  is
is  but
but 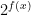 is not
is not 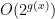 .
.