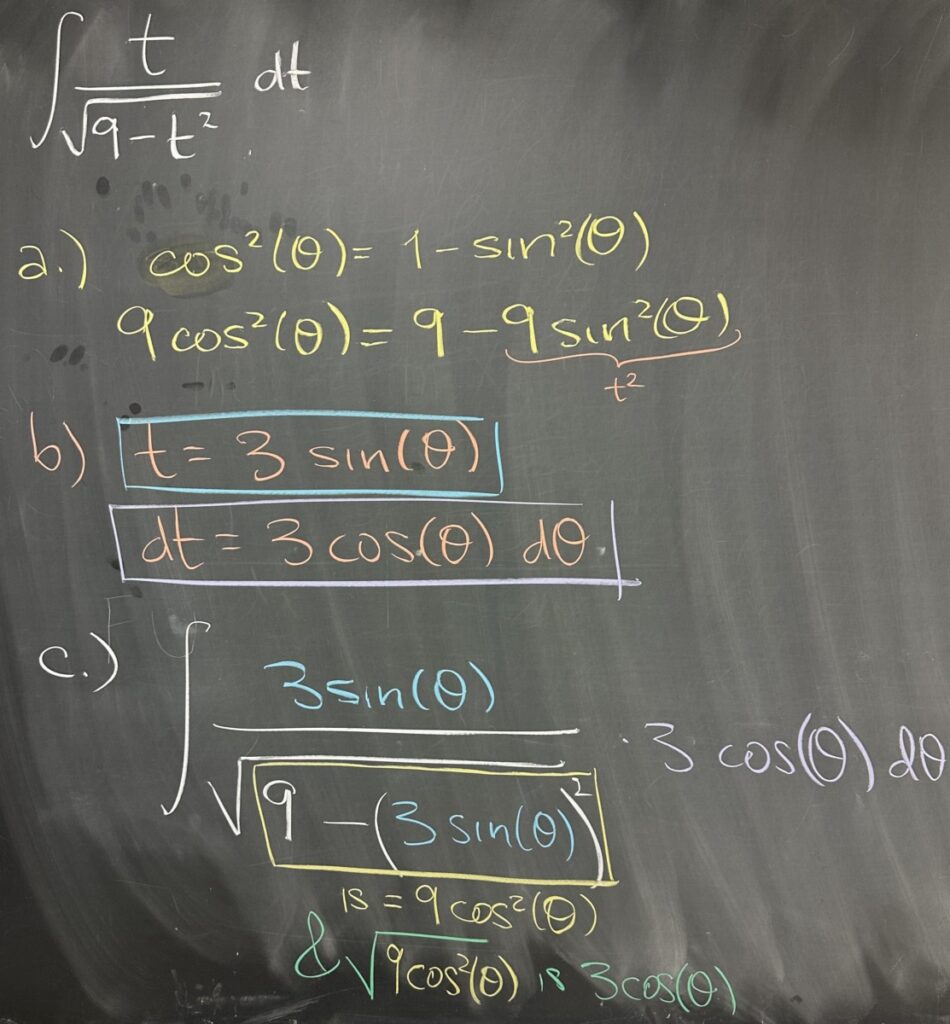
Today’s quiz focused on the steps necessary for the use of ‘trig substitution’ to find the antiderivative \(\int\frac{t}{\sqrt{9-t^2}}\,dt\). Our first task is to identify the relevant pythagorean identity for simplifying the given function. In this case, we see a radicand of \(9-t^2\) which indicates that we will want to use the identity: \(1-\sin^2(\theta)=\cos^2(\theta)\), and more specifically (after multiplying all terms by \(9\)): \(9-9\sin^2(\theta)=9\cos^2(\theta)\).
Since our integral has \(9-t^2\), and we want to use the pythagorean identity on \(9-9\sin^2(\theta)\), our next step is to choose the substitution \(t=3\sin(\theta)\). This choice ensures that we end up with the desired pythagorean identity, but we must remember that we are not just substituting \(t\), but the differential \(dt\) as well. Since we chose \(t=3\sin(\theta)\), the differential is \(dt=3\cos(\theta)\,d\theta\).
Here we want to point out that \(\sqrt{9-t^2}\) becomes \(\sqrt{9-9\sin^2(\theta)}\), then the pythagorean identity makes this \(\sqrt{9\cos^2(\theta)}\), which simplifies to \(3\cos(\theta)\). This all takes place in the denominator of our original integral:
\[\int\frac{t}{\textcolor{blue}{\sqrt{9-t^2}}}\textcolor{purple}{\,dt}=\int\frac{3\sin(\theta)}{\textcolor{blue}{3\cos(\theta)}}\cdot\textcolor{purple}{3\cos(\theta)\,d\theta}\]
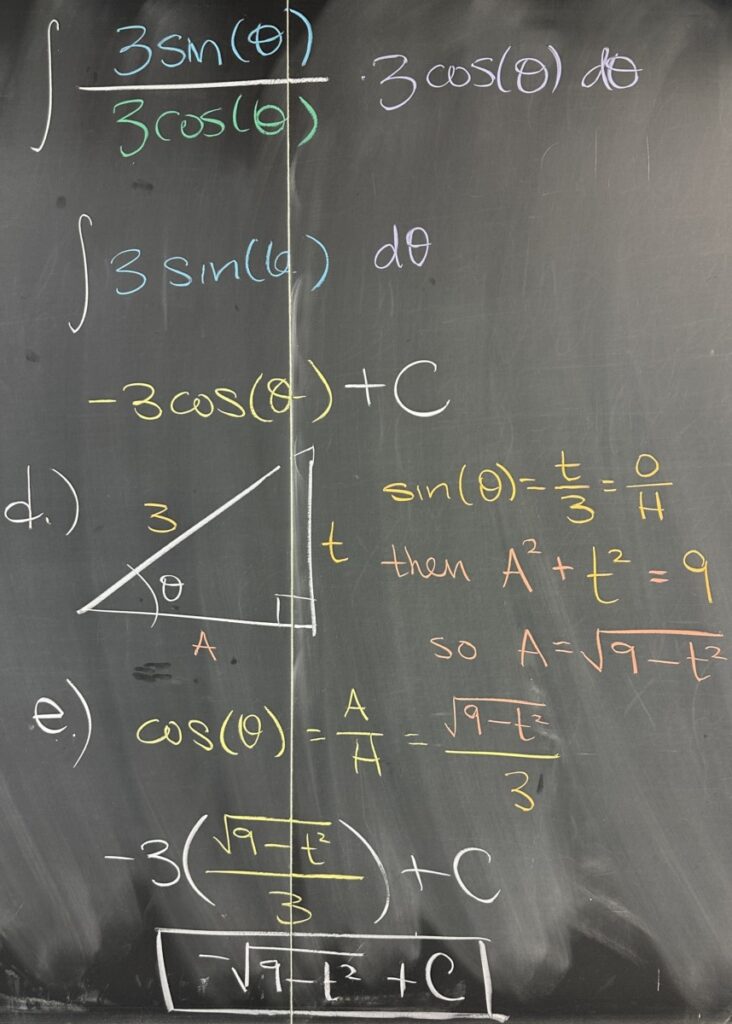
We then see that the factors of \(3\cos(\theta)\) reduce, leaving us with \[\int\frac{3\sin(\theta)}{3\cos(\theta)}\cdot 3\cos(\theta)\,d\theta = \int 3\sin(\theta)\,d\theta=-3\cos(\theta)+C\]
We’ve found our antiderivative, now all that is left is to convert our result from being a function of \(\theta\) back to being a function of our original variable, \(t\).
We substituted \(t=3\sin(\theta)\), which is equivalent to saying \(\frac{t}{3}=\sin(\theta)\). Since we have an expression for sine of \(\theta\), but we want an expression for cosine of \(\theta\), we consider a right triangle with angle \(\theta\). Since the sine ratio for \(\theta\) is \(\frac{t}{3}\), the opposite leg has length \(t\), and the hypotenuse has length \(3\). We want to determine an expression for the cosine ratio (adjacent divided by hypotenuse), which means we must find the length of the adjacent leg. Using the pythagorean theorem, we know that the adjacent leg has length \(\sqrt{9-t^2}\).
Finally, we can say that \[-3\cos(\theta)+C=-3\left(\frac{\sqrt{9-t^2}}{3}\right)+C=-\sqrt{9-t^2}+C\]
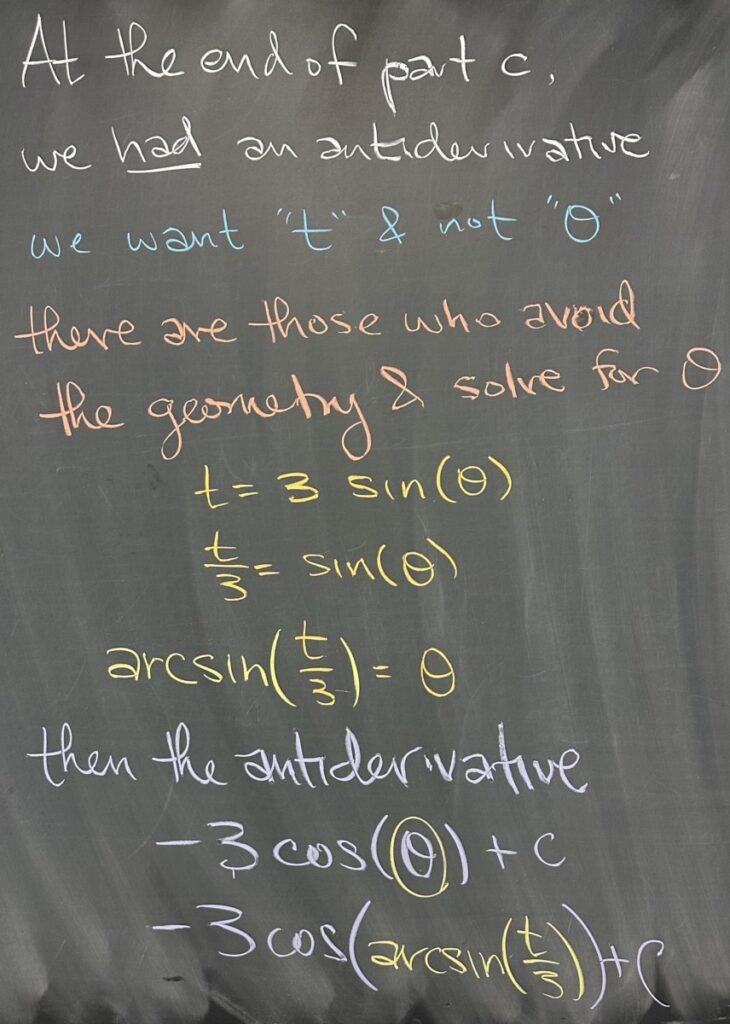
It is important to note that there are multiple ways to approach the task of taking our antiderivative in terms of \(\theta\)(\(-3\cos(\theta)+C\)) and converting it into a function of \(t\).
Instead of drawing out a right triangle and using trig ratios, one might instead solve for \(\theta\) directly: \[\sin(\theta)=\frac{t}{3}\quad\longrightarrow\quad\theta=\arcsin\left(\frac{t}{3}\right)\]
Since we have an exact expression for \(\theta\), it can be directly substituted into our result: \[-3\cos(\textcolor{purple}{\theta})+C=-3\cos\left(\textcolor{purple}{\arcsin\left(\frac{t}{3}\right)}\right)+C\]
This result is a function of \(t\), but it is much harder to interpret compared to the (equivalent) version that we got from the trig ratio approach: \(-\sqrt{9-t^2}+C\).
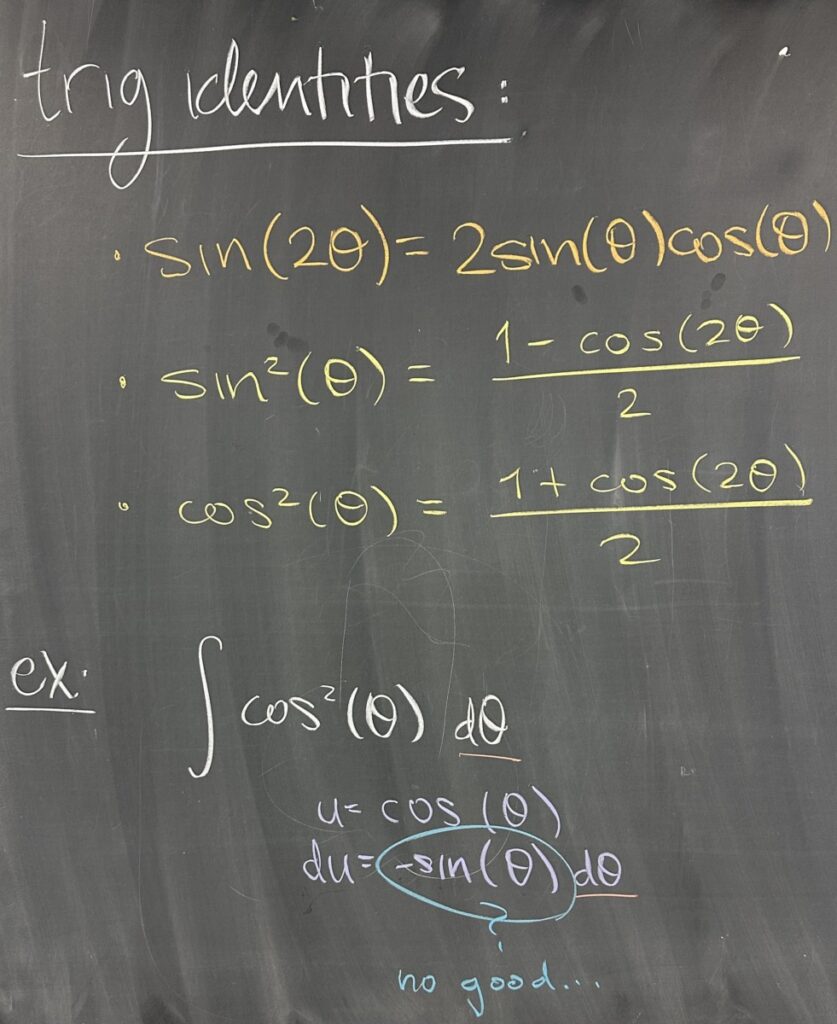
Often, when applying the method of trig substitution, our integrals will end up similar to our “trig integrals“. We handled most of those problems (again) through the use of pythagorean trig identities. However, sometimes, other trig identities might be necessary. Three important identities to be aware of:
- \(\sin(2\theta)=2\sin(\theta)\cos(\theta)\)
- \(\sin^2(\theta)=\frac{1-\cos(2\theta)}{2}\)
- \(\cos^2(\theta)=\frac{1+\cos(2\theta)}{2}\)
Next, we work through an example that uses one of these identities: \(\int\cos^2(\theta)\,d\theta\). Note here that \(\cos^2(\theta)\) is a composition of functions, with the ‘inner’ function being \(\cos(\theta)\). Typically, we would think of trying to substitute \(u=\cos(\theta)\)… but in that case we would also be required to substitute \(du=-\sin(\theta)\,d\theta\) — and we simply do not have any factors of \(\sin(\theta)\) to substitute to get \(du\).
In class, we also discussed the possibility of swapping \(\cos^2(\theta)\) for \(1-\sin^2(\theta)\), but then we end up with the same type of situation where our desired substitution has a differential that we lack the factors to accommodate.
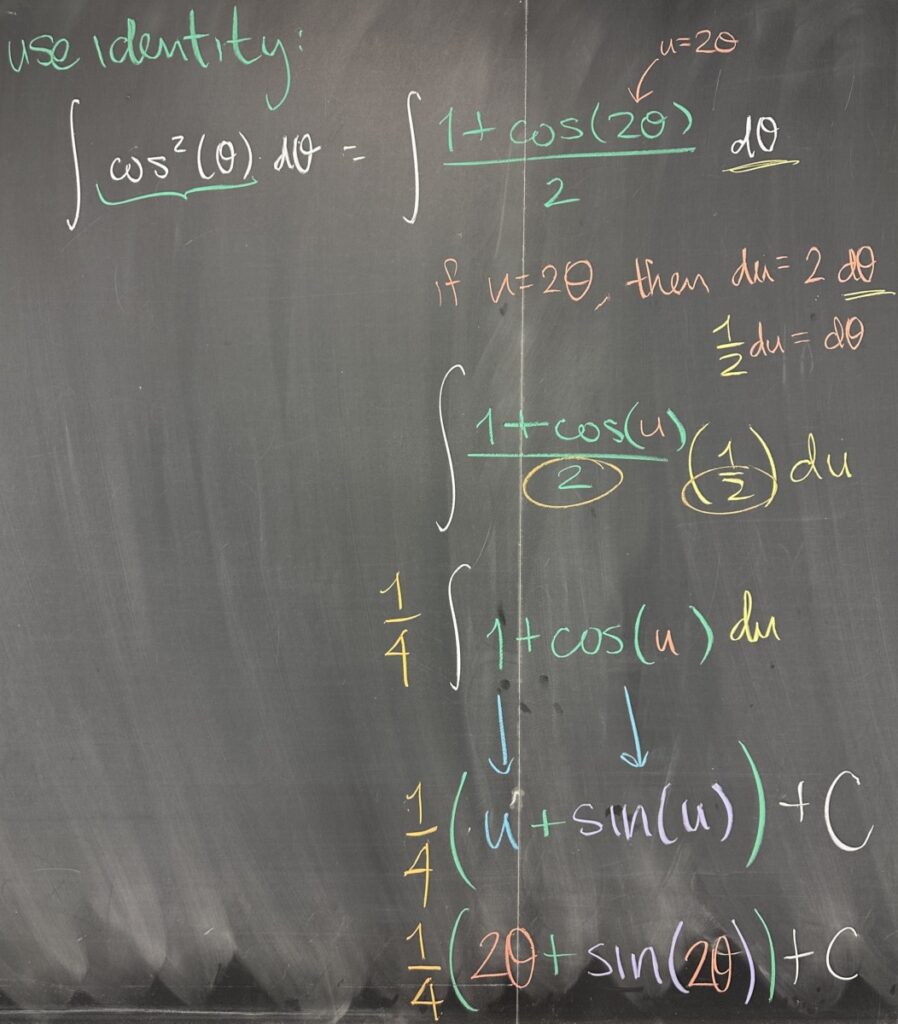
Instead we use the identity \(\cos^2(\theta)=\frac{1+\cos(2\theta)}{2}\): \[\int\cos^2(\theta)\,d\theta=\int\frac{1+\cos(2\theta)}{2}\,d\theta\]
Now, instead, our composition of functions (\cos(2\theta)\) has ‘inner’ function \(u=2\theta\), which has a differential that we can accommodate: \(du=2\,d\theta\). It’s alright that we don’t have a factor of \(2\) (since it’s constant), we can instead substitute the differential as \(\frac12\,du=d\theta\): \[\int\frac{1+\cos(2\theta)}{2}\,d\theta=\int\frac{1+\cos(u)}{2}\left(\frac12\right)\,du\]
\[\int\frac{1+\cos(u)}{2}\left(\frac12\right)\,du=\frac14\int 1+\cos(u)\,du\]
\[\frac14\int 1+\cos(u)\,du=\frac14\left(u+\sin(u)\right)+C\]
Substituting \(2\theta\) back in for \(u\), we end up with a final result: \[\int\cos^2(\theta)\,d\theta=\frac14(2\theta+\sin(2\theta))+C\]
[Keep this in mind, we’ll use this result later]
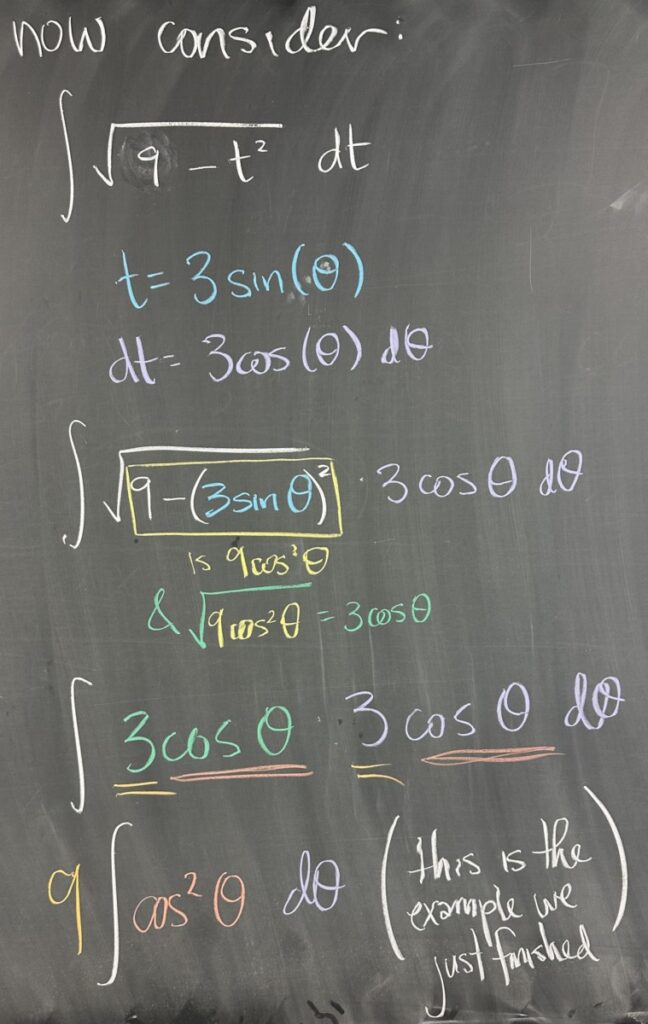
Now we consider a trig substitution problem, \(\int\sqrt{9-t^2}\,dt\). Similar to the quiz problem earlier, we recognize the desired trig identity: \(9-9\sin^2(\theta)=9\cos^2(\theta)\) and make the corresponding substitution: \(t=3\sin(\theta)\) and differential: \(dt=3\cos(\theta)\,d\theta\).
Again, similar to the earlier quiz problem, the radical \(\sqrt{9-t^2}\) simplifies to \(3\cos(\theta)\) and we end up with the trig substitution: \[\int\textcolor{blue}{\sqrt{9-t^2}}\,\textcolor{purple}{dt}=\int\textcolor{blue}{3\cos(\theta)}\textcolor{purple}{3\cos(\theta)\,d\theta}\]
So now we are left to integrate \(9\int\cos^2(\theta)\,d\theta\), which happens to be \(9\) times the integral that we just completed!
For a moment, consider what would be necessary if we hadn’t already completed the integral \(\int\cos^2(\theta)\,d\theta\). At this point, it is recommended that you complete complicated trig integrals separately from the trig substitution steps. This can help to avoid confusion, and also help in remembering that simply completing the trig integral is not enough — we must finish by unraveling the trig substitution.
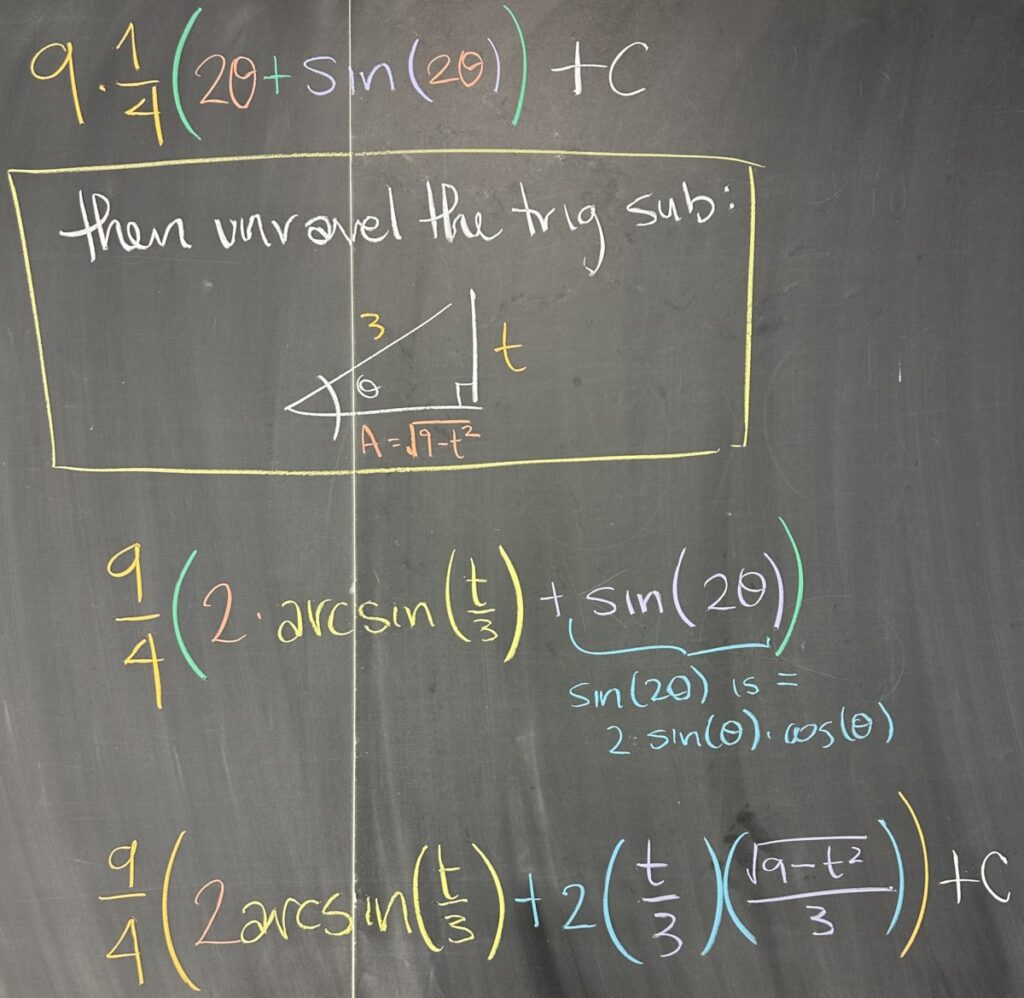
So far, we have found: \[\int\sqrt{9-t^2}\,dt=9\int\cos^2(\theta)\,d\theta=\frac94\left(2\theta+\sin(2\theta)\right)+C\]
And now we must unravel the trig substitution (convert our function of \(\theta\) back to a function of \(t\)). Since we used the same substitution as the earlier quiz problem, the right triangle for \(\theta\) would be the same: the opposite leg has length \(t\), the hypotenuse has length \(3\), and the adjacent leg has length \(\sqrt{9-t^2}\). We also know that directly solving for \(\theta\), we get \(\theta=\arcsin\left(\frac{t}{3}\right)\).
However, we have an issue with the fact that we must convert \(\sin(2\theta)\), but we can only find trig ratios for \(\theta\) (not \(2\theta\)). Here, we use another of the recommended trig identities: \(\sin(2\theta)=2\sin(\theta)\cos(\theta)\), so now we have trig ratios for \(\theta\).
\[\frac94\left(2\theta+\textcolor{darkgreen}{\sin(2\theta)}\right)+C=\frac94\left(2\theta+\textcolor{darkgreen}{2\sin(\theta)\cos(\theta)}\right)+C\]
From our right triangle, we know that \(\sin(\theta)=\frac{t}{3}\) and \(\cos(\theta)=\frac{\sqrt{9-t^2}}{3}\). Since we also have \(\theta\) without a trig ratio in our result, we also need \(\theta=\arcsin\left(\frac{t}{3}\right)\).
\[\frac94\left(2\theta+2\sin(\theta)\cos(\theta)\right)+C=\frac94\left(2\arcsin\left(\frac{t}{3}\right)+2\left(\frac{t}{3}\right)\left(\frac{\sqrt{9-t^2}}{3}\right)\right)+C\]

Finally, we look at another trig substitution example, but this time, one that does not use the same pythagorean trig identity. \(\int\frac{\sqrt{x^2-9}}{x^3}\,dx\) differs slightly from our earlier examples, in that we have \(x^2-9\) (subtracting a constant) instead of \(9-t^2\) (where we subtract from a constant). The corresponding pythagorean identity for this situation is \(\sec^2(\theta)-1=\tan^2(\theta)\), or in this case: \(9\sec^2(\theta)-9=9\tan^2(\theta)\).
In order to use this substitution, we would need to substitute \(x\) in such a way that \(x^2\) is replaced by \(9sec^2(\theta)\). That means choosing \(x=3\sec(\theta)\), and then the corresponding differential must be \(dx=3\sec(\theta)\tan(\theta)\,d\theta\).
Similar to previous examples, we choose our substitution specifically to reduce the square-root in our integral expression: \(\sqrt{x^2-9}\). Here, \(x^2-9\) becomes \(9\sec^2(\theta)-9\), which is equivalent to \(9\tan^2(\theta)\) and then has square-root: \(3\tan(\theta)\).
\[\int\frac{\textcolor{darkblue}{\sqrt{x^2-9}}}{x^3}\,\textcolor{purple}{dx}=\int\frac{\textcolor{darkblue}{3\tan(\theta)}}{27\sec^3(\theta)}\textcolor{purple}{3\sec(\theta)\tan(\theta)\,d\theta}\]
From here, we combine all of our numerical factors: \(\frac{3\cdot 3}{27}=\frac13\), factors of tangent: \(\tan(\theta)\cdot\tan(\theta)=\tan^2(\theta)\), and factors of secant: \(\frac{\sec(\theta)}{\sec^3(\theta)}=\frac{1}{\sec^2(\theta)}\), leaving us with the integral: \(\int\frac{\tan^2(\theta)}{\sec^2(\theta)}\,d\theta\).
The fraction of tangent and secant can be reduced as follows: \[\frac{\tan^2(\theta)}{\sec^2(\theta)}=\frac{\frac{\sin^2(\theta)}{\cos^2(\theta)}}{\frac{1}{\cos^2(\theta)}}=\frac{\sin^2(\theta)}{\cos^2(\theta)}\cdot\frac{\cos^2(\theta)}{1}=\sin^2(\theta)\]
So far, our trig substitution brings us to this point: \[\int\frac{\sqrt{x^2-9}}{x^3}\,dx=\frac13\int\sin^2(\theta)\,d\theta\]
At this point, you should turn to a new page in your notebook and workout the integral \(\int\sin^2(\theta)\,d\theta\). Then, return to this point and finish unraveling the trig substitution.




Recent Comments