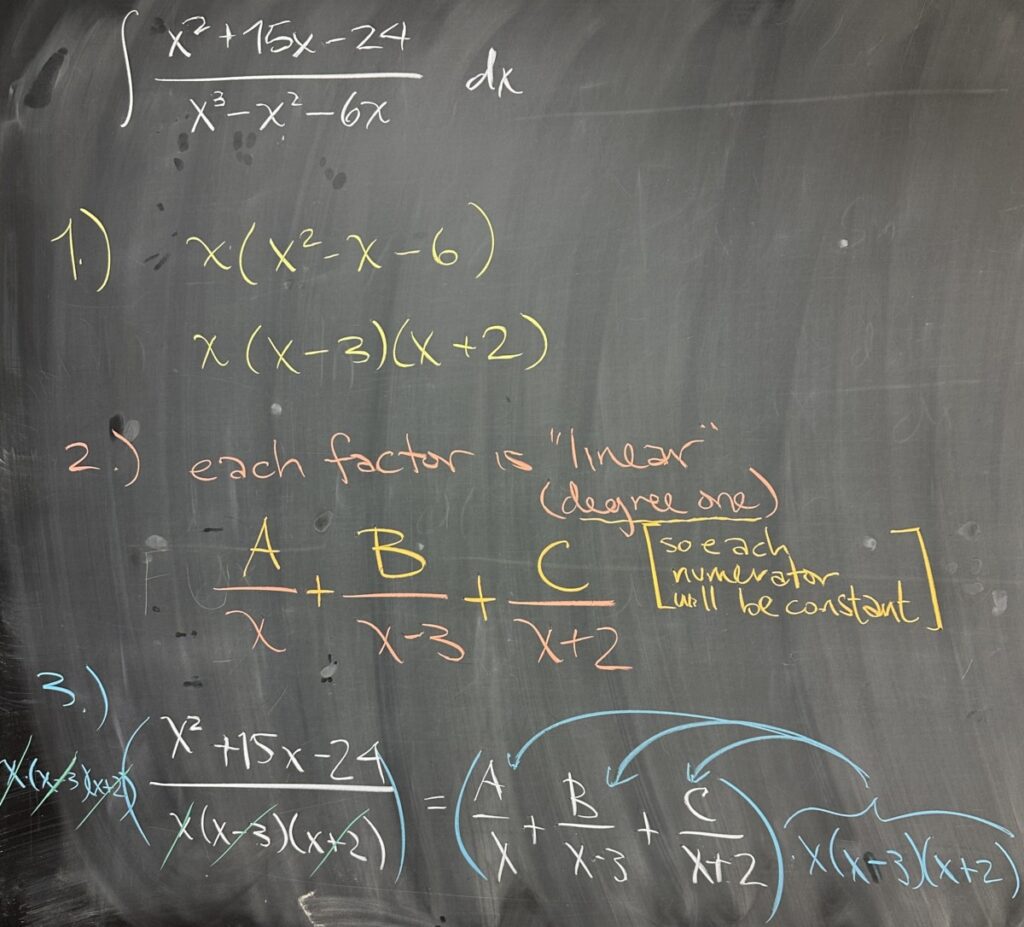
Today’s quiz walks through the steps necessary for Partial Fraction Decomposition. The first step is always identifying the factors in the denominator, and here we see: \(x^3-x^2-6x=x(x-3)(x+2)\).
Here, the factors that we found were all “linear” (meaning each has degree one as a polynomial), and so each “partial” fraction will be a constant numerator with a linear denominator: \(\frac{A}{x}+\frac{B}{x-3}+\frac{C}{x+2}\).
Since our goal is to have an equivalent representation of our original fraction, the decomposition must be equal to the fraction we started with: \[\frac{x^2+15x-24}{x(x-3)(x+2)}=\frac{A}{x}+\frac{B}{x-3}+\frac{C}{x+2}\]
Then our next steps focus on identifying the specific values for \(A\), \(B\), and \(C\) that will make our expressions equivalent. In order to solve for these unknown values, we multiply our equation through by the common denominator \(x(x-3)(x+2)\): \[x(x-3)(x+2)\left(\frac{x^2+15x-24}{x(x-3)(x+2)}\right)=\left(\frac{A}{x}+\frac{B}{x-3}+\frac{C}{x+2}\right)x(x-3)(x+2)\]
The left-hand side of this equation reduces in a straightforward manner, as all three factors reduce. On the right-hand side, the factors are distributed to all three fractions, and each fraction reduces the single factor in its denominator:\[x^2+15x-24=A(x-3)(x+2)+Bx(x+2)+Cx(x-3)\]
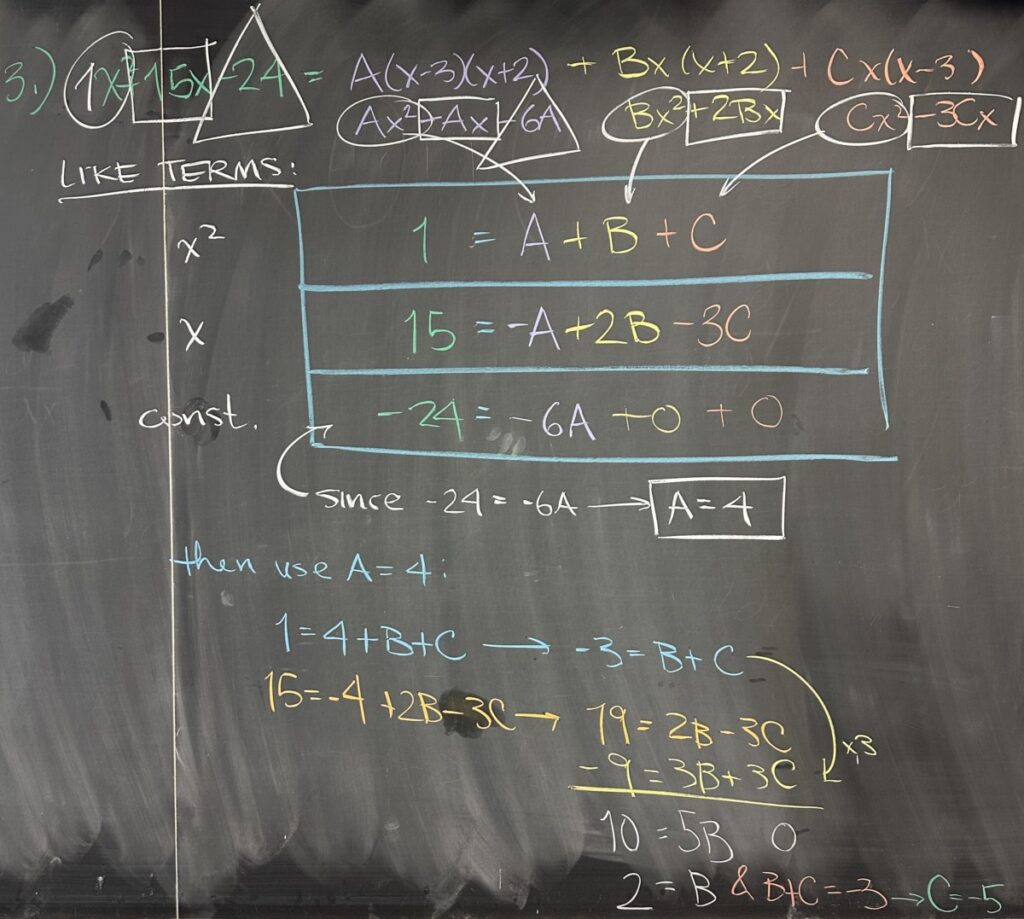
Although this only a single equation (and we’re trying to find three unknown values), we are actually able to derive three equations from it. Consider that only “like” terms may interact, so each of the three unlike terms must be equal on both sides of the equation: the quadratic terms, the linear terms, and the constant terms:
- quadratic: \(1x^2 = Ax^2+Bx^2+Cx^2\), so \(1=A+B+C\)
- linear: \(15x=-Ax+2Bx-3Cx\), so \(15=-A+2B-3C\)
- constant: \(-24=-6A+0B+0C\), so \(-24=-6A\)
That last equation, \(-24=-6A\), is only satisfied by \(A=4\). Then, using this information, the other two equations become:
- \(1=4+B+C\), so \(-3=B+C\)
- \(15=-4+2B-3C\), so \(19=2B-3C\)
We can use either substitution or elimination method on these two equations; but either way, we can conclude that \(B=2\) and \(C=-5\) form the only combination that satisfies both equations. So we end up with: \[\frac{x^2+15x-24}{x(x-3)(x+2)}=\frac{4}{x}+\frac{2}{x-3}+\frac{-5}{x+2}\]
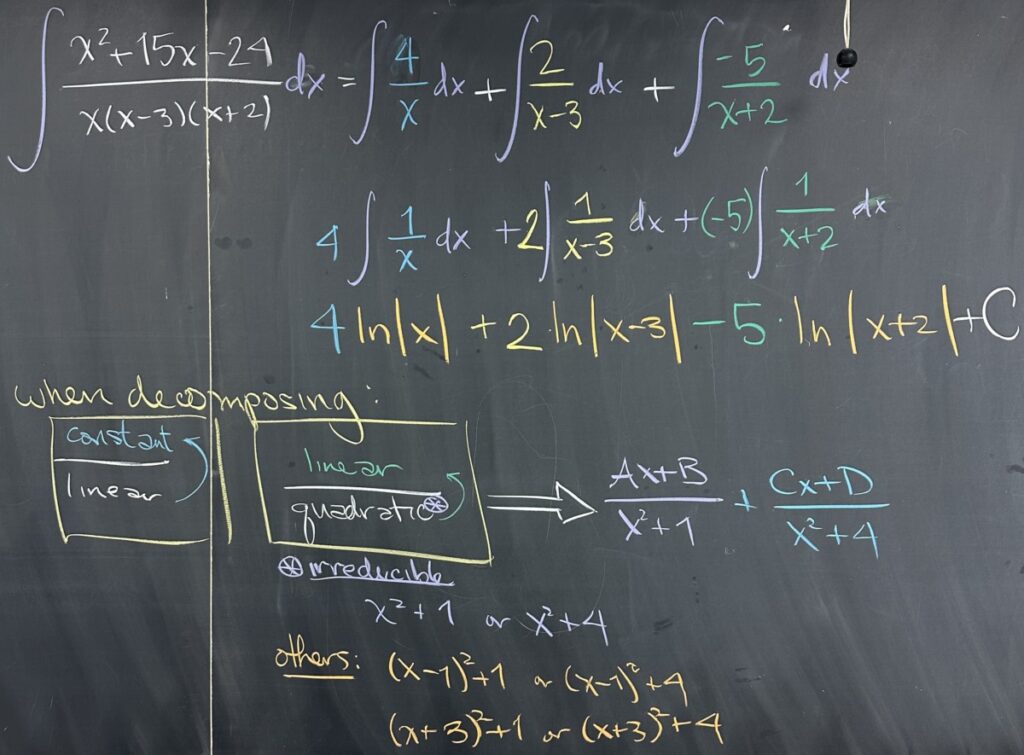
So our original integral can be found in three separate parts:
- \(\int\frac{4}{x}\,dx=4\ln|x|\)
- \(\int\frac{2}{x-3}\,dx=2\ln|x-3|\)
- \(\int\frac{-5}{x+2}\,dx=-5\ln|x+2|\)
Note that in each of the last two of these three integrals, a ‘free’ substitution can be made. A ‘free’ substitution is one in which the differentials for our original and substituted variables are equal. In the second integral, \(u=x-3\) has differential \(du=dx\). In the third, \(u=x+2\) has differential \(du=dx\). In each case, we are effectively integrating \(\frac{1}{u}\).
All together, our family of antiderivatives for the indefinite integral will be \[4\ln|x|+2\ln|x-3|-5\ln|x+2|+C\]
Note that we can find almost the entire result without finding the values of our unknown constants \(A\), \(B\), and \(C\). In class I explicitly discussed how anyone struggling to find the value of our unknown constants can still earn a good portion of the available credit on a problem by skipping straight through and finding the antiderivative without knowing the specific values of \(A\), \(B\), or \(C\).
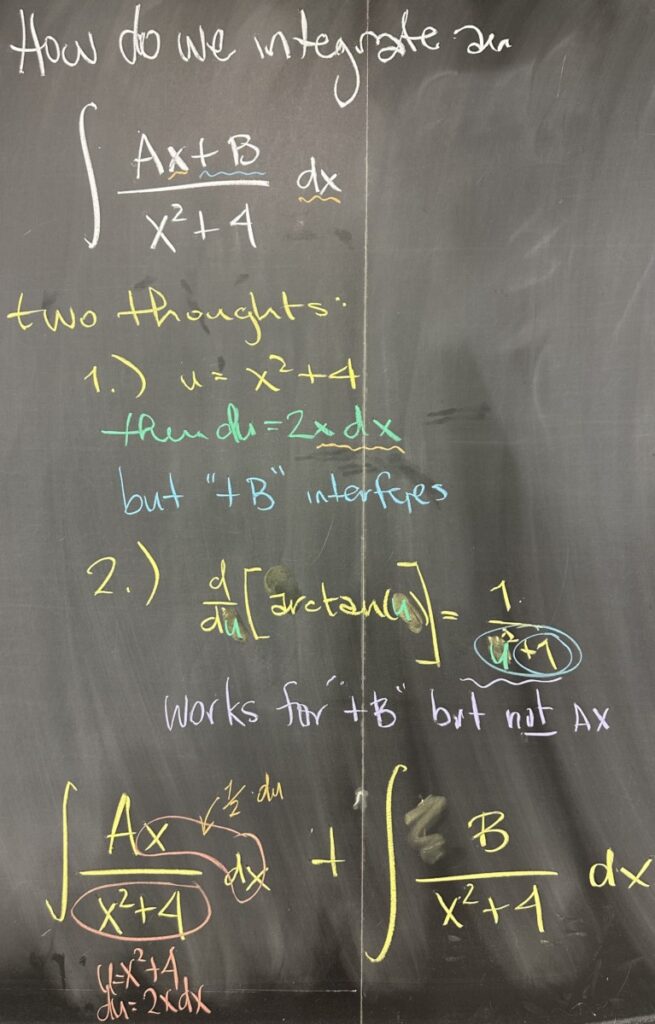
Next we look at what to do with irreducible quadratic denominators that may appear in partial fraction decomposition — such as \(\frac{Ax+B}{x^2+4}\).
Two approaches come to mind; first, substitution of the denominator, and second, the similarity with the derivative of \(\arctan(x)\).
In the first approach, substituting \(u=x^2+4\) would give us a differential \(du=2x\,dx\). This is ideal for a numerator like \(Ax\), but not when it includes \(+B\).
Alternatively, the form for \(\arctan(x)\) has a constant numerator, making it ideal for a numerator of \(B\), but not when it includes \(Ax\).
So what we will want to do is to separate the two terms of the numerator, creating separate fractions: \(\frac{Ax+B}{x^2+4}=\frac{Ax}{x^2+4}+\frac{B}{x^2+4}\).
In the first fraction, we will proceed with the u-substitution: \(u=x^2+4\) and \(du=2x\,dx\), giving us \[\frac{A}{2}\int\frac{1}{u}\,du=\frac{A}{2}\ln|x^2+4|\]
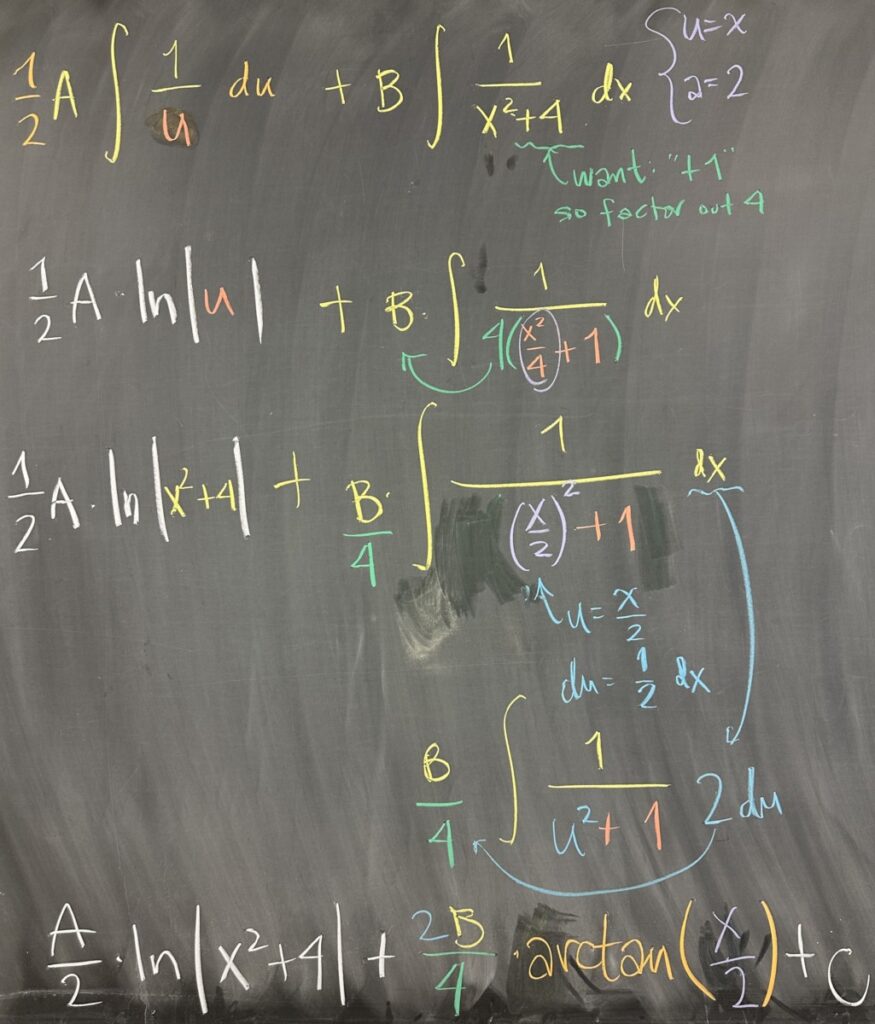
In the second term, we do some algebraic manipulation to see that \[\frac{B}{x^2+4}=\frac{B}{4(\frac{x^2}{4}+1)}=\frac{B}{4}\frac{1}{(\frac{x}{2})^2 + 1}\]
Here we can substitute \(u=\frac{x}{2}\) with differential \(du=\frac12\,dx\) and end up with \(\frac{B}{4}\int\frac{1}{u^2+1}2\,du=\frac{2B}{4}\arctan(\frac{x}{2})\)
All together, we end up with \[\int\frac{Ax+B}{x^2+4}\,dx=\frac{A}{2}\ln|x^2+4|+\frac{B}{2}\arctan\left(\frac{x}{2}\right)+C\]
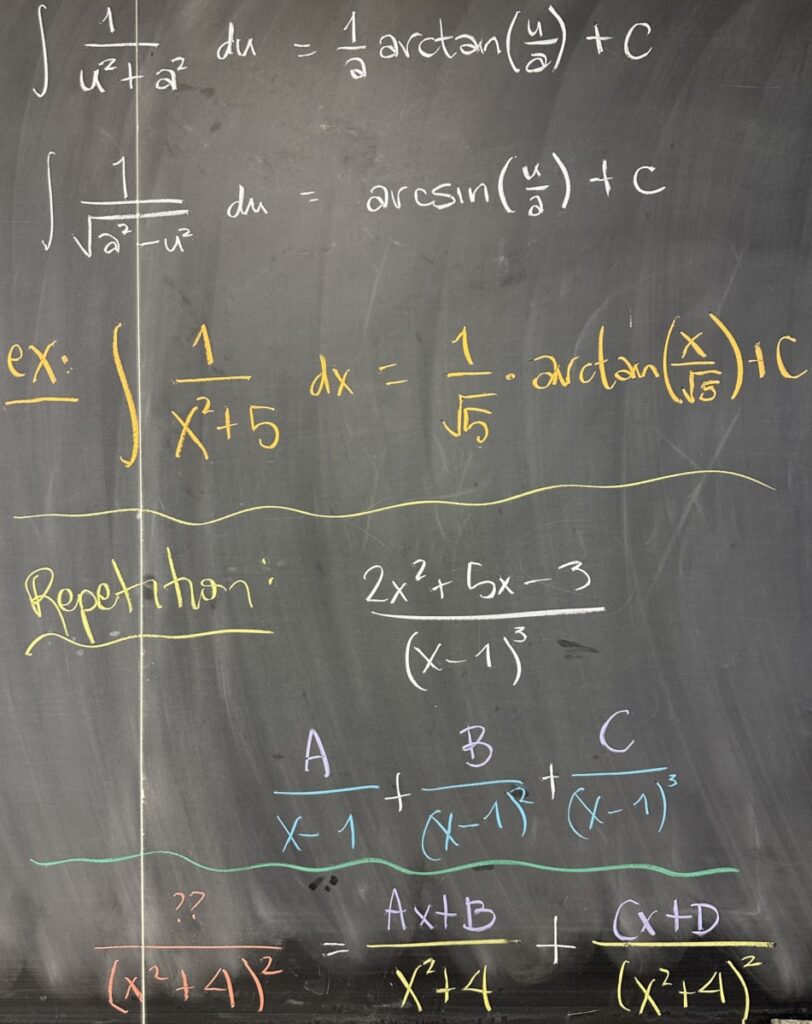
In general, we should note that any integral of the form \(\int\frac{1}{u^2+a^2}\,du=\frac{1}{a}\arctan\left(\frac{u}{a}\right)+C\). Knowing this general form will allow us to bypass a significant amount of algebraic manipulation as well as a u-substitution.
There are also times when we might see repeated factors in our denominator. When looking for the partial fraction decomposition of such fractions, it is essential that we consider all combinations of repeated factors.
For example, the decomposition of \(\frac{2x^2+5x-3}{(x-1)^3}\) must consider all possible reductions of the three repetitions of \(x-1\):\[\frac{A}{x-1}+\frac{B}{(x-1)^2}+\frac{C}{(x-1)^3}\]
The same holds for repeated irreducible quadratic factors: \[\frac{x^3-2}{(x^2+4)^2}=\frac{Ax+B}{x^2+4}+\frac{Cx+D}{(x^2+4)^2}\]

We spoke at the end of class about how the degrees of the numerator and denominator can impact the partial fraction decomposition.
First, we noticed that the number of unknown values (e.g. \(A\), \(B\), \(C\), and so on) is determined by the degree of the denominator. Each linear factor (degree one) will have one unknown (constant only) in the numerator; while each quadratic factor (degree two) will have two unknowns (linear term and constant) in the numerator.
Second, we noticed that our solution process required alignment of the like terms on both sides of the equation resulting from setting the original fraction equal to the sum of the decomposed fractions. These like terms always stopped one short of the degree in the denominator.
This observation tells us that partial fraction decomposition is only possible when the numerator has smaller degree than the denominator. (We can think of this being a ‘proper’ fraction of polynomials.)
When the degree of the numerator is larger (or equal to) the degree of the denominator, then we can actually perform the division indicated by the fraction to get a quotient (likely with some remainder). The remainder from such a division must have lower degree than the denominator.
Think of how this works with numbers. \(\frac{13}{5}\) is an improper fraction, as \(13\) can be divided by \(5\). The quotient is \(2\) and the remainder is \(3\), meaning that we can write \(\frac{13}{5}=2+\frac{3}{5}\).
In terms of polynomials, a fraction like \(\frac{x^2}{x^2+4}\) is considered ‘improper’, as the numerator does not have smaller degree. We can perform the division, as \(x^2+4\) would divide \(x^2\) with a quotient of \(1\) and a remainder of \(-4\).
One way to see this is: \[\frac{x^2}{x^2+4}=\frac{x^2+4-4}{x^2+4}=\frac{x^2+4}{x^2+4}+\frac{-4}{x^2+4}=1+\frac{-4}{x^2+4}\]
As you can see, the resulting remainder is a proper fraction.




Recent Comments