
Today’s first quiz problem is the indefinite integral \(\int t\cos(\pi t)\,dt\). Part a explicitly gave \(u=t\) and \(dv=\cos(\pi t)\,dt\), asking for \(du\) and \(v\) — both of which are necessary for the application of Integration by Parts.
Starting with \(du\), which is the derivative of \(u\), we see that \(du=1\,dt\). Finding \(v\) from \(dv\) is a little trickier, as \(v\) is the anti-derivative of \(dv\). So \(v=\int\cos(\pi t)\,dt\), which requires a substitution to complete.
Finding the antiderivative of \(\cos(w)\,dw\) would be nice, so we aim to substitute \(w=\pi t\). This gives us \(dw=\pi\,dt\), and since our integral does not contain a factor of \(\pi\) (and \(\pi\) is constant), we manipulate our differential to get \(dt=\frac{1}{\pi}\,dw\). With this substitution in hand, we now arrive at \[v=\frac{1}{\pi}\int\cos(w)\,dw=\frac{1}{\pi}\sin(w)=\frac1\pi\sin(\pi t)\]
After finding \(u,v,du,\text{ and }dv\), we’re ready to apply Integration by Parts \(\int u\,dv=uv-\int v\,du\): \[\int t\cos(\pi t)\,dt=\left(t\right)\left(\frac1\pi\sin(\pi t)\right)-\int\left(\frac1\pi\sin(\pi t)\right)\left(dt\right)\]
We can again use the substitution \(w=\pi t\) with the differential \(dt=\frac1\pi\,dw\), ending up with the final result: \[\frac1\pi t\sin(\pi t)-\frac1\pi\int \sin(w)\left(\frac1\pi\,dw\right)=\frac1\pi t\sin(\pi t)+\frac{1}{\pi^2}\cos(\pi t)+C\]

In the second problem, no guidance was provided on selecting \(u\) or \(dv\). Here, we are looking for the antiderivative of \(x^3\ln(x)\) — which is clearly a product of functions. How do we choose \(u\) and \(dv\)? Since the antiderivative of \(\ln(x)\) is quite complicated, it would be a poor choice as \(dv\) (since finding \(v\) would require the antiderivative). Therefore, we choose \(u=\ln(x)\), leaving \(dv=x^3\,dx\).
Then \(du=\frac{1}{x}\,dx\) and \(v=\int x^3\,dx=\frac14x^4\). Now that we know all four parts, we may apply Integration by Parts: \[\int x^3\ln(x)\,dx=\left(\frac14x^4\right)\left(\ln(x)\right)-\int\left(\frac14x^4\right)\left(\frac{1}{x}\,dx\right)\]
We can evaluate the remaining integral (combining \(\int x^4\cdot\frac{1}{x}=\int x^3\) and finding the antiderivative) to end up with the final result: \[\frac14x^4\ln(x)-\frac{1}{16}x^4+C\]

Moving on to today’s topic, we are going to need to first review the Pythagorean Trig Identities.
- \(\sin^2(x)+\cos^2(x)=1\), when translated into ratios of sides of a right triangle, shows why this identity is called “Pythagorean”
- \(\tan^2(x)+1=\sec^2(x)\) is the result of the previous identity divided by \(cos^2(x)\).
- \(1+\cot^2(x)=\csc^2(x)\) is the result of the first identity divided by \(\sin^2(x)\).

Next, we’ll need to review the derivatives of each of the trigonometric functions. This is because we’re going to do a lot of substitution — and whenever we want to substitute \(u\) for one of these trig functions, we’ll also have to attend to \(du\) (its derivative).
Note that for any of these derivatives besides sine and cosine, we can find the result by converting them into ratios of sine and cosine (and then apply chain rule or quotient rule, as needed).
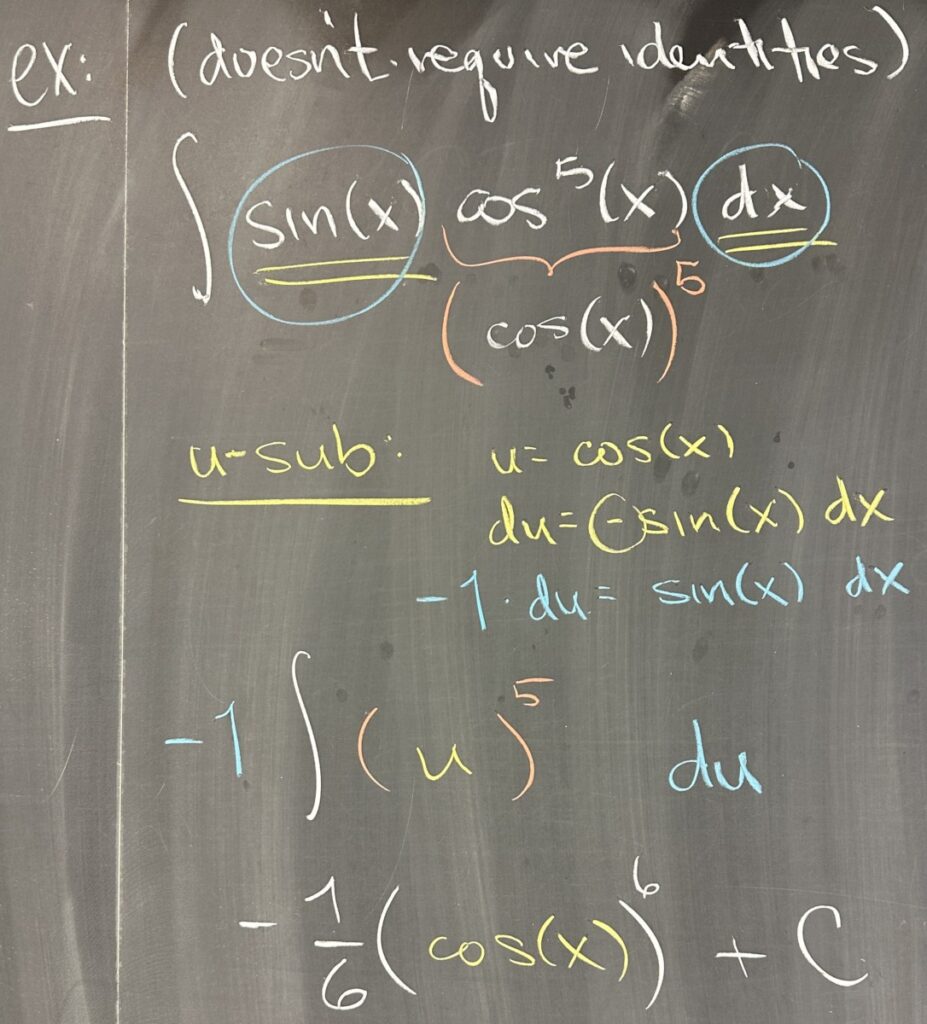
The first example does not use any of the trig identities that we just went over, but it does set the stage for what we want to do. Here we attempt to integrate \(\int\sin(x)\cos^5(x)\,dx\). We would like to substitute \(u=\cos(x)\), but can we also substitute the differential \(du=-\sin(x)\,dx\)?
Looking to the original integrand, we see that \(\sin(x)\,dx\) is present — so we manipulate the differential to see what we shoud replace it with: \(\sin(x)\,dx=-1\,du\).
After substituting both: \[\int\sin(x)\cos^5(x)\,dx=-\int u^5\,du=-\frac16 u^6+C=-\frac16\cos^6(x)+C\]

In the next example, we have “more copies” of sine: \(\int\sin^3(x)\cos^5(x)\,dx\)
The plan remains the same, with \(u=\cos(x)\) and \(-1\,du=\sin(x)\,dx\). The difference here is that we have \(\sin^3(x)\) in our integrand. We can split this into \(\sin^2(x)\sin(x)\), and use the single “copy” of sine (with \(dx\)) for substituting \(-1\,du\). The result is \[\int\sin^3(x)\cos^5(x)\,dx=\int\sin^2(x)u^5(-1\,du)\]
Now this is usually no good, since we cannot continue when we’ve got a mix of \(x\) and \(u\) (our substitution is ‘incomplete’ because we’ve still got some \(x\) hanging around). Is there any way for us to convert the remaining \(\sin^2(x)\) into some function of \(u\)?
This is where the Pythagorean Identities come into play. Since \(\sin^2(x)+\cos^2(x)=1\), we can conclude that \(\sin^2(x)=1-\cos^2(x)\). Moreover, since \(u=\cos(x)\), we can replace \(\sin^2(x)=1-u^2\): \[-\int(1-u^2)u^5\,du=-\int(u^5-u^7)\,du\]
We distributed \(u^5\) here because we cannot integrate products, but the distributed form is the difference of functions that we can integrate separately.

Using the power rule on both \(u^5\) and \(u^7\), we end up with \[-\int(u^5-u^7)\,du=-\left(\frac16u^6-\frac18u^8\right)+C=-\frac16\cos^6(x)+\frac18\cos^8(x)+C\]
What if we had tried this same integral with a different approach? What if we tried using \(u=\sin(x)\) instead? Then \(du=\cos(x)\,dx\), and we would need to separate off a copy of cosine (as we did with sine before): \(\cos^5(x)=\cos^4(x)\cos(x)\). Then \[\int\sin^3(x)\cos^4(x)\cos(x)\,dx=\int u^3\cos^4(x)\,du\]
Again, we end up with a mix of \(x\) and \(u\), so we cannot proceed. This time, we need to convert \(\cos^4(x)\) into a function of \(u\). It might seem much different because we have four copies of cosine (instead of just two), but we can further split: \(cos^4(x)=\cos^2(x)\cos^2(x)\), and we can again use the Pythagorean Identity to replace \(\cos^2(x)=1-\sin^2(x)=1-u^2\).

As a result, we now have \[\int u^3\cos^2(x)\cos^2(x)\,dx=\int u^3(1-u^2)(1-u^2)\,du\]
As before, we cannot integrate products, but here we can use our algebra skills to find the result of this product: \[u^3(1-u^2)(1-u^2)=u^3(1-2u^2+u^4)=u^3-2u^5+u^7\]
Each of these powers of \(u\) can be integrated separately (they are added/subtracted, not multiplied), giving us a final result: \[\frac14\sin^4(x)-\frac13\sin^6(x)+\frac18\sin^8(x)+C\]
At this point we should have a BIG question — we did the problem two different ways, but shouldn’t we get the same answer each time? WHY did we end up with two seemingly different antiderivatives? Which one is “right”?
We then graphed both results:
What we see is two different functions from the same family of antiderivatives. They have a constant distance between them at every \(x\)-value. Another way to think of it is that both functions have the same tangent slope at every \(x\)-value — meaning that their derivatives are equal. This is the same as saying both functions are antiderivatives of the same function.
When we consider \(+C\) (including the whole family of antiderivatives) with both functions, it’s (hopefully) clear that both end up describing the same family.




Recent Comments