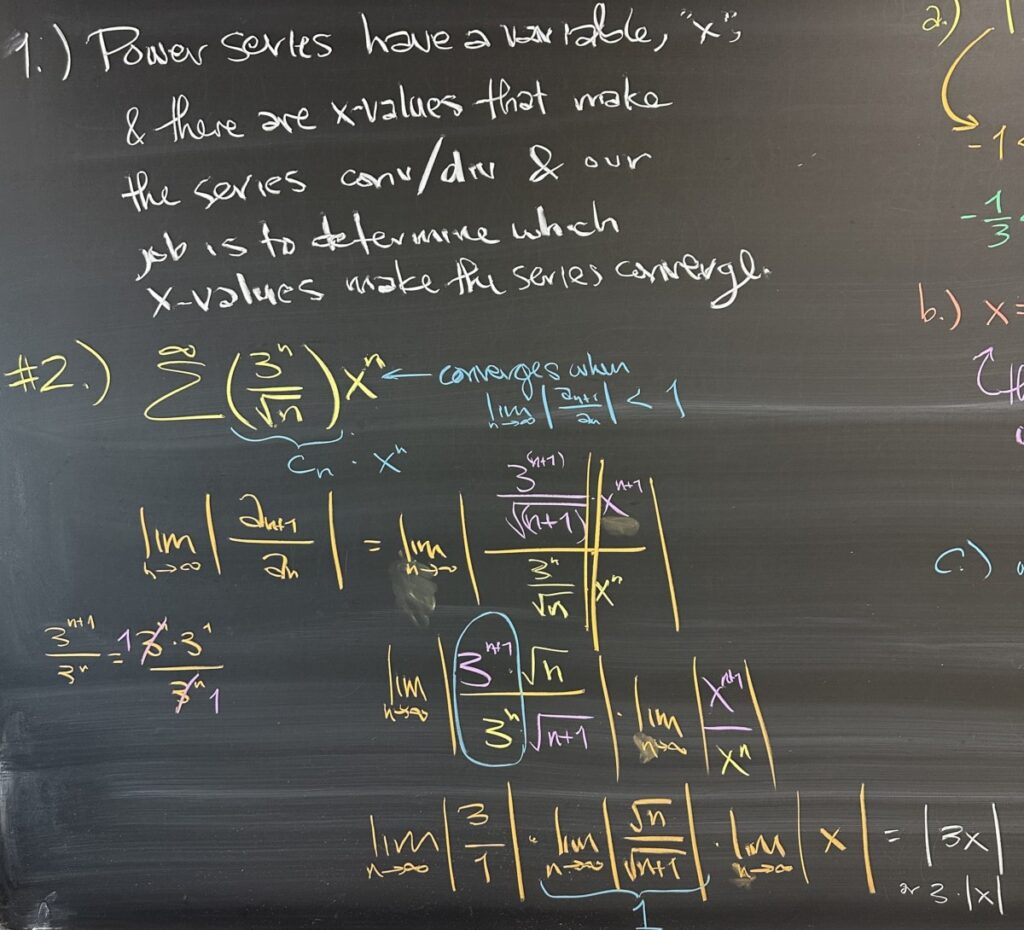
After today’s quiz, we started by talking about what makes “power series” different from the series that we’ve been working with so far this semester. The presence of
\(x\) as a variable in the series means that we have a series that can both converge AND diverge — depending on the value of \(x\).
When working with power series, the question is always: “what values of \(x\) will cause this series to converge?” And in order to answer this question, we always turn to the Ratio Test! This is because \(x^n\) is a geometric factor, and the presence of geometric factors always pushes us to use the Ratio Test.
We spent a fair amount of time deciding how to reduce the ratio — there is more than one way to handle it — but we do what we usually do, and try to line up similar factors. Every geometric factor will reduce (in the Ratio Test), and p-series factors will not reduce (although their limits are 1!). At the end of our limit computation, we found that \(\displaystyle\lim_{n\to\infty} \left|\frac{a_{n+1}}{a_n}\right| = 3|x|\).
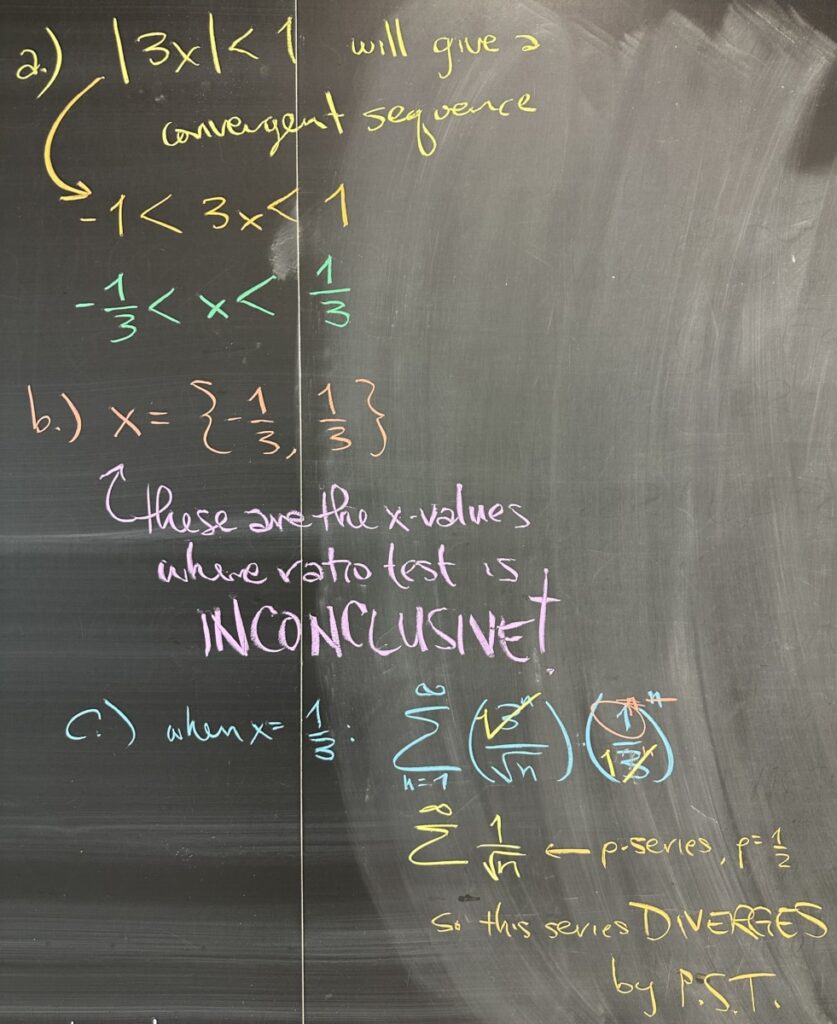
Our next task is to explicitly identify the \(x\)-values that cause our limit to be less than one. (Remember that the ratio test ensures that our series converges any time our limit is less than one.) That means unwrapping the absolute value inequality: \[3|x| < 1 \rightarrow |x| < \frac{1}{3} \rightarrow -\frac{1}{3} < x < \frac{1}{3}\]
Our endpoints are \(x = -\frac{1}{3}\) and \(x = \frac{1}{3}\). These \(x\)-values are important because they represent values where the Ratio Test is inconclusive. Because of this, we will need other tests to help us determine the convergence of the power series when \(x\) is either \(-\frac{1}{3}\) or \(\frac{1}{3}\).
We have to look at each endpoint separately. When \(x = \frac{1}{3}\), the series reduces to just \(\displaystyle\sum^\infty \frac{1}{\sqrt{n}}\). We should immediately recognize from the reduced form that this is a p-series (with \(p = \frac{1}{2}\)); and we know it will diverge by p-series Test (since \(p \leq 1\)).
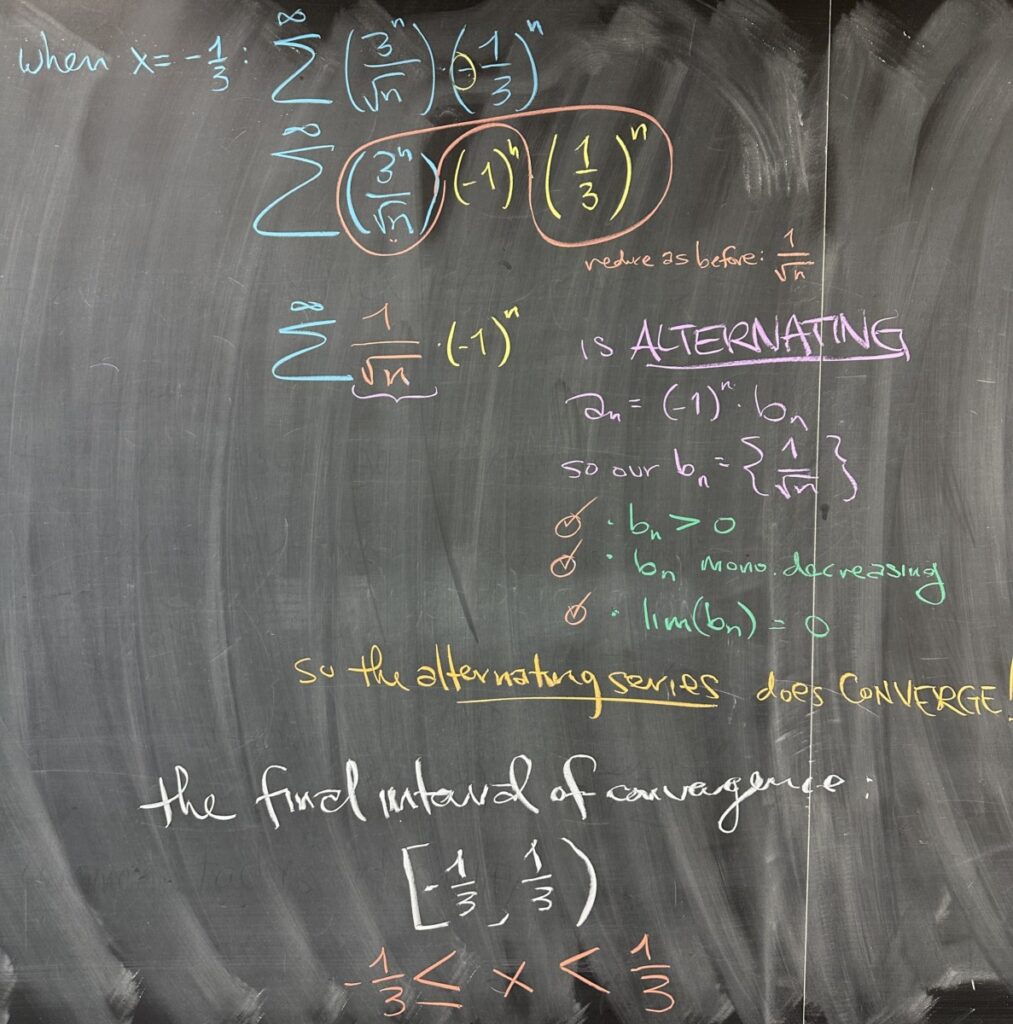
Then we check the other endpoint, \(x = -\frac{1}{3}\). When we replace \(x\) in the power series, our simplification is nearly identical except for the sign-alternation that happens because the base of our geometric term is negative (\(3^n\left(-\frac{1}{3}\right)^n = \left(-\frac{3}{3}\right)^n = (-1)^n\)). We should recognize this as an alternating series — so check the three requirements for convergence with the Alternating Series Test. We do that, and find that \(x = -\frac{1}{3}\) causes the power series to converge.
Putting all of our results together, we come to a final answer regarding the interval of convergence for the original power series. Our final interval of convergence includes \(x = -\frac{1}{3}\), but not \(x = \frac{1}{3}\). Written in interval notation, our final answer for the interval of convergence is \(\left[-\frac{1}{3}, \frac{1}{3}\right)\)
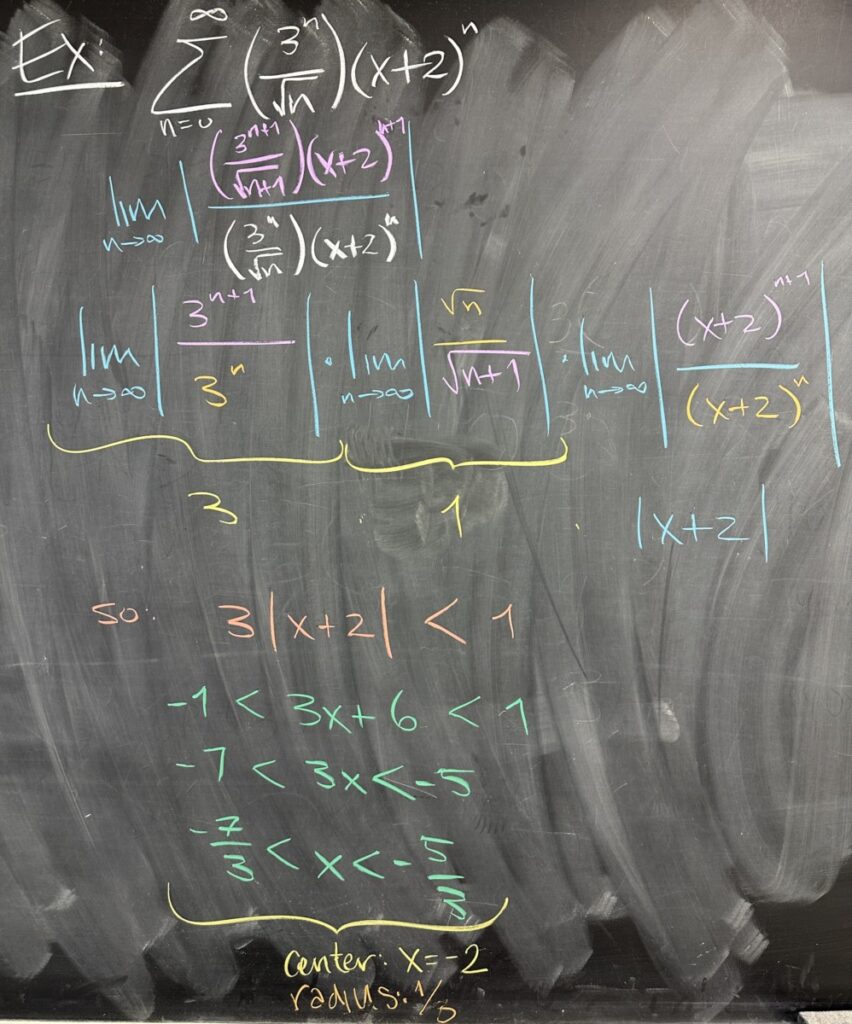
We turn to another example, which is just a slight modification to the previous power series. Instead of having \(x^n\), we have \((x+2)^n\), but this difference does not change our strategy. We still need to use the Ratio Test, and the ratio reduces in almost the exact same way.
What we find is that the interval of convergence is the same as the previous power series, only shifted (on the number line) two units to the left.
We also identified the “center” of the interval, and the “radius” (distance from center to endpoint). The center of our interval should be the \(x\)-value that causes our series to be \(\displaystyle\sum^\infty 0).
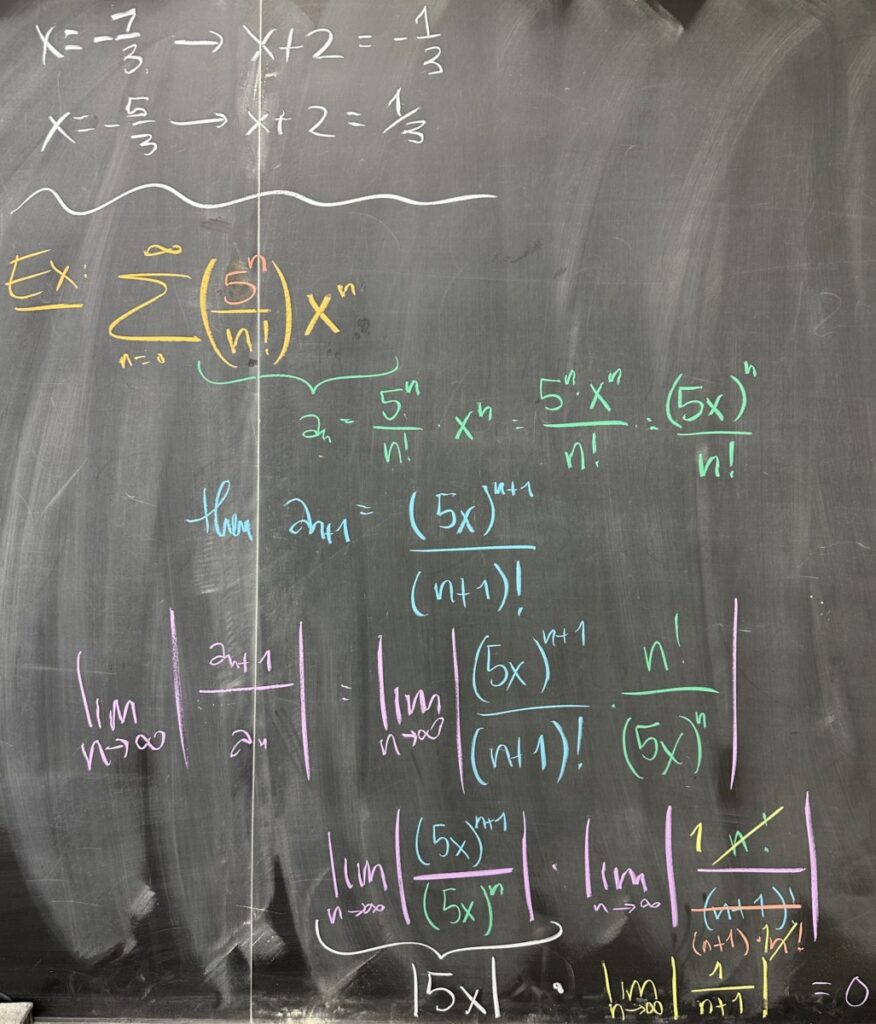
In our third example, we see how factorials dominate geometric factors. We pursue the usual process:
- Set up the limit for the Ratio Test.
- Rearrange the factors to align the ones that are similar.
- Compute the limits separately then multiply.
Our limit ends up being zero, with no remaining \(x\), but what does this mean?
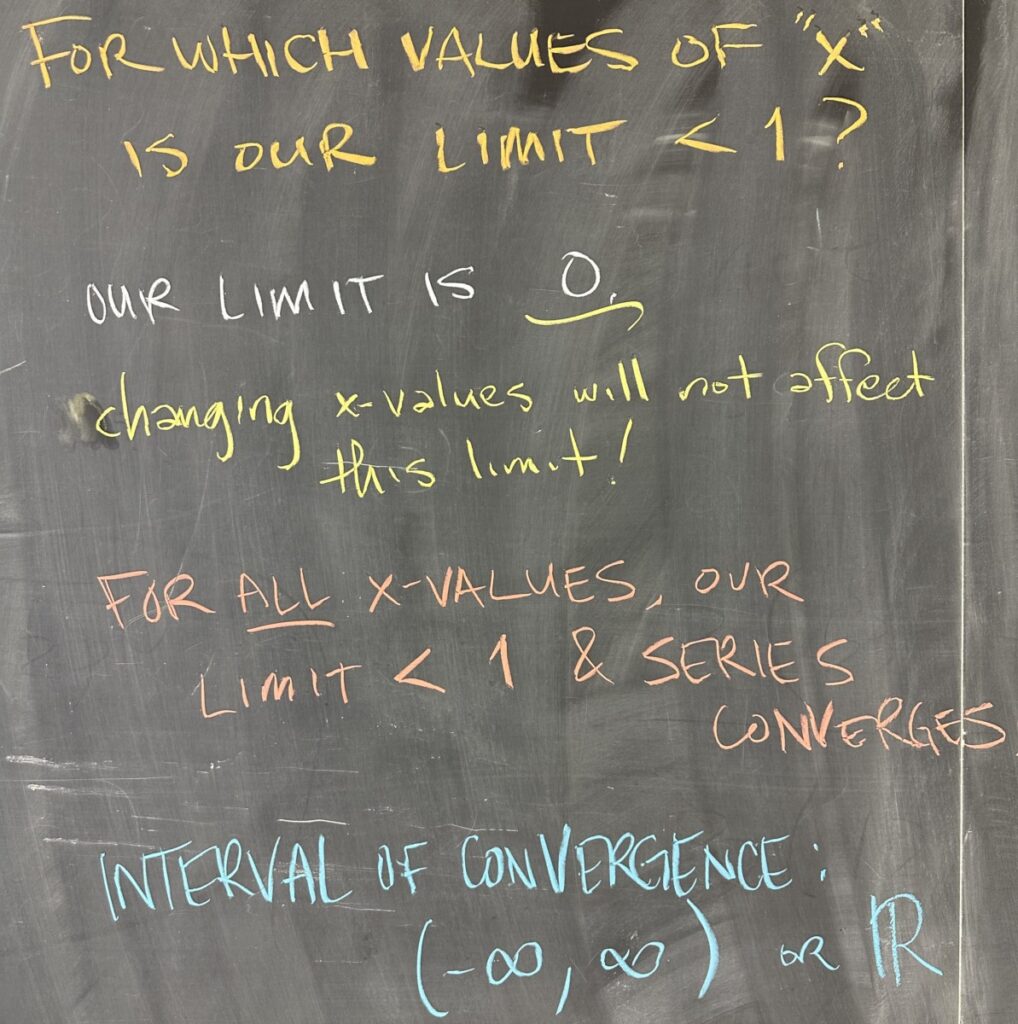
Our limit is zero no matter what value we use for \(x\). And zero is less than one, again no matter what value we use for \(x\). So our power series converges for ALL values of \(x\).

We wrapped up the lesson by reflecting on how we can approach any series that we want to analyze.
- Always start by considering the sequence, and we only proceed if the limit of the sequence is zero. If the limit is not zero, then the Divergence Test applies.
- If the sequence has limit zero, then the series still may or may not converge.
- We have a lot of tests at our disposal — maybe we recognize a specific form:
- Geometric: \(\displaystyle\sum^\infty a r^n\)
- p-Series: \(\displaystyle\sum^\infty \frac{1}{n^p}\)
- Alternating: \(\displaystyle\sum^\infty (-1)^n b_n\)
- If we don’t have one of these specific forms, we can:
- use L.C.T. if all of our terms are polynomial
- use Ratio Test if we have geometric factors or factorials present




Recent Comments