Series – Limit Comparison Test

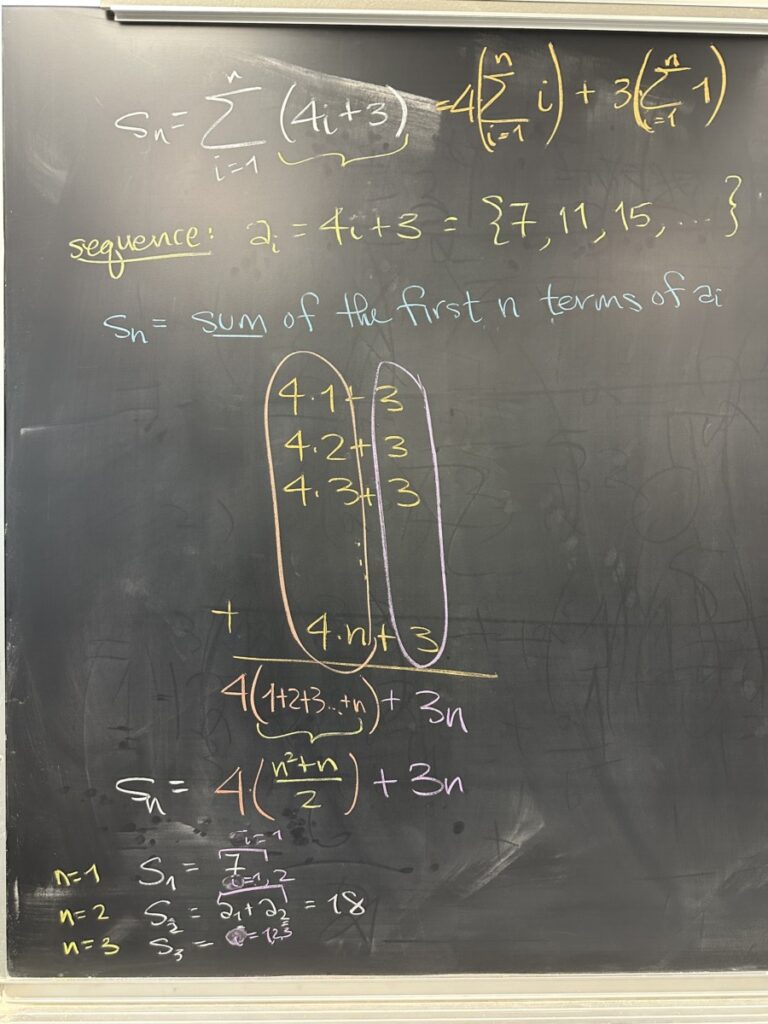
The first question on today’s quiz asked you to find a closed form for the sequence of partial sums (for the sequence \(a_i = 4i+3\)). Whenever we are considering sequences of partial sums (a.k.a. series), we must understand that the index for the partial sum \(n\) represents a range for \(i\) in the original sequence.

For example, when \( n = 3 \), \(i\) must start over at 1 and continue up to to 3. \(s_3\), then, is the sum of the results: \(a_1 + a_2 + a_3\).

The second question was not intended to be a trick question — it is ESSENTIAL that everyone realizes the equivalence of these phrases:

1. The sequence \(a_i\) has a limit.
2. \(\displaystyle\lim_{i\to\infty} a_i = L\)
3. The sequence \(a_i\) converges (to \(L\))

Here we distinguish between the convergence of a sequence and its corresponding series.

A sequence is an ordered list of numbers — often (for us) given by a formula (function) whose inputs are the index (position in the sequence) and whose outputs are the value in that position.

The sequence of partial sums is also a sequence, but it must be formed from another sequence! The reason I use a different index, \(n\), for the partial sums than the index, \(i\), for the sequence is to draw attention to this difference!

The word “series” can be used interchangeably with the sequence of partial sums OR its limit! Either way, we are talking about the values of an infinitely long sequence, or we are talking about the limit for these values (whether it exists or not).

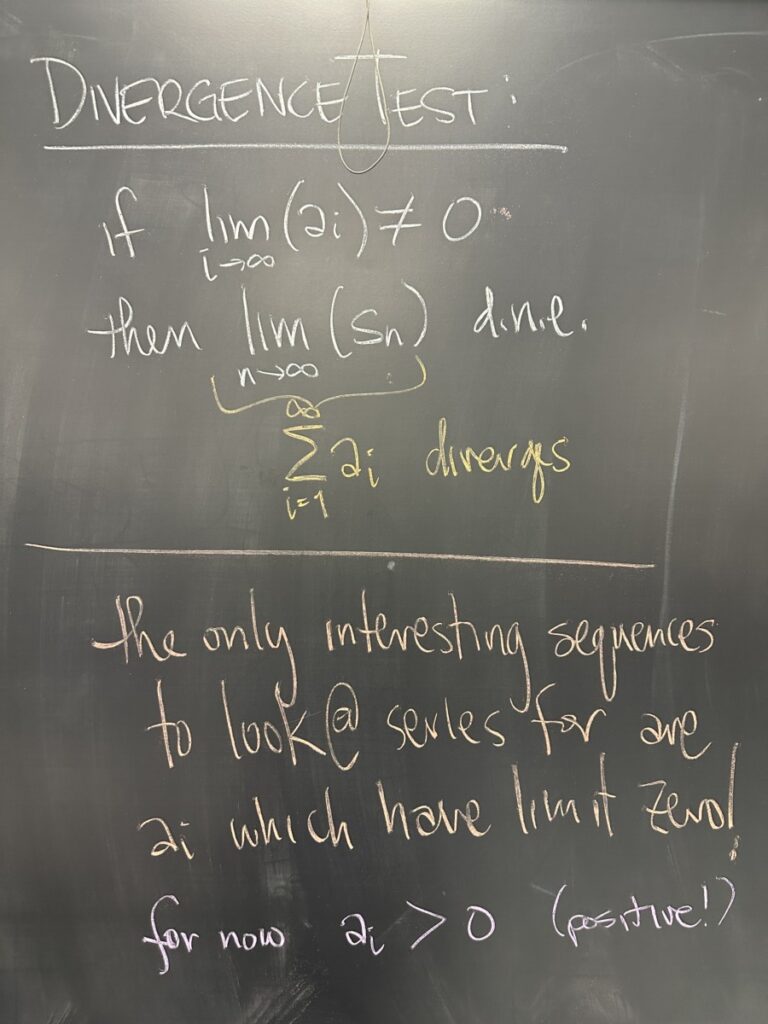
Remember that the Divergence Test tells us that starting with an \(a_i\) that does NOT converge to zero means that its series \(\displaystyle\sum^{\infty} a_i\) cannot converge!

\(\displaystyle \lim_{i\to\infty} a_i \neq 0\) means \(\displaystyle \sum^{\infty} a_i = \lim_{n\to\infty} s_n\) doesn’t exist (is divergent).

So series have NO chance of converging unless the limit of their sequence is ZERO!

Of course it is not enough for the sequence to approach zero. There are sequences that approach zero whose series diverge — AND — there are sequences that approach zero whose series converge.

So, if we’re looking at sequences that approach zero, that includes \(a_i = i^p\) for all \(p < 0\). An easier way of looking at that is \(a_i = \frac{1}{i^p}\) for all \(p > 0\).

As was just mentioned, some of these sequences have convergent series and others have divergent series. The p-test makes this specific:

1. If \(p \leq 1\) then the series \(\displaystyle \sum^{\infty} \frac{1}{i^p}\) diverges.
2. If \(p > 1\) then the series \(\displaystyle \sum^{\infty} \frac{1}{i^p}\) converges.

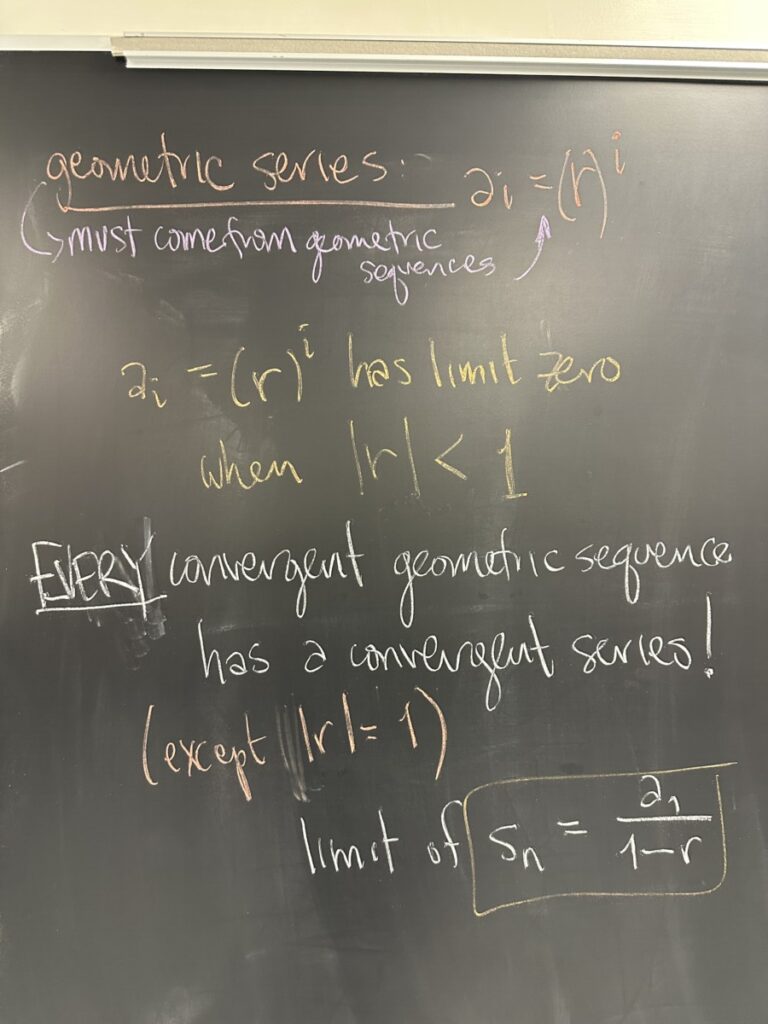
Geometric series (those that approach zero) approach zero even faster than p-series. That means if a geometric sequence approaches zero, its series MUST converge!

What’s more is that we KNOW the value of the infinite sum for convergent geometric series — \(\displaystyle\sum_{i=1}^{\infty} a_1 r^{i-1} = \frac{a_1}{1-r}\)

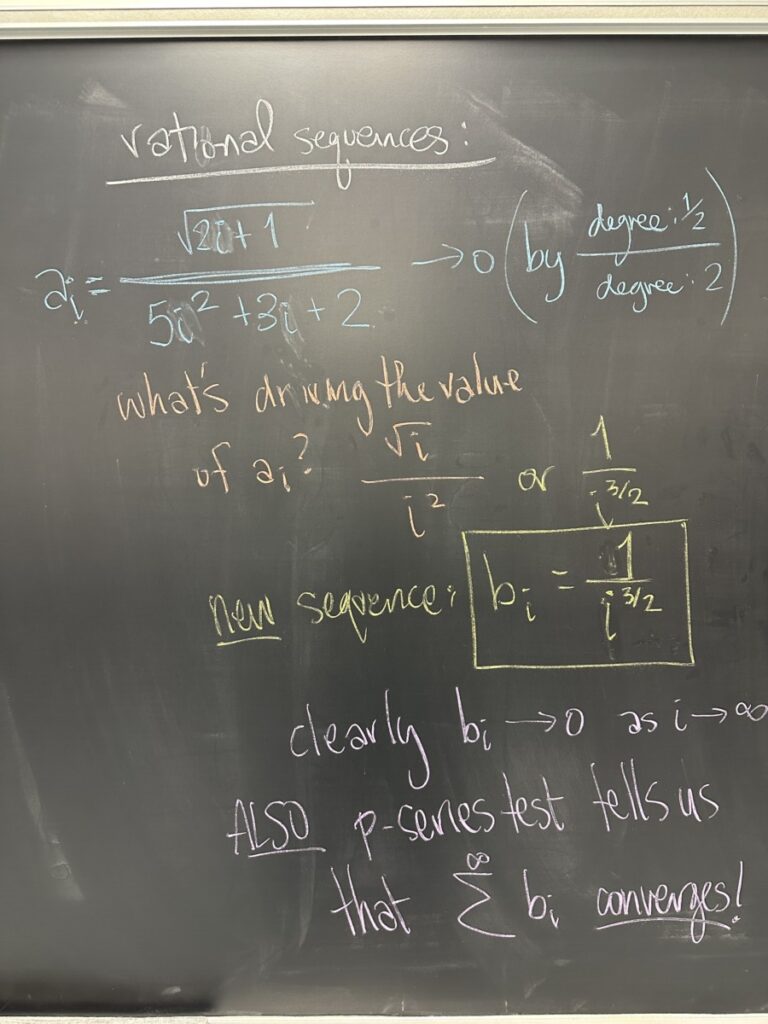
So, we will often encounter rational sequences such as this example. By looking at the highest power terms in the numerator and denominator, we can tell whether or not this sequence will have limit zero. This should feel familiar, as its the same process applied to rational functions in finding horizontal asymptotes (a.k.a. limits).

In finding the relative powers of the numerator and denominator, we end up finding a p-sequence (over-simplified form of our original \(a_i\)). Now we have our original (messy) \(a_i\) and our way-simple \(b_i\). Even better, our \(b_i\) has a convergent series (by the p-series test).

If only we had a way to relate the series for \(b_i\) back to the series for \(a_i\)!

Enter the latest test: The Limit Comparison Test (LCT)

The LCT says that if we have two sequences that (eventually, as \(i\) grows to infinity) behave like constant multiples of each other, then their series will have the same behavior. In other words, if one of the two sequences has convergent series, so will the other! And vice versa!

What’s even better is that our earlier process of over-simplifying our rational sequence produces exactly this type of paired sequences. Since our \(b_i\) has the same relative powers as our original \(a_i\), we should expect that the limit of \(\dfrac{a_i}{b_i}\) is a non-zero constant.

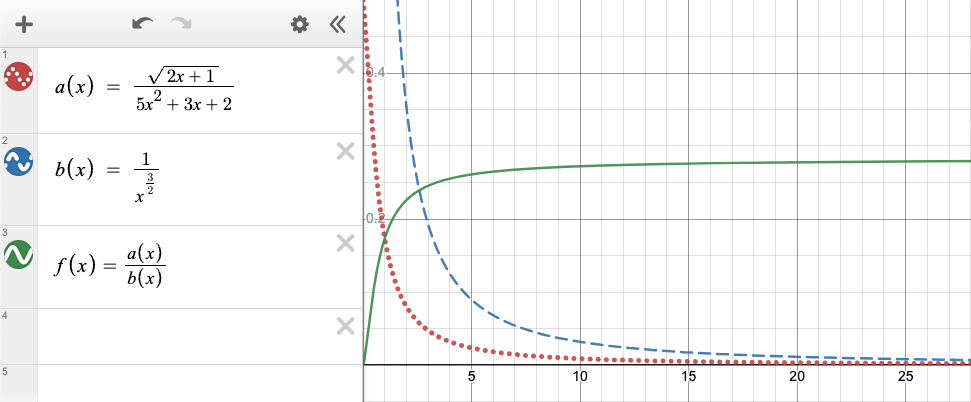
Both the a and b “sequences” have limit zero. Their ratio clearly has non-zero limit. (desmos link)

And finally, since the series from \(b_i\) is a p-series, we can quickly identify that \(p = \frac{3}{2} > 1\) so both series \(\displaystyle \sum^{\infty} a_i\) and \(\displaystyle \sum^{\infty} b_i\) converge!