
Well, today’s quiz didn’t go as expected. (If you were there, you know.)
So, instead we did some examples together! Our first example is an alternating series, with absolute sequence \(b_n = \dfrac{2n^3-1}{\sqrt{9n^4-n}}\).
Our absolute sequence satisfied one of the three requirements for the Alternating Series Test. It is positive, but it is not monotone decreasing, and it does not have limit zero.
As a result, the Alternating Series test does NOT apply (inconclusive).
However, because the limit of the absolute sequence diverges, the limit of the original \(a_n\) sequence ALSO diverges. And when that happens, we appeal to the Divergence Test — which says that when \(a_n\) doesn’t converge to zero (ours doesn’t converge AT ALL), the corresponding series \(\displaystyle\sum^\infty a_n\) diverges.

Our second “example” is also an alternating series, with absolute sequence \(b_n = \dfrac{5n+2}{2n-1}\). This absolute sequence satisfies two of the three requirements for Alternating Series Test. It is positive and monotone decreasing — however, it does NOT have limit zero. Again, since we do not meet all three requirements, the Alternating Series Test does not apply (inconclusive). Like the previous example, though, the non-zero convergence of the absolute sequence means that the alternating sequence will diverge. And again, the Divergence Test will apply, telling us that the original series diverges.
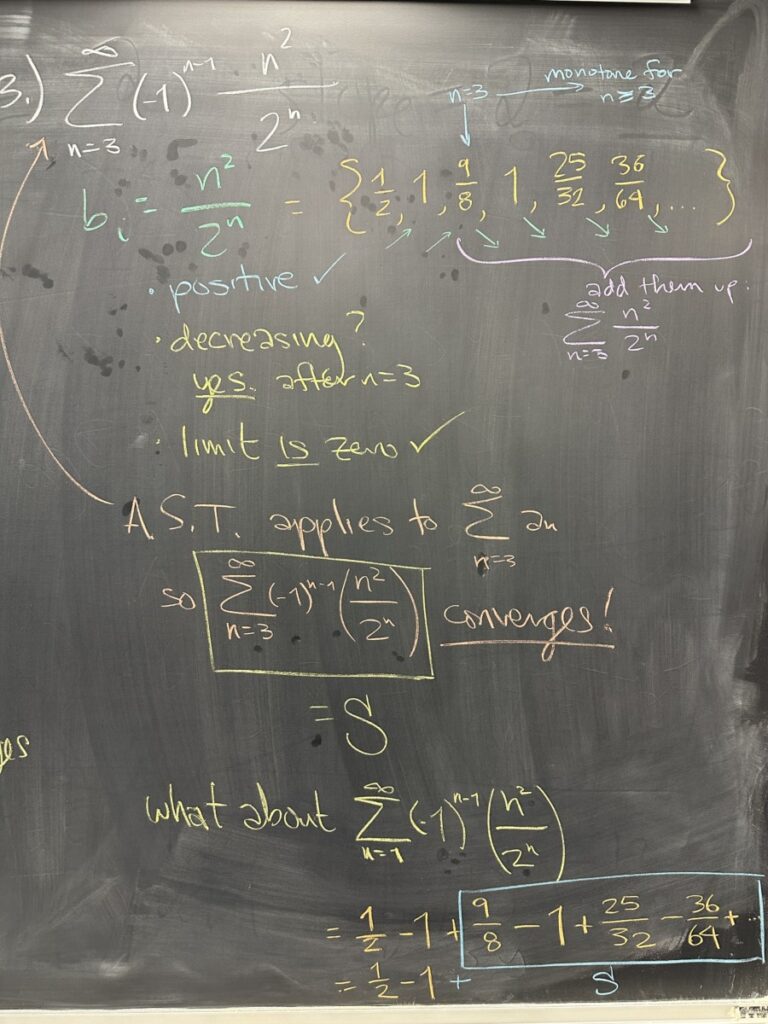
The third example is again an alternating series, with absolute sequence \(b_n = \dfrac{n^2}{2^n}\). Here we see a series that is starting somewhere after \(n = 1\). What this means is that we are ignoring \(a_1\) and \(a_2\) for the purposes of determining this series’s convergence or divergence.
This is important because the \(b_n\) sequence is positive and has limit zero — but it isn’t monotone decreasing. However, the sequence does start being monotone decreasing at \(n = 3\). Because of this, we can say that \(b_n\) IS monotone decreasing for \(n \geq 3 \).
Since \(b_n\) satisfies the conditions of the Alternating Series Test (for \(b \geq 3\)), we can conclude that the original alternating series does converge.
Moreover — the series converges even if we start at \(n = 1\) since that infinite sum is the same as the one we just showed convergence for (\(n \geq 3\)), with just a couple extra terms added. (See the bottom of the above picture)

However, if we want to determine whether the alternating series from the last example was conditionally or absolutely convergent — we must be able to say whether or not the series \(\displaystyle\sum^\infty \frac{n^2}{2^n}\) is convergent or divergent.
In order to do that, we will need a new test.
We first consider geometric series and when they converge. Remember that geometric series converge whenever their sequences converge to zero. This is because geometric sequences will converge to zero faster than any p-sequence. (The “most powerful” p-sequences — any \(p > 1\) — all have convergent series, and our geometric sequences will approach zero even faster!)
So, what conditions cause the geometric sequence to converge to zero? That happens whenever the absolute value of the common ratio is less than 1. We will see this condition reflected in the new test we are about to learn.
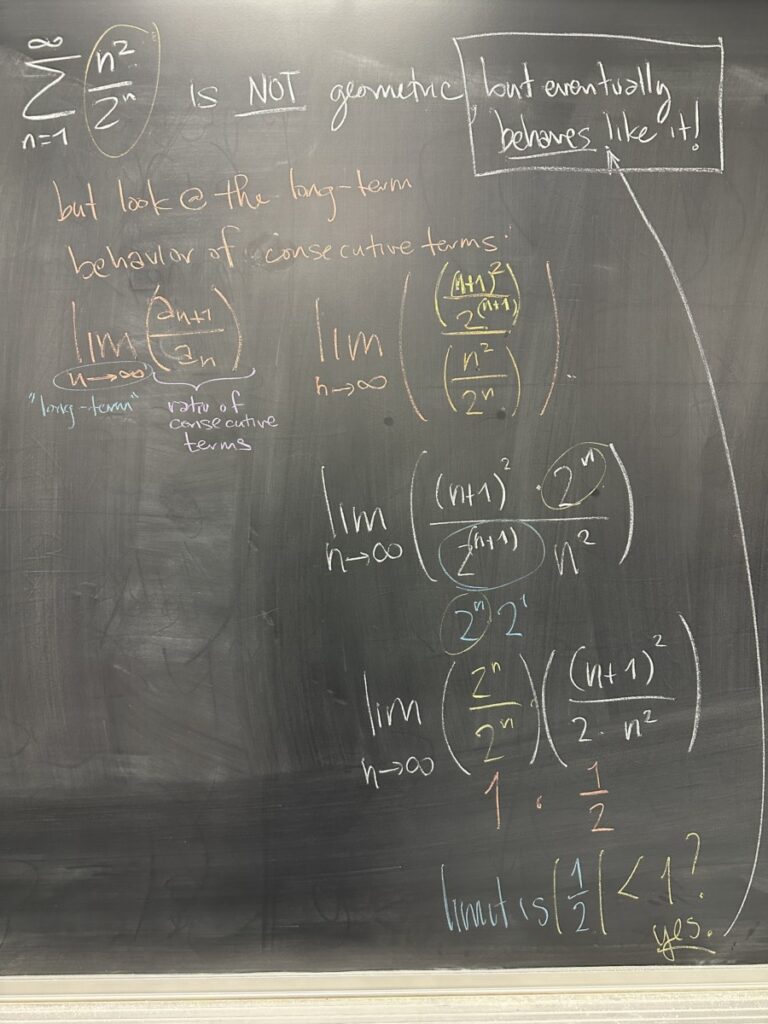
We knew that \(\dfrac{n^2}{2^n}\) had limit zero because the denominator is geometric — which has higher “power” than any polynomial term (including \(n^2\), as in our numerator). As a result, we expect the long-term behavior of this sequence to be “almost” geometric.
\(\left\{ \dfrac{n^2}{2^n} \right\}\) does NOT have a common ratio, but if we look at the ratio of consecutive terms as \(n\) gets “really large” (i.e. as \(n \to\infty\)), we should expect to see the ratio approaching a common-ish ratio.
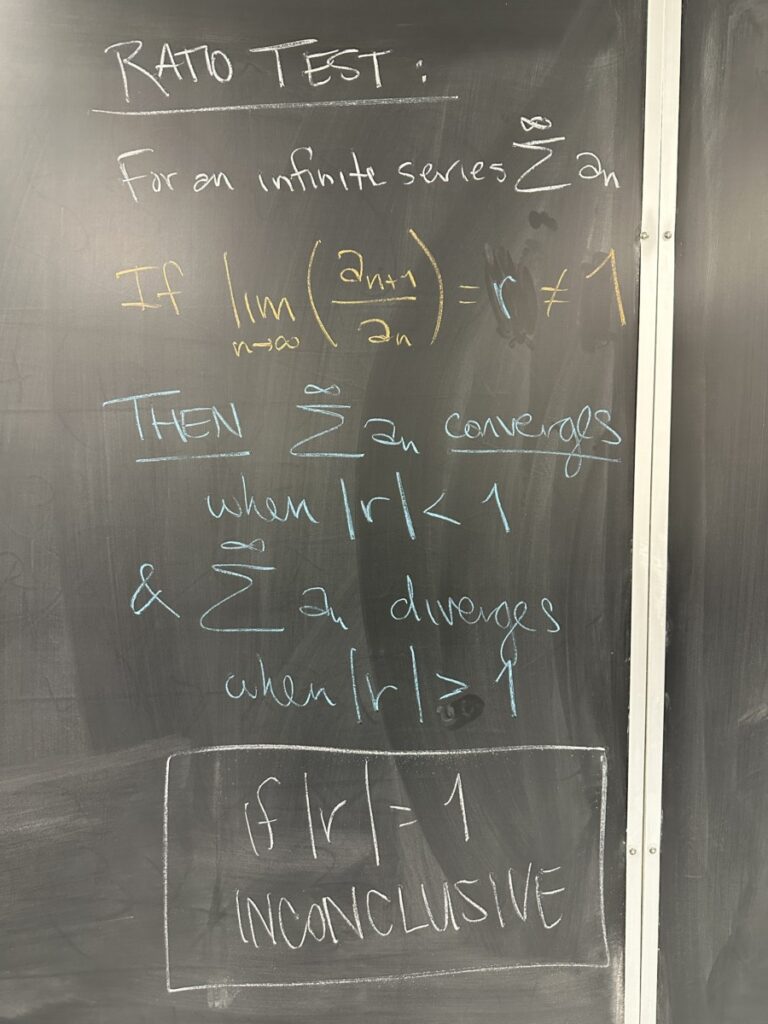
The ratio test tells us that if a sequence has a common-ish ratio, then it converges or diverges just like an actual geometric series. In other words, if the commonish ratio has absolute value less than one, the “almost geometric” series converges. And if the commonish ratio has absolute value greater than one, well, we should never have gotten here, because the sequence isn’t going to zero and we should have used the Divergence Test in the first place. But the Ratio Test is here to back us up and it says that if the commonish ratio has absolute value greater than one, the “almost geometric” series diverges (by Ratio Test AND by Divergence Test).
Back to our example, we found that \(\displaystyle\lim_{n\to\infty} \dfrac{a_{n+1}}{a_n} = \dfrac{1}{2}\). This common-ish ratio has absolute value less than one, so we can conclude (by the Ratio Test) that the corresponding series, \(\displaystyle\sum^\infty \dfrac{n^2}{2^n}\) is convergent.
Bonus points: Is the third example (above) conditionally convergent or absolutely convergent? If you can give the correct answer on Tuesday’s quiz, I’ll give you bonus points. Be ready for it, I won’t restate the entire problem on the quiz.
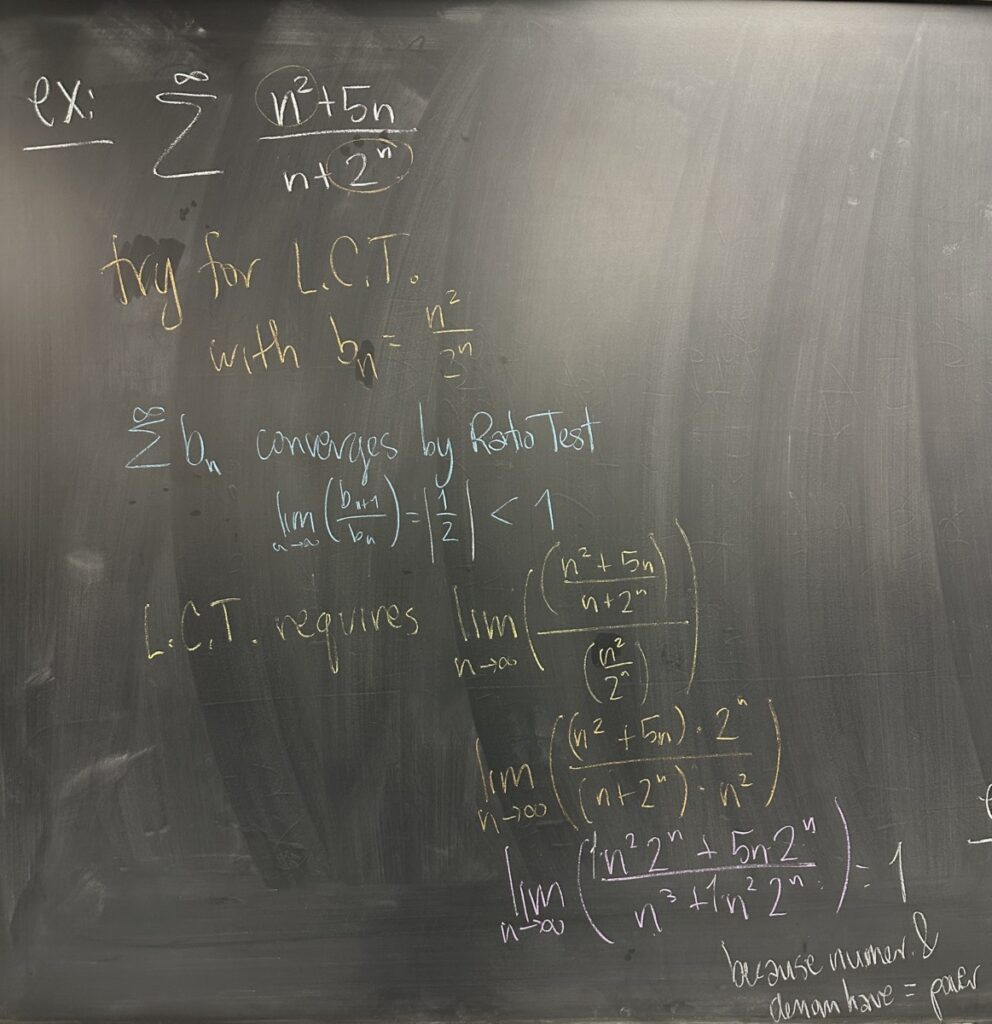
Moving on to another example, we consider what looks to be a mostly polynomial sequence, but it has a geometric term in it!
As with our previous uses of the L.C.T., we look to “over-simplify” the given sequence by keeping only the highest power terms. This example is comparable to the sequence (again) \(b_n = \dfrac{n^2}{2^n}\). For L.C.T. to apply, we must satisfy its condition: \(\displaystyle\lim_{n\to\infty} \frac{a_n}{b_n} = L \neq 0\).
The majority of the work shown here is in finding this limit. Our result is that the limit is one, and therefore the LCT applies to our \(a_n\) and chosen \(b_n\).
Since LCT applies, the two series either both converge or both diverge.
We had already shown that \(\displaystylesum^\infty b_n\) is convergent, so LCT tells us that our original series must converge as well.
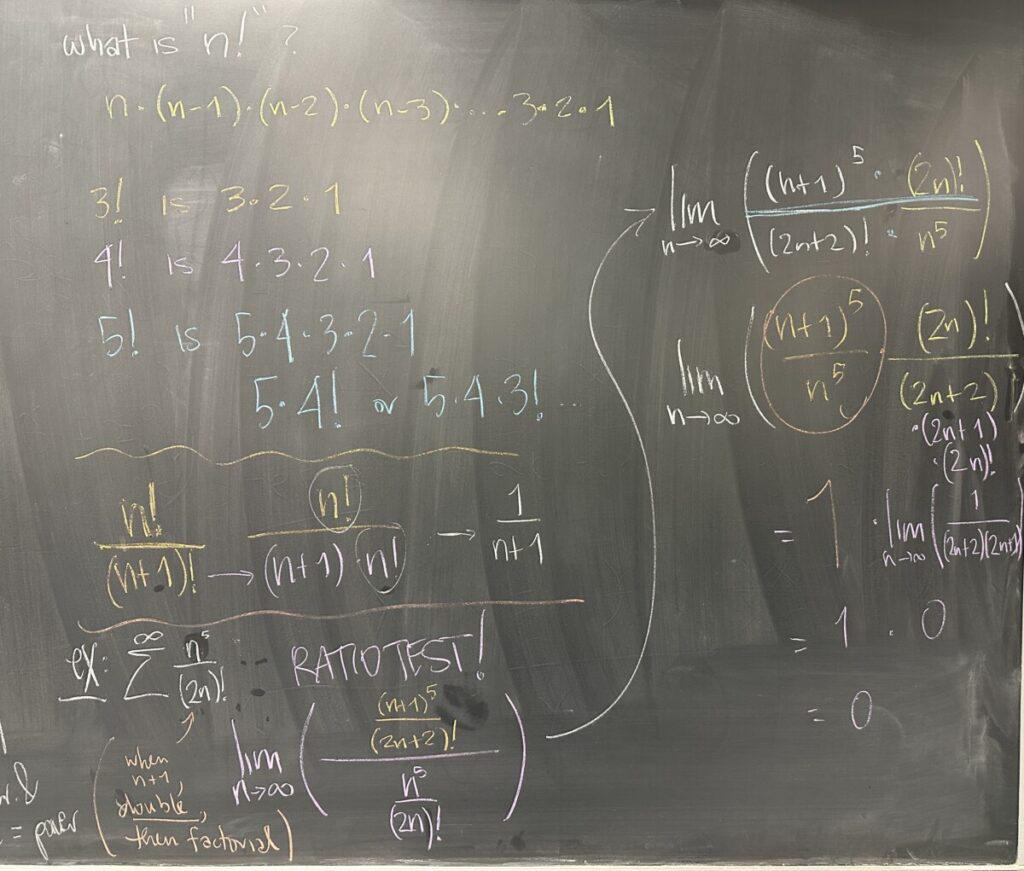
Our final example of the day intends to show how the Ratio Test applies to pretty much any sequence that makes use of factorial.
First, we looked at the behavior of the factorial; then we looked at how factorials can interact (particularly when reducing fractions).
In our final example, we applied the ratio test to \(a_n = \dfrac{n^2}{(2n)!}\). The ratio test requires both \(a_n\) and \(a_{n+1}\). Be very careful when finding \(a_{n+1}\)!
Once we had both, we constructed the ratio and went after finding the limit: \(\displaystyle\lim_{n\to\infty} \frac{a_{n+1}}{a_n} \). A common tactic when finding these limits is to align similar factors — factorials over factorials, polynomials over polynomials, etc. We also broke down the larger factorial until the point where we had identical factorials in the numerator and denominator. \((2n+2)! = (2n+2)(2n+1)! = (2n+2)(2n+1)(2n)!\)
After reducing, we found that the limit (our common-ish ratio) is zero. By the Ratio Test, we conclude that this series, \(\displaystyle\sum^\infty \dfrac{n^2}{(2n)!}\), is convergent.



Recent Comments