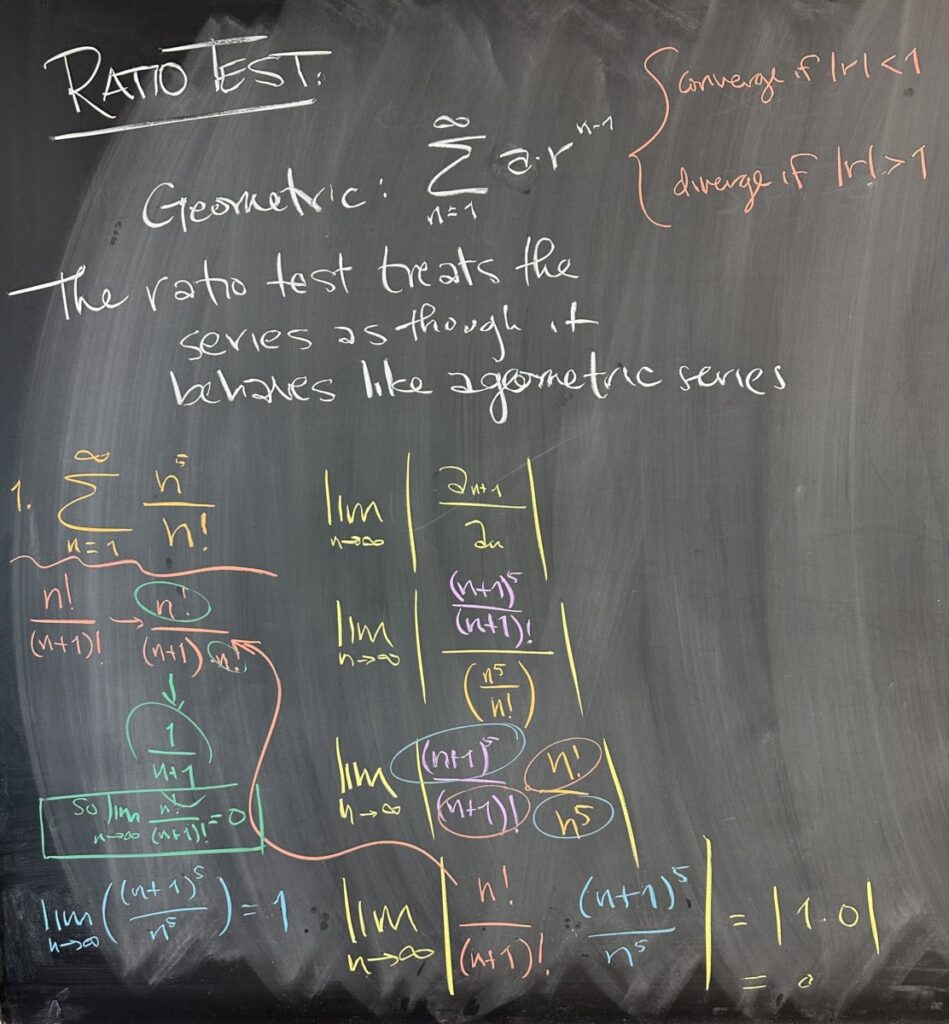
Before talking about today’s quiz, I asked the class to recall the motivation behind the Ratio Test. We will see many series with sequences that are “almost” geometric. That is to say, sequences that don’t have a strictly common ratio — but as n gets very large, the sequence has something very close to a common ratio. (In the last set of notes, I called this a “common-ish” ratio.)
So, when looking at the first problem from today’s quiz, not only were we told to use Ratio Test (in the instructions), but we also see factorial in the sequence. Because of this, we should instinctively turn to the Ratio Test to determine the convergence or divergence of the series.
The process follows the usual pattern:
- Find \(a_n\)
- Find \(a_{n+1}\)
- Simplify the ratio \(\frac{a_{n+1}}{a_n}\) and take the limit
Now, because the Ratio Test compares the absolute value of our limit, some books (and many internet tutors) will apply the absolute value before taking the limit. It does not matter which order you do it in.
In our case, we found that the limit of the ratio was ZERO! (Intuitively, this means that our sequence converges to zero even faster than a geometric series — which is plenty fast enough for convergence of the corresponding series!)
Since our limit, \(\displaystyle\lim_{n\to\infty} \left|\frac{a_{n+1}}{a_n}\right| = 0\), has absolute value less than one, we conclude that the original series \(\displaystyle\sum^\infty \frac{n^5}{n!}\) converges by the Ratio Test.
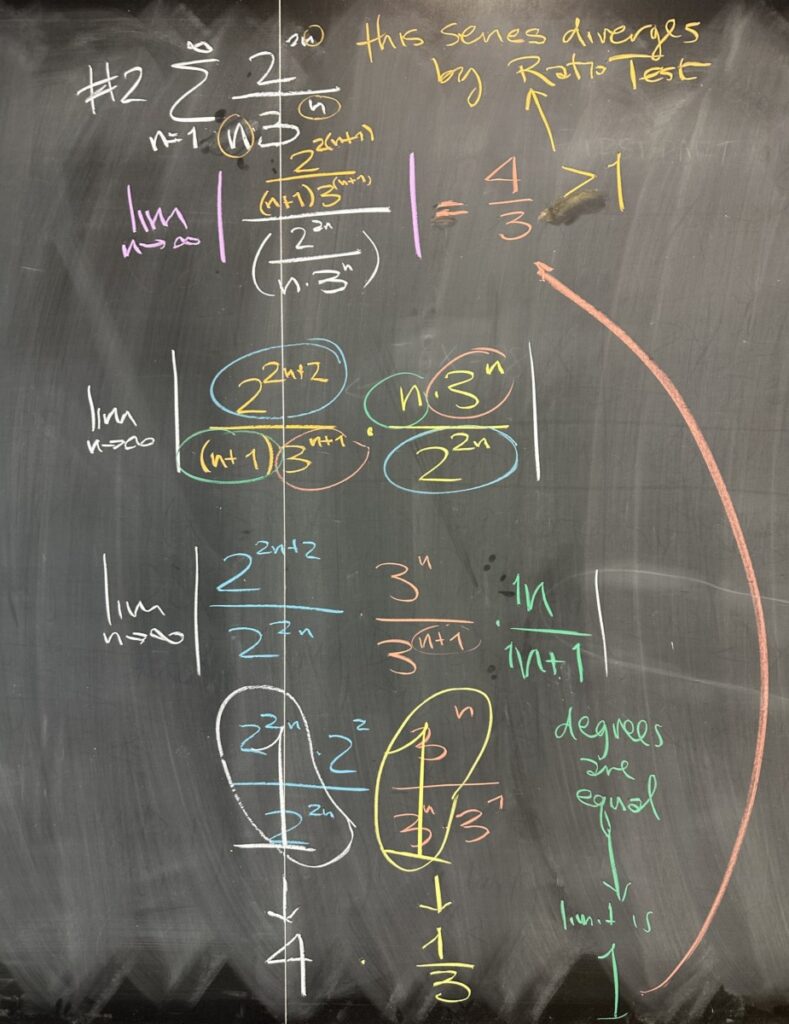
In our second example, we again apply the Ratio Test. Of course, in this case, our instructions explicitly told us to apply the Ratio Test — but because we see multiple geometric factors, \(2^{2n}\) and \(3^n\), our intuition should point us towards the Ratio Test anyhow.
Again, applying the same strategy:
- Identify \(a_n\)
- Replace \(n\) with \((n+1)\) to get \(a_{n+1}\)
- Simplify and rearrange the ratio
- Find the limit, and compare its absolute value to 1
Note that we had to be very careful with our \(2n\) exponent.
We ultimately computed the limit to be \(\frac{4}{3}\), which has absolute value greater than 1. As a result, we can conclude that our series diverges by the Ratio Test.
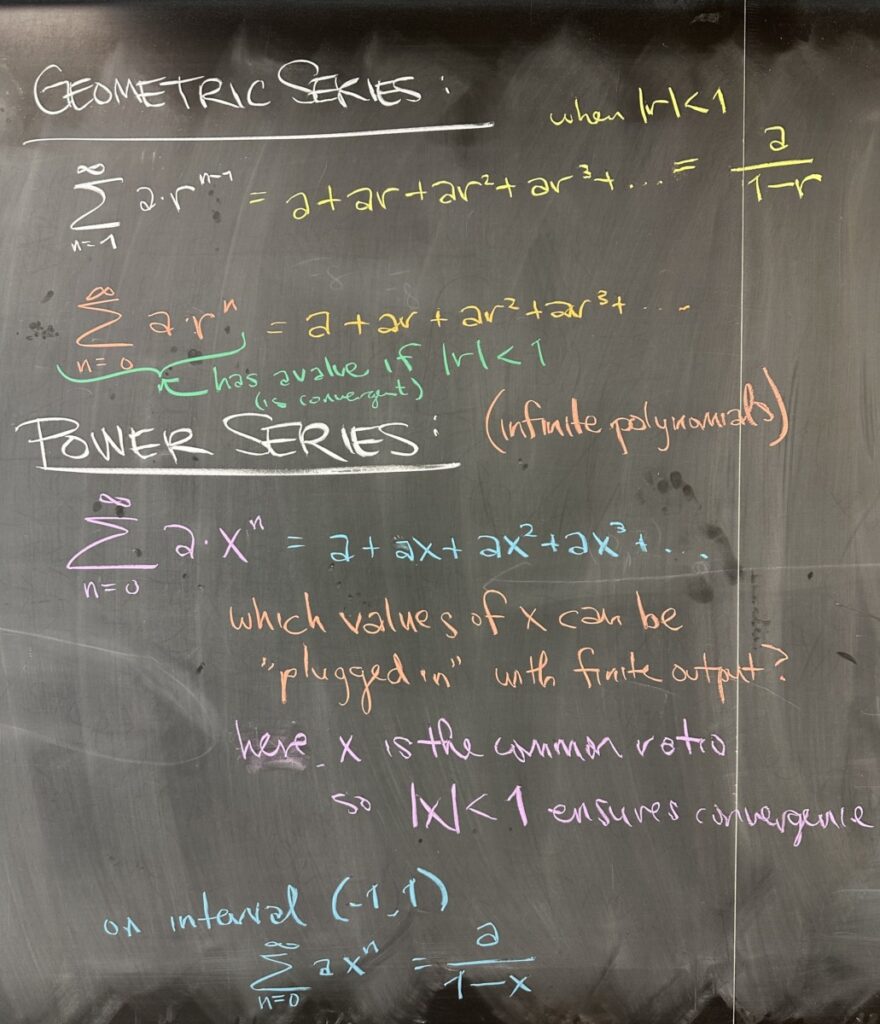
Again, returning to geometric series as our foundation for Power Series, we considered two different ways of writing the same series. The first starts with \(n=1\), which we have been seeing a LOT. The second representation worked out to give use an identical sum, but started instead with \(n=0\). You will want to pay close attention to the starting index — and I suggested (verbally) that whenever you start working on a series, you should think about what the pattern of the first several terms are. Write it out if you need to!
So, we started by looking at the most basic power series that there is: \(\displaystyle\sum^\infty_{n=0} ax^n\). When we wrote out the first several terms (as I recommended), we see what looks to be a polynomial. The only thing is, this polynomial doesn’t have a degree! The powers of \(x\) only continue to rise as \(n\to\infty\). When we see power series, we should think of them as infinite polynomials.
With polynomials, we typically have a domain of \((-\infty,\infty)\) — but because these “polynomials” (power series) are infinite, they only have an output when the input (\(x=\) some number) causes the series to converge.
Fortunately, for this example, our power series is strictly geometric (with common ratio \(x\)). And for any power series, we know that the series converges if (and only if) the common ratio has absolute value less than one. In other words, for our series, if \(\left|x\right| < 1\).
We say that the resulting interval, \(\left(-1,1\right)\), is the “interval of convergence” for the power series \(\displaystyle\sum^\infty_{n=0} ax^n\).
Because our power series is strictly geometric, we know that any other value of \(x\) will cause the resulting series to diverge.
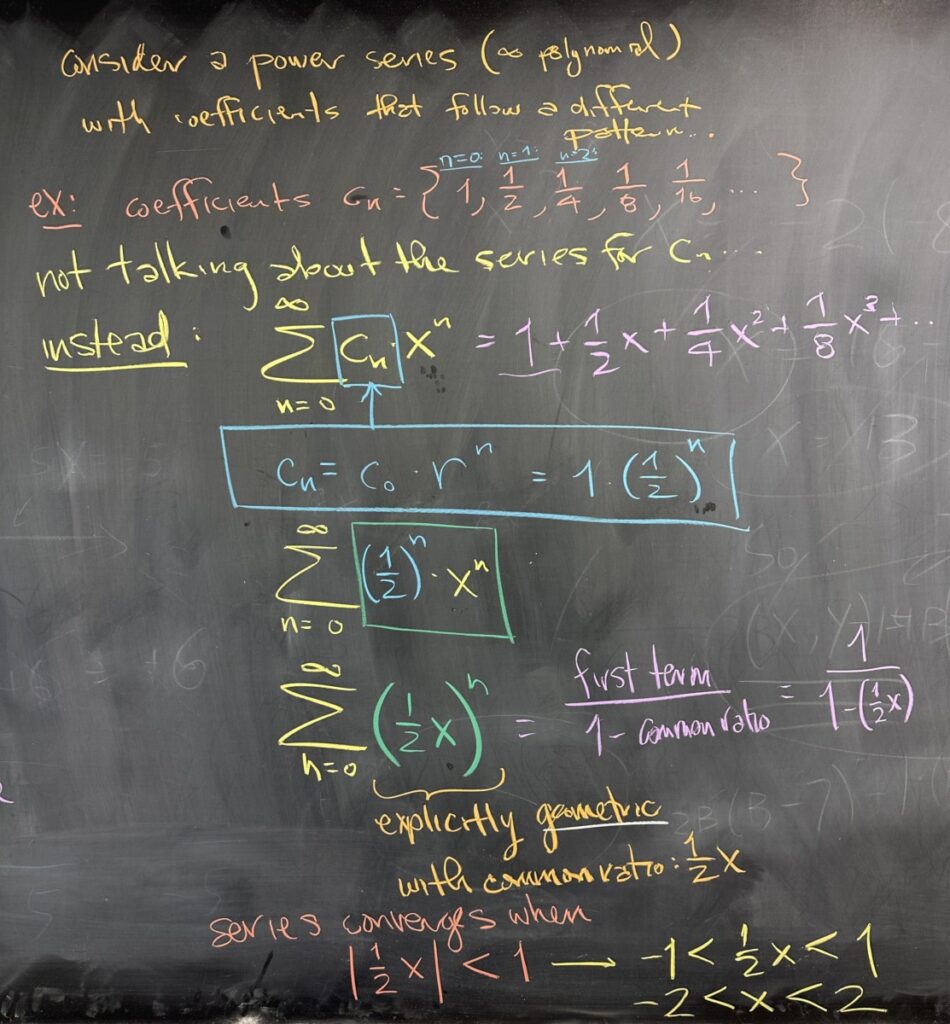
The previous example was the most simplistic of all power series, because the coefficient of each term in the polynomial was constant.
In this next example, we consider a power series with coefficients that follow a different pattern. I pointed out in class that we often refer to the coefficient sequence as \(\left\{c_n\right\}\) (with \(c\) for coefficient). Just like we use \(f, g, \text{and} \, h\) to refer to different functions, we can use different letters, \(a, b, c\), to refer to different sequences.
In this example, the sequence of coefficients is also geometric. We write the closed form for \(c_n\) and then rearrange the closed form for our power series.
Because our coefficients follow a geometric series, and the \(x^n\) factors are also geometric, their product will be strictly geometric as well.
As with the previous example, we know that geometric series converge if (and only if) the common ratio has absolute value less than one. In this example, our common ratio is \(\frac{1}{2}x\). When we unravel the absolute value inequality, we end up with the interval \(\left(-2,2\right)\) as our interval of convergence.
Take some time to think about what happens when we choose a value for \(x\) from this interval. Replacing \(x\) with the chosen value creates a geometric series, what would the common ratio be with \(x\) replaced?
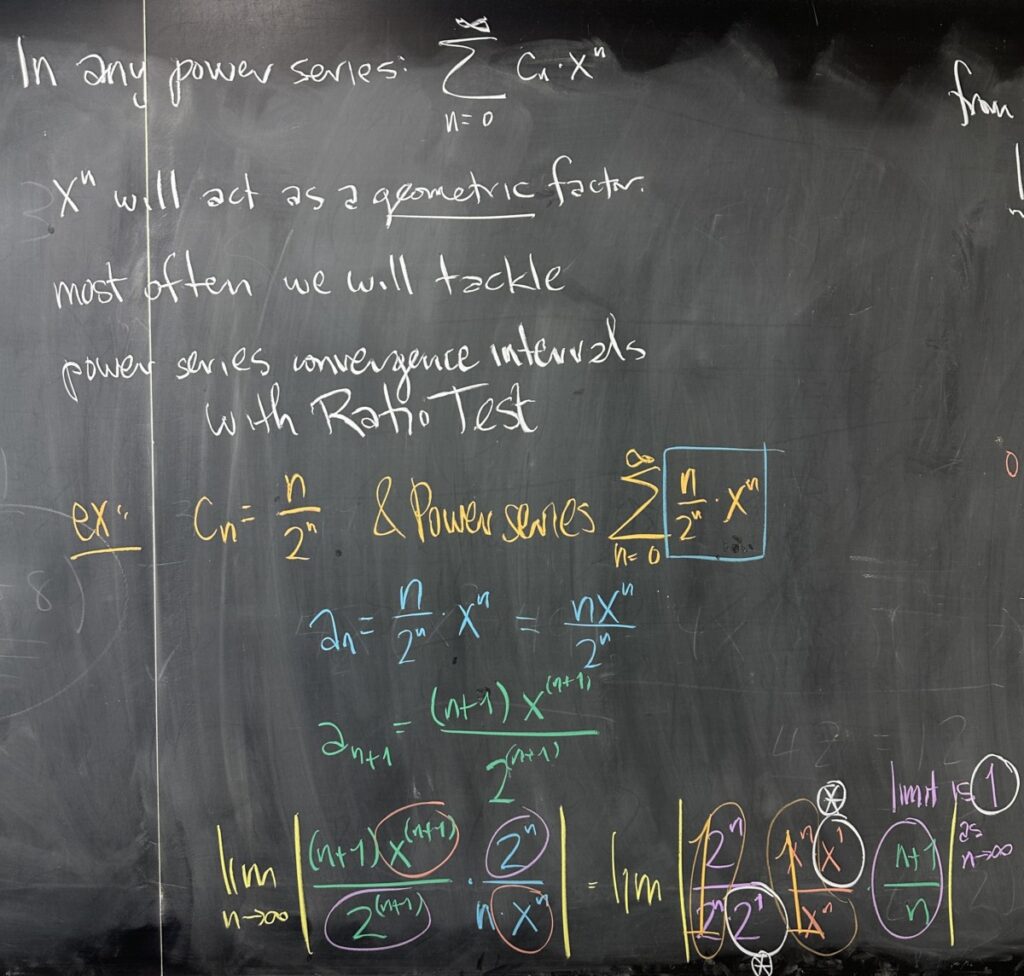
Take a moment to reinforce the connection between Power Series (those with (x^n)) and the Ratio Test. Our power series will always be at least “nearly” geometric — if not strictly geometric.
In our third, and final, example — we look at a coefficient sequence that is not strictly geometric.
Since our coefficients are not strictly geometric, we must use the Ratio Test (there’s no common ratio). We follow the usual procedure:
- Identify \(a_n\)
- Find \(a_{n+1}\)
- We rearrange and reduce the ratio \(\dfrac{a_{n+1}}{a_n}\)
- The final limit must include \(x\), and ours does — the product of our individual limits is \(\frac{1}{2}\cdot x \cdot 1\)
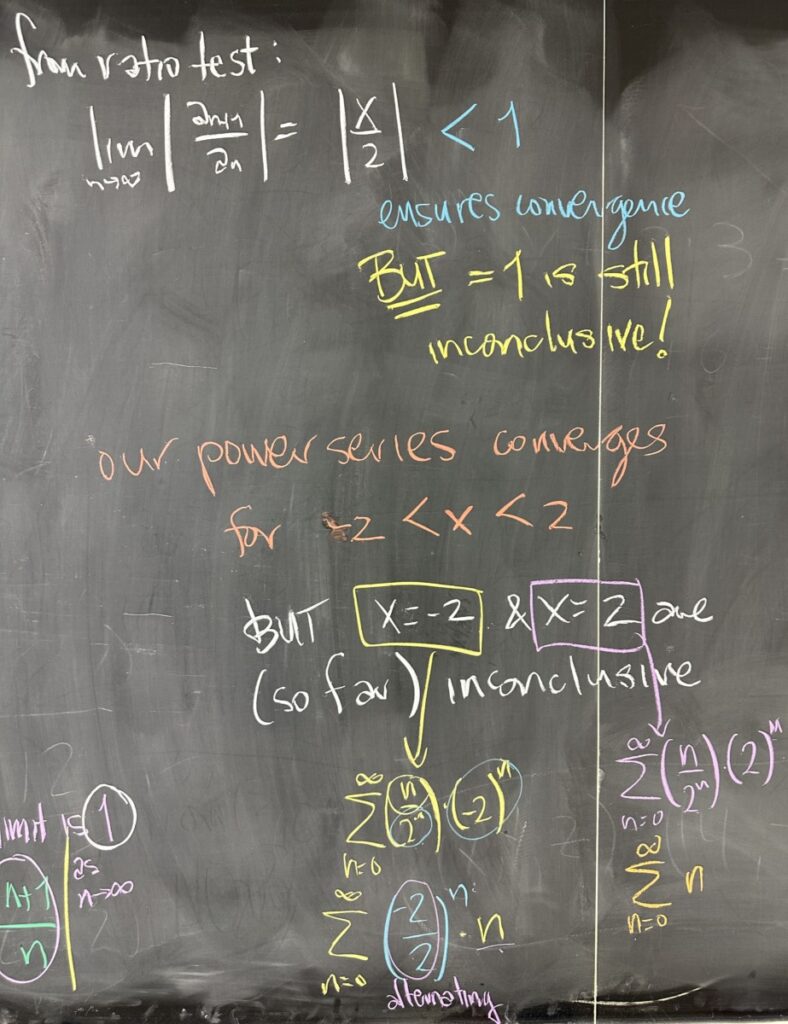
Since our “common-ish” ratio is \(\dfrac{x}{2}\), the Ratio test tells us three things:
- The power series converges when \(\left|\dfrac{x}{2}\right| < 1\).
- The power series diverges when \(\left|\dfrac{x}{2}\right| < 1\).
- We don’t know what happens when \(\left|\dfrac{x}{2}\right| = 1\), the Ratio Test is inconclusive.
So, we know our interval of convergence will at least be \((-2,2)\) — but either of the endpoints, \(x = \left\{-2,2\right\}\), may or may not cause the series to converge. What we do know is that the Ratio Test is inconclusive for \(x=\left\{-2,2\right\}\), and we will need to use another test or tests.
Consider \(x=2\), we get the series \(\displaystyle\sum^\infty_{n=0} \left(\frac{n2^n}{2^n}\right) = \sum^\infty_{n=0} n\). This series diverges by the divergence test. (\(a_n = n\) and \(\displaystyle \lim_{n\to\infty} a_n = \lim_{n\to\infty} n = \infty\), not zero.) So \(x=2\) will not be included in our interval of convergence (clearly, because it causes the series to diverge).
If we instead consider \(x=-2\), we get the series \(\displaystyle\sum^\infty_{n=0} \left(\frac{n(-2)^n}{2^n}\right) = \sum^\infty_{n=0} (-1)^nn\). While this is an alternating series, it doesn’t matter because the sequence \(\left\{(-1)^nn\right\}\) does not converge to zero. As a result, we know that the series for this endpoint also diverges (by Divergence Test).




Recent Comments