Quiz problems:
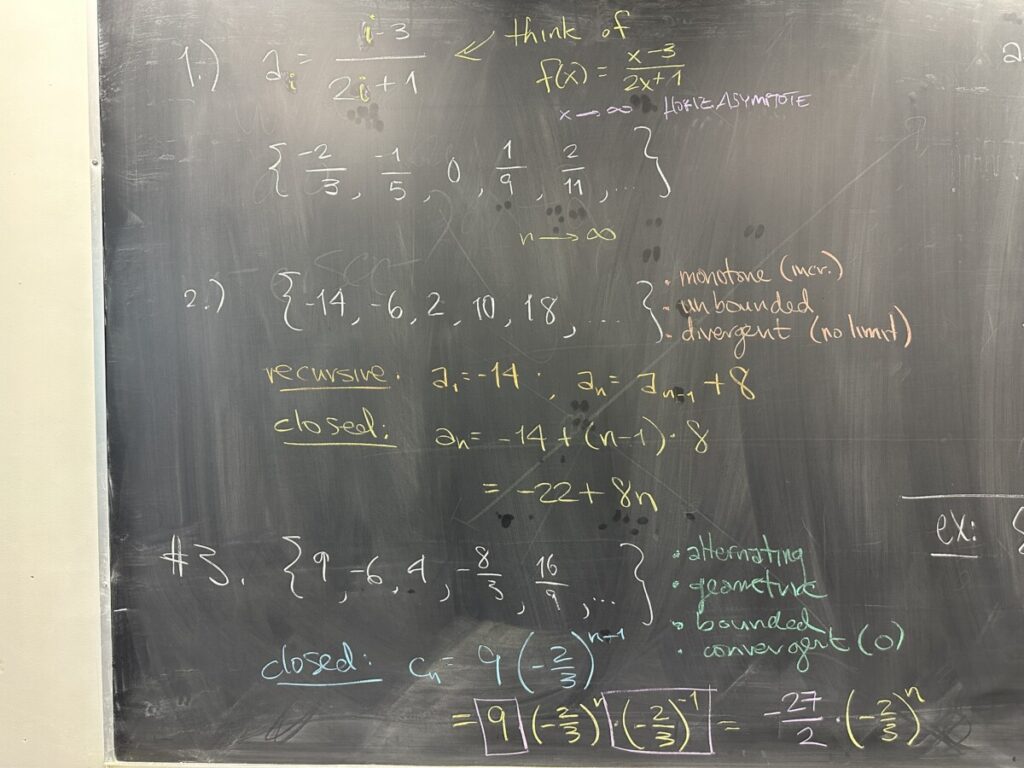
Even though sequences are not the same as functions, we can use our understanding of functions to draw conclusions about sequences. The first sequence on the quiz follows a rational function — we know that the rational function has a horizontal asymptote, and from this we can conclude that the sequence has a limit.
The second sequence is arithmetic, and the third sequence is geometric.

Take note: any sequence that converges must be bounded — this is NOT true in reverse. There are bounded sequences that do NOT converge (see these examples)
However, if a sequence is BOTH bounded AND monotone, then that sequence MUST converge.

Whenever we have a closed form for a sequence, we can consider it as a function — and as a result, we can determine the convergence or divergence of the sequence immediately.
We now turn to “series” (a.k.a. the sequence of partial sums), which is itself a sequence, constructed by taking sums of values from another sequence.

Because the series is sum of another sequence, we often will not have a closed form for the series.
The following is python code to create a sequence “a”, print the first 10 terms of the sequence “a”, and then print the first 10 terms of the series “a”
# geometric sequence "a"
# initial term = 3
# common ratio = 0.5
def a(x):
return 3 * 0.5 ** ( x - 1 )
# print the first 10 values in the "a" sequence
for i in range(1,11):
print(f"a_{i} = {a(i)}")
# print the first 10 terms of the "a" SERIES
sum = 0;
for i in range(1,11): sum = sum + a(i)
print(f"{i}th partial sum: s_{i} = {sum}")
Because we usually will NOT have a closed form for the series, we will only answer the question “does the limit EXIST?” rather than trying to answer “what IS the limit?”

To understand the behavior of the SERIES, we will rely on drawing implications from the behavior of the SEQUENCE. Here we start by considering the implications of looking at a series where all the sequence values are positive… in such a case our series is longer and longer sums of strictly positive numbers — which must grow with each additional summand! We conclude that the series is monotone increasing (the sum cannot shrink unless we added a negative number…)
Similarly, we consider what a convergent SERIES (for drawing the picture, we considered a positive SEQUENCE) must look like. If the SERIES is convergent, it must also be bounded. Then, by looking at the steps between (s_1) and (s_2), between (s_2) and (s_3), and so on… we see that those differences MUST be getting smaller (approaching zero) as the SERIES converges. We also note that the differences between consecutive partial sums are exactly the values of the SEQUENCE.
So the difference between consecutive values in the SERIES must approach zero, AND those differences are exactly the values of our SEQUENCE, so we conclude that any CONVERGENT SERIES must come from a SEQUENCE that has limit zero.
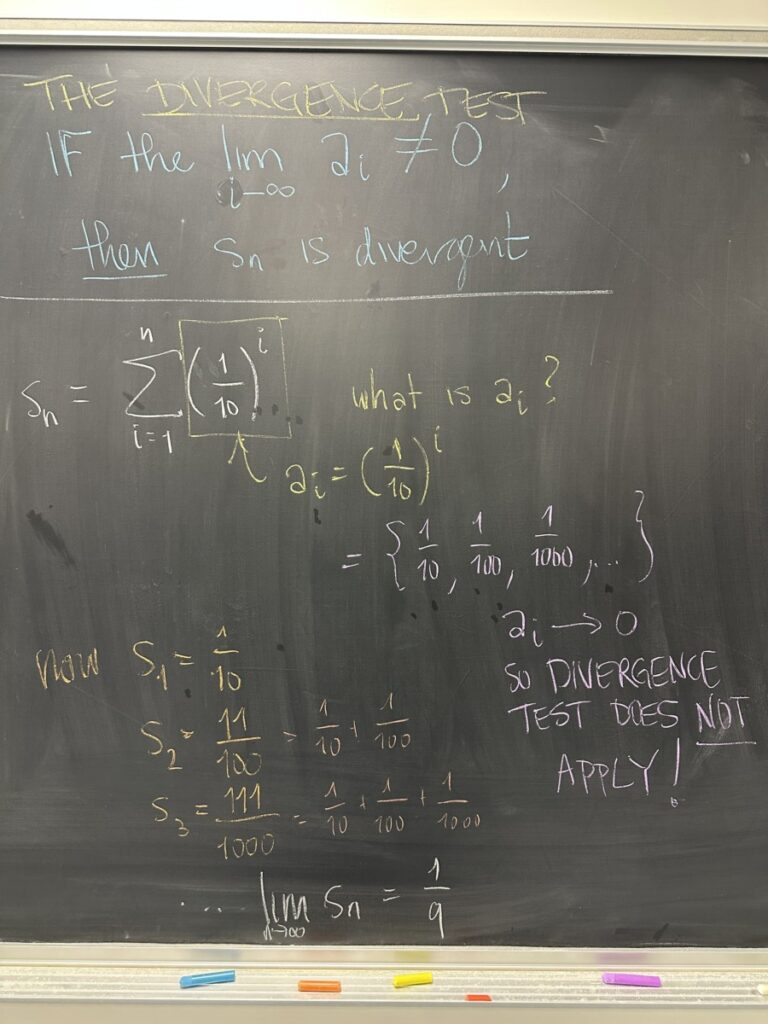
Usually, however, we will NOT know whether a series converges or diverges. So that last conclusion is pretty useless until we consider its contrapositive.
If a SEQUENCE has NON-ZERO limit, then its SERIES is DIVERGENT (cannot converge!). This is called the “divergence test” — we will learn lots of tests over the next several weeks, and it will be important to learn all their names!
We then looked at a specific series, one built from a geometric sequence.
First we identified the sequence, and we checked to see if the divergence test applied. Because the sequence had limit zero, we could not draw a conclusion.
Next we began looking at the sequence of partial sums. We noticed that there was a pattern: \(\{ 0.1, 0.11, 0.111, 0.1111, \ldots \} \) and that this sequence of partial sums (the SERIES) must converge to \(\dfrac{1}{9}\).
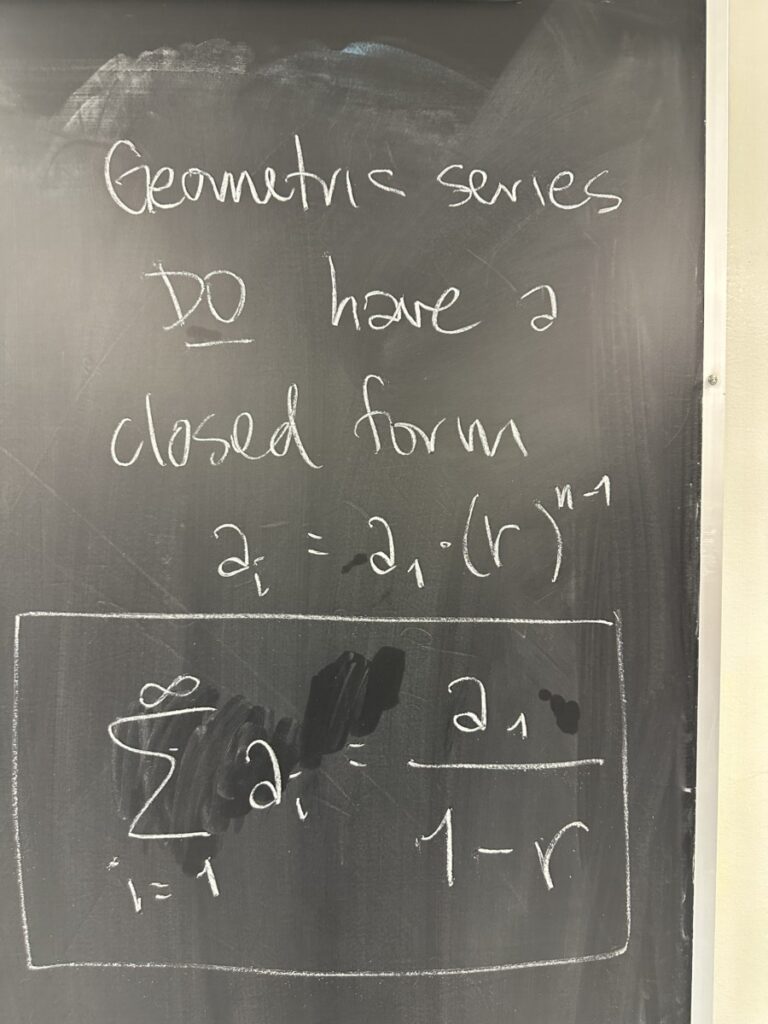
Geometric series are one of the few series where we WILL have a closed form for the sequence of partial sums.
\[s_n = a_1\left(\dfrac{1-r^n}{1-r}\right)\]
And the limit of this closed form will exist, so long as the common ratio, \(r\), has absolute value less than 1: \(|r| < 1\)
In such cases, \( \displaystyle \lim_{n\to\infty} r^n = 0 \), so
\(\displaystyle \lim_{n\to\infty} a_1\left(\dfrac{1-r^n}{1-r}\right) = a_1 \left( \dfrac{1-0}{1-r} \right) = \dfrac{a_1}{1-r}\)



Recent Comments