
Today’s quiz focused on the Limit Comparison Test from last week.
The first step one should always take when considering an infinite series is the foundational sequence \(a_i\). We are talking here about the values that will be added together in the infinite series.
In our second step, we consider the limit of the terms. (According to the Divergence Test, the limit of the \(a_i\) terms MUST be zero if there’s any chance of the infinite series converging.) In this case the limit of our \(a_i\) terms is indeed zero.
So, there’s a chance that our infinite series will converge… but how to proceed? Well, in the third step we identify that there is a p-series that is “close” to the one we were given. Construct a (different sequence) \(b_i\) that will approximate the one we started with. Use the relative powers or over-simplification to find \(b_i = \frac{1}{i}\) in this case.
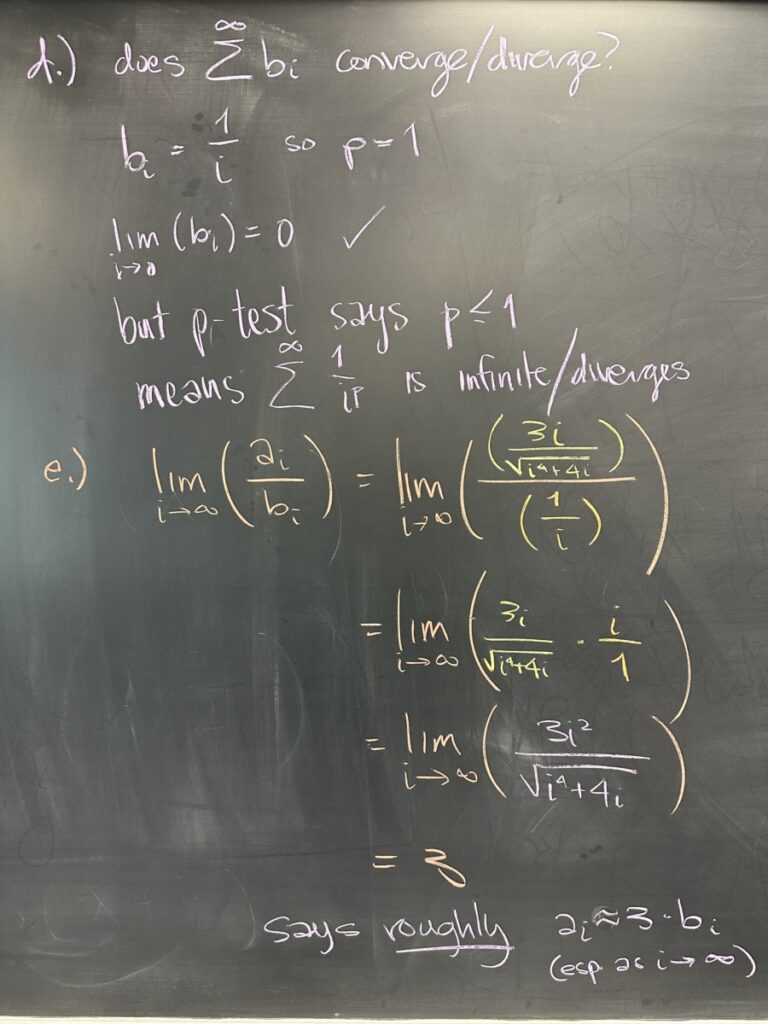
With our simplified p-series in hand, we consider whether or not the simplified series converges or diverges. Because it is a p-series, we know that \(p \geq 1\) (since \(p\) is \(1\)), and therefore the series \(\displaystyle\sum_{i=1}^{\infty} b_i\) diverges.
Because the sequences are have similar behavior, we expect the series to have similar behavior as well. But first we must show that the sequences have similar behavior!
In part “e” we show the similar behavior of the sequences by the fact that the limit of \(\dfrac{a_i}{b_i}\) is a non-zero constant. The meaning of this result is that since \(\dfrac{a_i}{b_i} \approx 3\) when \(i\) is very large (approaching \(\infty\)), we can say that \(a_i \approx 3 \cdot b_i\) when \(i\) is very large.
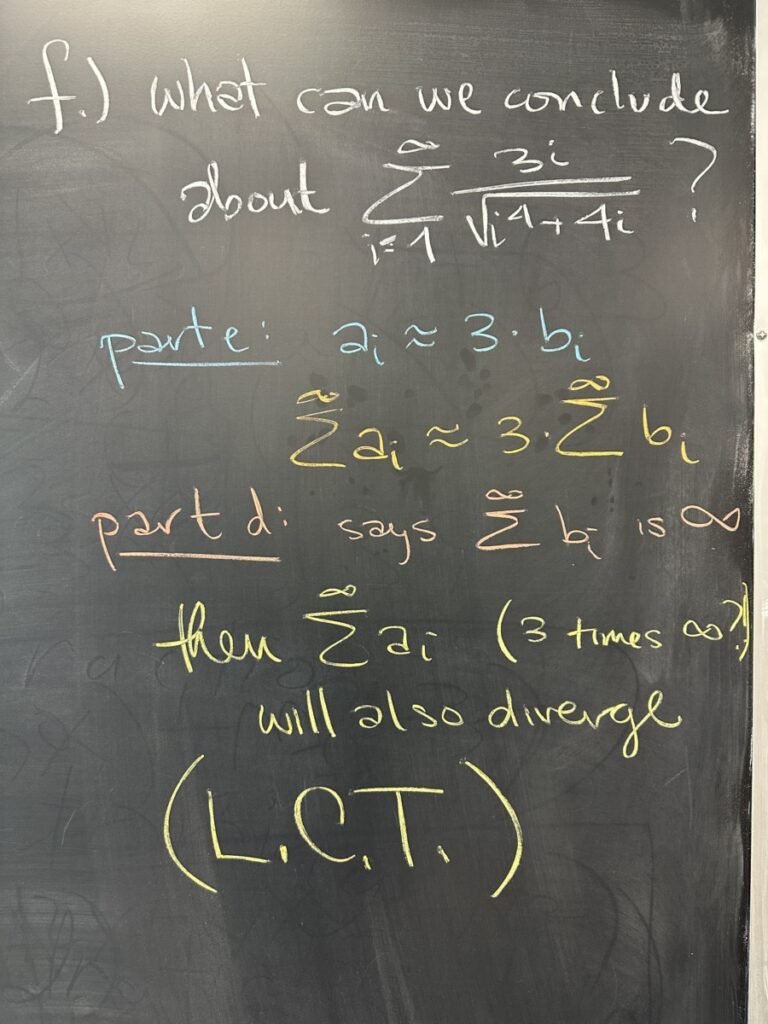
The Limit Comparison Test (L.C.T.) allows us to conclude that because the limit of \(\dfrac{a_i}{b_i}\) is a non-zero constant AND \(\displaystyle\sum^{\infty} b_i\) diverges, that then \(\displaystyle\sum^\infty a_i\) is also divergent.
Roughly speaking, since \(a_i \approx 3 \cdot b_i\) (at least for the infinite tail of the series), \(\displaystyle \sum^\infty a_i \approx 3 \cdot \sum^\infty b_i\). And because \(\displaystyle \sum^\infty b_i\) is infinite (divergent), then \(\displaystyle \sum^\infty a_i\) is also divergent.
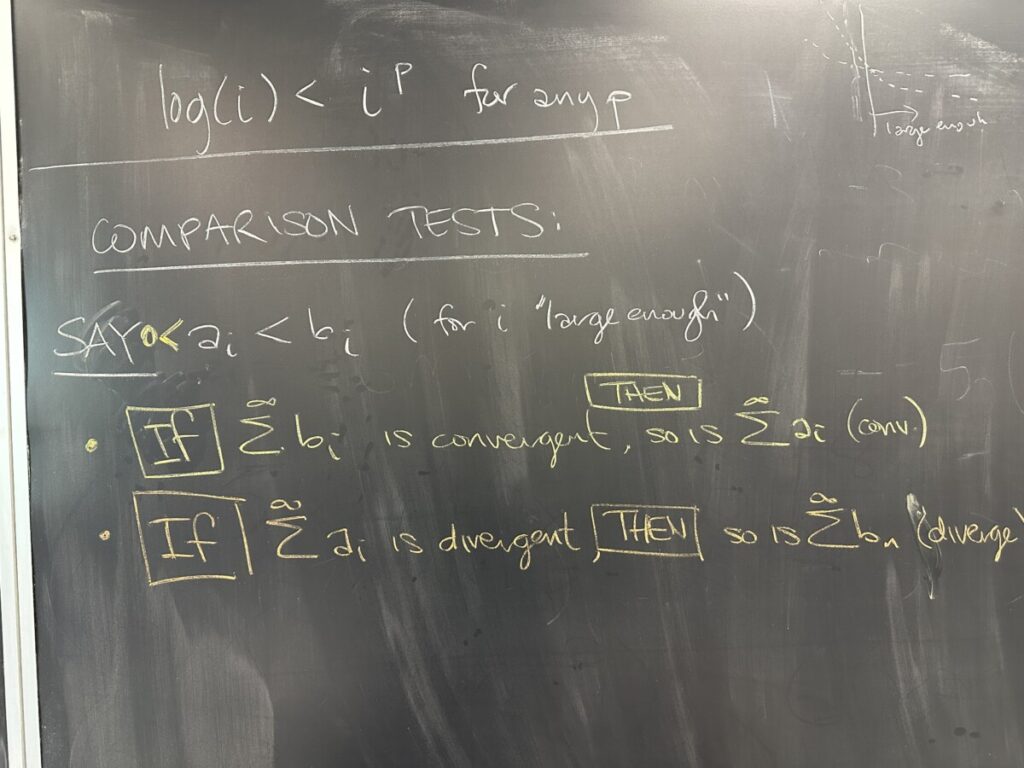
A question was then raised about \(\log(i)\) appearing in sequences. The answer to this question is more difficult than the L.C.T. allows for. Instead, we will use the comparison test (no limit is used here, only inequalities) for these sequences.
Logarithmic functions grow slower than any \(i^p\) function. Specifically, we mean the “slow” growing \(i^p\) functions where \(0 < p < 1\). For example \(\sqrt{i}\) or any \(\sqrt[n]{i}\).
If the larger series converges, the smaller series is bounded — since the sum of smaller terms cannot exceed the sum of the larger terms. The smaller series is also the limit of a monotone sequence (the sequence of partial sums is strictly increasing because we are only considering sums of positive terms — and adding a positive term MUST increase the sum). As a result, the smaller series must converge as the partial sums are monotone and bounded.
On the other hand, if the smaller series diverges, then it must be the case that it is unbounded (again, since partial sums of positive sequences must be monotone increasing). When we consider the larger series, then, we can only conclude that the sum must be larger than the sum of the smaller series, which we already know to be unbounded/infinite. Being larger than something unbounded forces the larger series to also be unbounded, hence divergent.

But today we wanted to (finally) get to some infinite series that include both positive and negative values!
We begin by considering sequences that have a very strict pattern of positive and negative values — the “alternating” sequences. These sequences may start with either a positive or negative value, but after that they must strictly alternate between positive and negative. Because of this requirement, every alternating sequence, \(a_i\) can be written as a power of negative-one (either \((-1)^i\) or \((-1)^{i+1}\)) times a strictly positive sequence (which we call \(b_i\)).
Alternating sequences can only converge to zero. (Otherwise, they do not converge at all, and therefore we would conclude that the infinite sum will diverge by the Divergence Test.) Furthermore, if \(a_i\) converges to zero, then so must \(b_i\).
So, if we have an alternating sequence \(a_i = (-1)^i \cdot b_i\) with \(\displaystyle\lim_{i\to\infty} a_i = 0 = \lim_{i\to\infty} b_i\), then the Alternating Series Test says that IF \(b_i\) is monotone (decreasing), THEN the series for \(a_i\), \(\displaystyle\sum^\infty (-1)^i b_i\) is convergent.
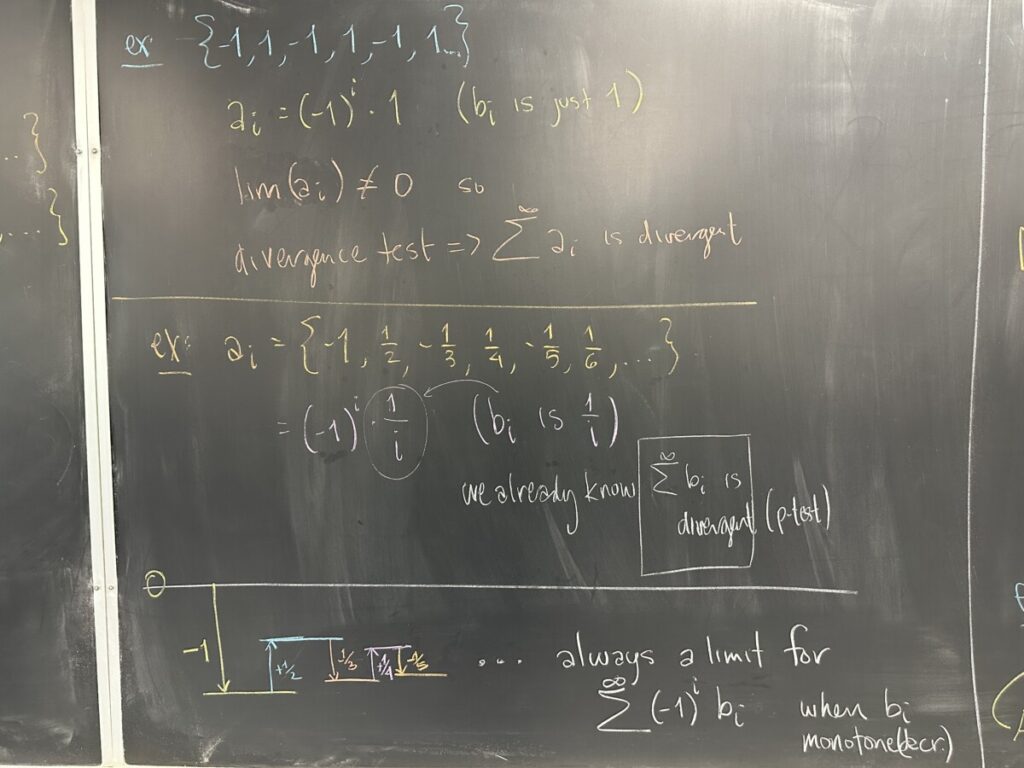
First, an example of an alternating sequence that does not have limit zero. The sequence of partial sums cannot converge either.
Then an example of an alternating series that does converge. Because the values being alternately added and subtracted are shrinking in value, we find our sum being continually “squeezed” in (as shown). We start at zero, then subtract 1 to land at -1. When we then add the next term, it will get us back towards zero, but since the next term has value \(\frac{1}{2}\) (less than 1, the previous term) we cannot reach back to zero. Then with the subtraction of the next term \(\frac{1}{3}\), it has value less than the previous \(\frac{1}{2}\), meaning we cannot go past the -1 which was our previous “lowest” value. As this process continues, we find that we can never go higher or lower than our previous values — as a result, we are forced to approach a limit.
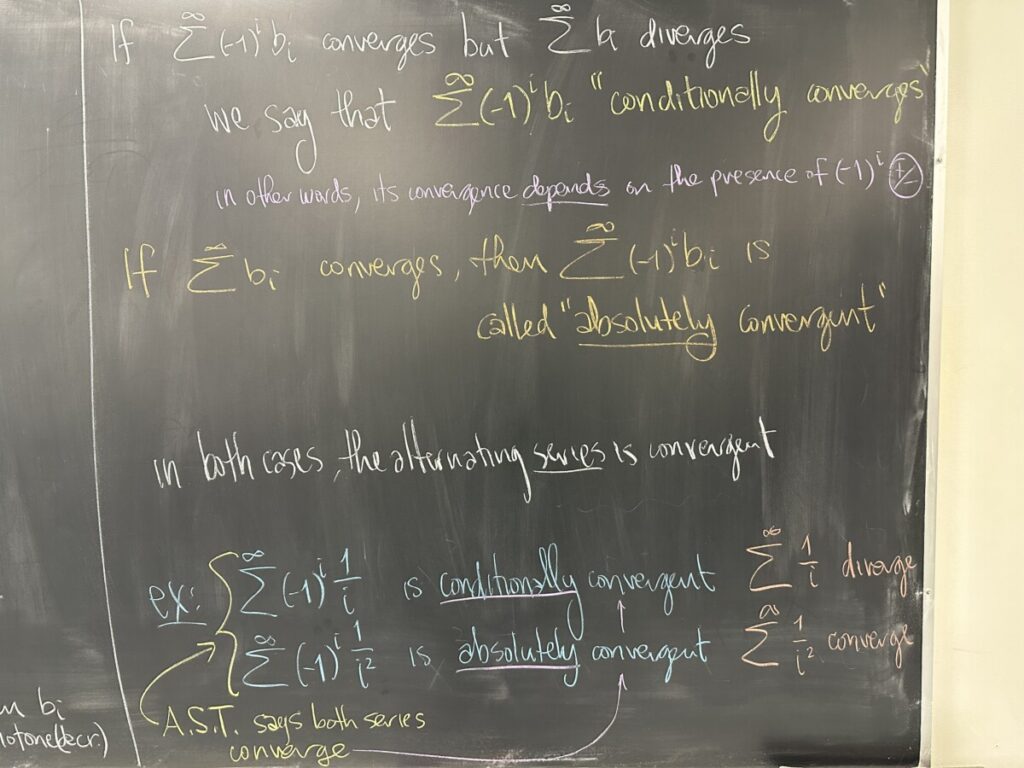
When an alternating series converges, we have a further classification that we can make depending on whether or not the series converges without the “alternating part”. In other words, depending on whether or not \(\displaystyle\sum^\infty b_i\) converges or diverges.
The presence of the alternating sign in the series \(\displaystyle\sum^\infty a_i\) means that half of the terms will be effectively subtracted (adding a negative value). Conceptually, it is a lot “easier” to avoid having an infinite limit when half the terms are subtracted in this way. So, there are going to be some convergent alternating series in both categories: \(\displaystyle\sum^\infty b_i\) convergent and \(\displaystyle\sum^\infty b_i\) divergent.
When both \(\displaystyle\sum^\infty a_i = \sum^\infty (-1)^i b_i\) and \(\displaystyle\sum^\infty b_i\) converge, we say that \(\displaystyle\sum^\infty a_i\) is “absolutely convergent”.
When only \(\displaystyle\sum^\infty a_i = \sum^\infty (-1)^i b_i\) converges (meaning \(\displaystyle\sum^\infty b_i\) diverges), we say that \(\displaystyle\sum^\infty a_i\) is “conditionally convergent”. In other words, the alternating series only converges because half the terms are subtracted.




Recent Comments