Ratio Test

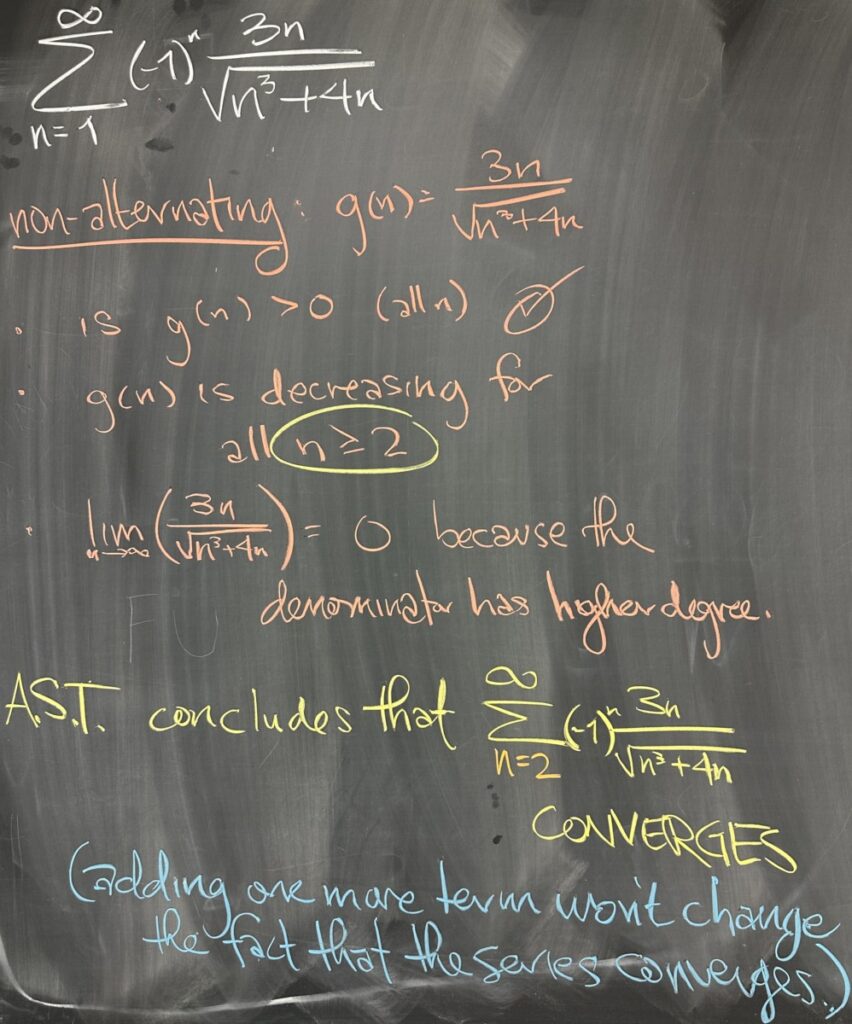
Today’s quiz was all about an alternating series: \[\sum^\infty_{n=1}(-1)^n\frac{3n}{\sqrt{n^3+4n}}\]

The first question asked everyone to use the Alternating Series Test to show that this series converges. There are three things that are necessary in order to apply the AST — and they all focus on the non-alternating portion of the sequence: \(f(n)=(-1)^n\frac{3n}{\sqrt{n^3+4n}}\)

The non-alternating version of the sequence is the result of treating any alternating factor (in this case\((-1)^n\)) as always being positive one. So for this problem, our non-alternating portion is \(g(n)=\frac{3n}{\sqrt{n^3+4n}}\). So what are the three parts of this test?

• Is \(g(n)>0\)? Since \(3n\), \(n^3\), and \(4n\) are all positive, \(g(n)\) is positive for all \(n\).i
• Is \(g(n)\) decreasing? Looking at the graph (or values \(g(1), g(2), g(3),\) etc.) of \(g(x)=\frac{3x}{\sqrt{x^3+4x}}\), we see that \(g(n)\) is isn’t decreasing from \(g(1)\) to \(g(2)\), but does decrease from \(n=2\) onwards. (This will not ultimately affect the overall application of the AST.)
• Finally, what is the limit: \(\displaystyle\lim_{n\to\infty} g(n)\)? Since the degree of \(g(n)\)’s denominator, \(\frac32\), is larger than the degree of the numerator, \(1\), this limit must be zero.

Conclusion: the Alternating Series Test applies, and proves that this series, \(\displaystyle\sum^\infty_{n=1}(-1)^n\frac{3n}{\sqrt{n^3+4n}}\) , converges.

The second part of the quiz asked about the convergence of \(\displaystyle\sum^\infty_{n=1}(-1)^n\frac{3n}{\sqrt{n^3+4n}}\). If you’re paying close attention, this is the “absolute” series for part a, \(\sum g(n)\). But does it converge or diverge?

We already know that \(g(n)\) is positive — so it’s eligible for the Limit Comparison Test. Since we have (roughly) only polynomial terms, we know that we should compare with a p-series, choosing \(p\) to be the difference between the degrees of the denominator (\(\frac32\)) and numerator (\(1\)). So we choose \(b_n=\frac{1}{\sqrt{n}}\), \(p=\frac12\).

We may be tempted to jump right into an analysis of the p-series \(\sum\frac{1}{\sqrt{n}}\), but whenever we attempt the Limit Comparison Test, it is important to first determine that the two series should have the same behavior before we spend the time analyzing \(\sum b_n\).

In order to draw conclusions with the Limit Comparison Test, we must determine that \(\displaystyle\lim_{n\to\infty} \frac{a_n}{b_n}\) is a finite, non-zero number. Since \(a_n=\frac{3n}{\sqrt{n^3+4n}}\) and \(b_n=\frac{1}{\sqrt{n}}\), the fraction can be simplified as follows: \[\frac{a_n}{b_n}=\frac{3n}{\sqrt{n^3+4n}}\frac{\sqrt{n}}{1}=\frac{3n^{\frac32}}{\sqrt{n^3+4n}}\]

This (roughly) rational function has equal degrees in the numerator and denominator (both \(\frac32\)), meaning that we get a horizontal asymptote (\(y=\frac31\)), and hence a limit \(\displaystyle\lim_{n\to\infty}\frac{a_n}{b_n}=3\). This limit is indeed a finite, non-zero number, so the Limit Comparison Test allows us to conclude that \(\sum a_n\) and \(\sum b_n\) either both converge OR both diverge together. (In other words, the Limit Comparison Test is telling us that it is impossible for one series to converge while the other diverges.)

Now is the time that we can proceed with the p-series Test — since LCT already confirmed that whatever the p-series does (either converge or diverge), \(\displaystyle \sum^\infty_{n=1}(-1)^n\frac{3n}{\sqrt{n^3+4n}}\) must also do.

Our p-series, \(\sum\frac{1}{\sqrt{n}}\), has \(p=\frac12\), which is less than one. Therefore, we conclude that this p-series diverges. Since \(\sum\frac{1}{\sqrt{n}}\) diverges, so must \(\sum(-1)^n\frac{3n}{\sqrt{n^3+4n}}\) also diverge.

Since \(\sum(-1)^ng(n)\) converges, but \(\sum g(n)\) does not, we conclude that the alternating series \(\sum(-1)^n\frac{3n}{\sqrt{n^3+4n}}\) is conditionally convergent. In other words, the convergence of the alternating series is dependent (“conditional”) on the fact that we end up subtracting half of the terms of the series.

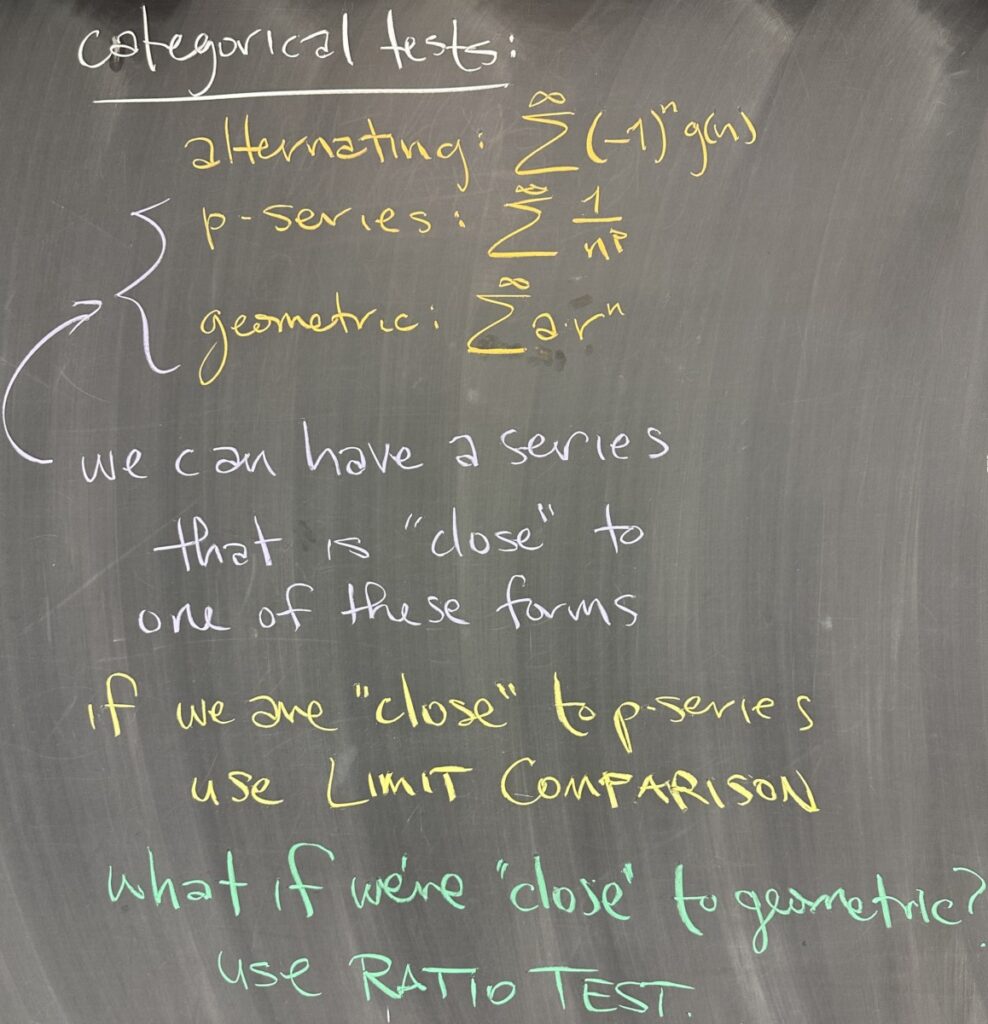
Before moving on to today’s lecture, I reminded everyone of the importance of knowing all of the series tests for Tuesday’s exam. It is essential that you are able to identify the “compute”, “compare”, and “conclude” portions of each of the tests that we have learned: Divergence Test, Geometric Series Test, p-series Test, Alternating Series Test, Direct Comparison Test, and the Limit Comparison Test. (The Ratio Test will not appear on the first exam.)

Three of these tests are “categorical” tests (they only apply to series that have a particular form). The Alternating Series Test only applies to series that have an alternating factor, such as: \((-1)^n, (-1)^{n\pm1},\) or \(\cos(\pi n)\). The Geometric Series Test only applies to series that have sequences with closed form \(f(n)=a(r)^n\). And p-series Test only applies to series that have sequences with closed form \(f(n)=\frac{1}{n^p}\).

In the case of p-series, if we have an \(a_n\) that is a (roughly) rational function (with degrees for the numerator and denominator), then we have the Limit Comparison Test that allows us to tie our \(\sum a_n\) to a p-series. We just saw an example of this from part b of the quiz.

But what if we have a series that is “close” to being geometric (instead of being “close” to a p-series)? We will see an example of a series that is “close” to being geometric in the next slide. In these cases, we have the Ratio Test to help us out.

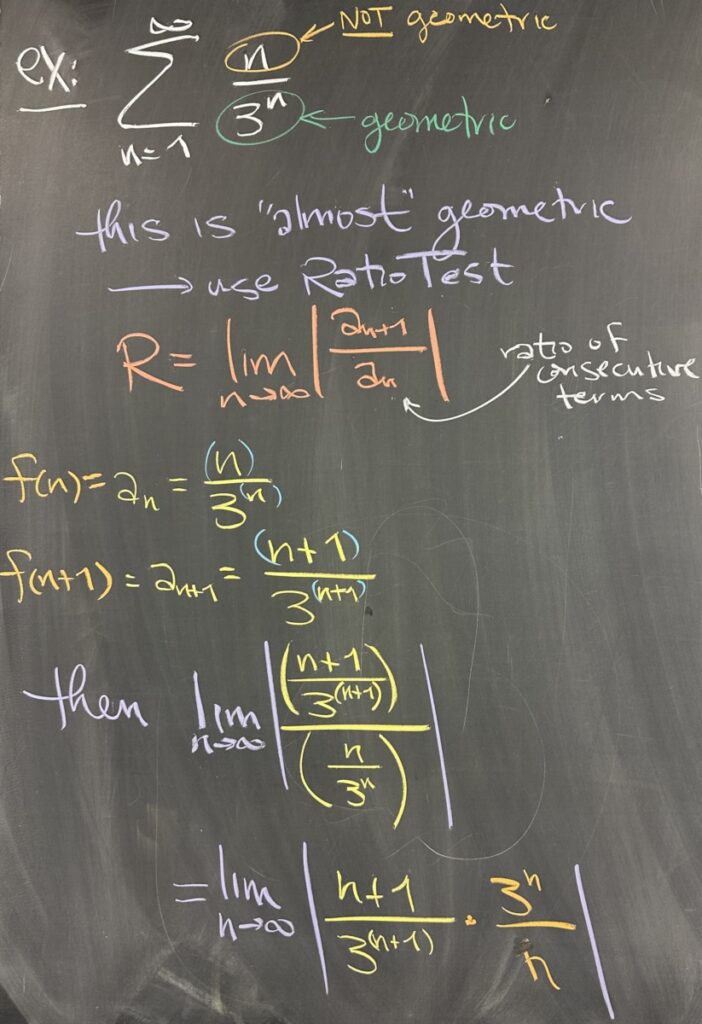
In this example, our sequence has closed form \(f(n)=\frac{n}{3^n}\). The denominator suggests geometric series (with \(n\) in the exponent), but the numerator is more in line what we would expect from a p-series. If we look at \(f(1), f(2), f(3)\), and so on, we will see that there is no common ratio — hence this cannot be a geometric series.

But it is “close” (we have some geometric pieces here!), so we will use the Ratio Test.

With geometric series, the common ratio is constant: \(r=\frac{a_{n+1}}{a_n}\). Since this series is not geometric, we instead consider how this ratio behaves as \(n\to\infty\): \[R=\lim_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|\]

This is a tricky spot, as I’ve seen it trip up a lot of students over the years. Take your time to carefully consider both \(f(n)\) and \(f(n+1)\).

• \(f(n)=\frac{n}{3^n}\)
• \(f(n+1)=\frac{n+1}{3^{n+1}}\)

Then consider the limit of the ratio \(\frac{f(n+1)}{f(n)}\): \[\lim_{n\to\infty}\left|\frac{f(n+1)}{f(n)}\right|=\lim_{n\to\infty}\left|\frac{\frac{n+1}{3^{n+1}}}{\frac{n}{3^n}}\right|=\lim_{n\to\infty}\left|\frac{(n+1)}{3^{n+1}}\cdot\frac{3^n}{n}\right|\]

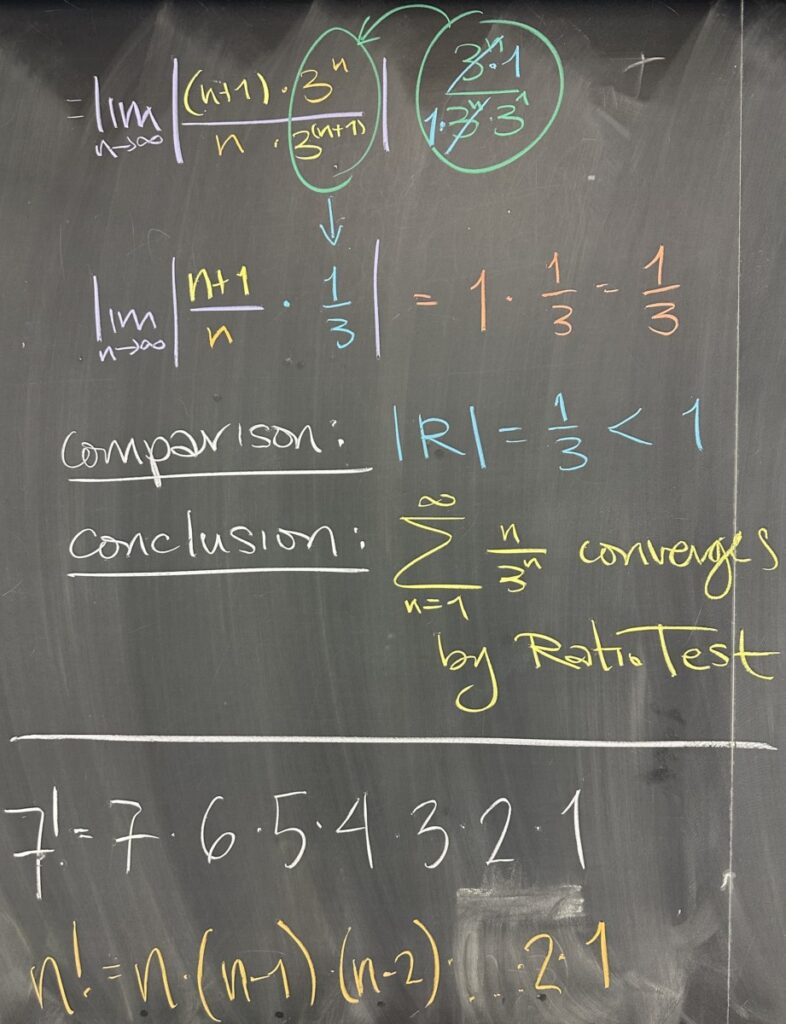
When working with these limits, it will be easier if we align similar factors: \[\lim_{n\to\infty}\left|\frac{(n+1)\cdot3^n}{3^{n+1}\cdot n}\right|=\lim_{n\to\infty}\left|\frac{(n+1)\cdot3^n}{n3^{n+1}}\right|=\lim_{n\to\infty}\left|\frac{n+1}{n}\frac{3^n}{3^{n+1}}\right|=\lim_{n\to\infty}\left|\frac{n+1}{n}\frac{3^n}{3^n\cdot1}\right|=\lim_{n\to\infty}\left|\frac{n+1}{n}\frac{1}{3}\right|=\frac13\]

The Ratio Test works very similarly to the Geometric Series Test, if \(|R|<1\), the series converges. (And, if \(|R|>1\), the series would diverge). Our \(R=\frac13\), so we conclude that \(\sum\frac{n}{3^n}\) converges by the Ratio Test.

We then move on to discuss the “factorial” operator. The factorial, \(n!\) is originally developed as the calculation of how many different ways \(n\) objects can be put in order. In the classroom, I happen to have 7 different colors of chalk — how many different ways can I put the different colors?

There are 7 options for the first color, but the options for the second color are fewer, since one color was already taken as the first option. So there are 6 options for the second, then 5 options for the third, and so on. So the total number of ways I can arrange the 7 colors is \(7!=7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1\).

In general, if \(n\) is unknown, we cannot say how long this product will be (so we must use “\(\ldots\)”): \(n!=n\cdot(n-1)\cdot(n-2)\ldots 2\cdot 1\).

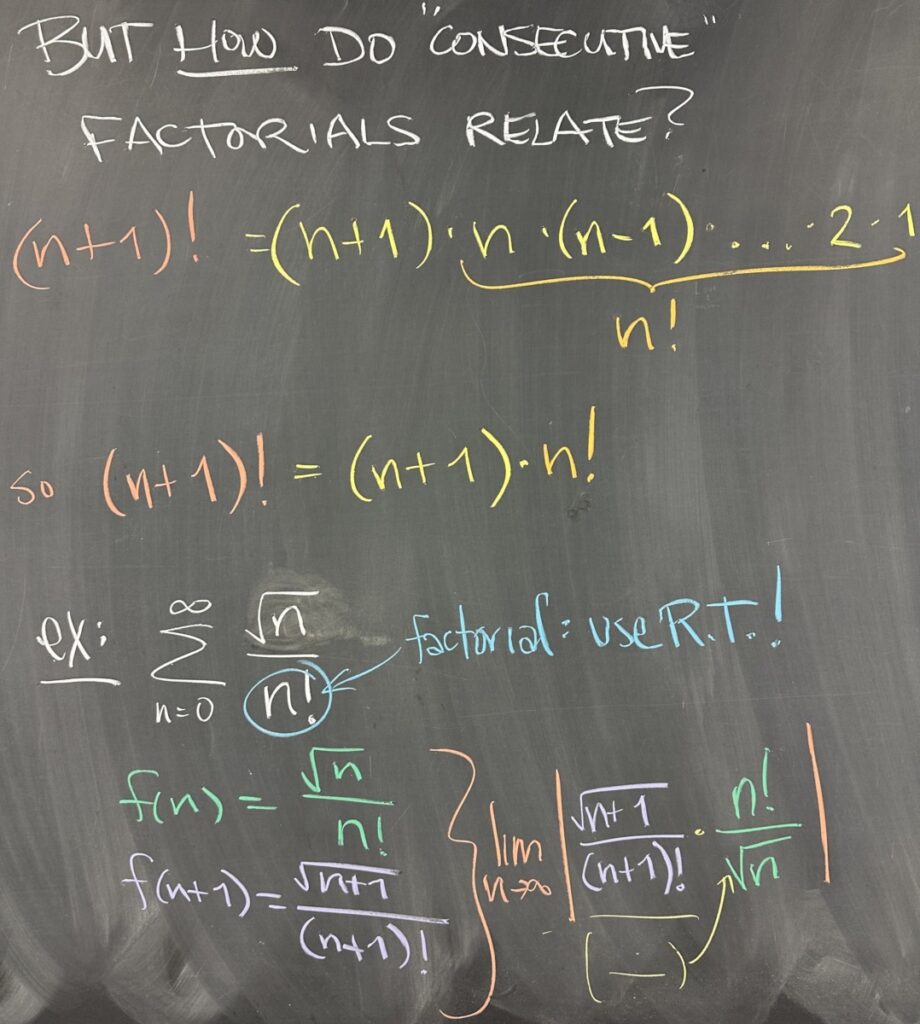
Because we’re looking to use the Ratio Test whenever a factorial is present, it will be important to understand how consecutive factorials relate. Think about how things change from \(7!\) to \(8!\). With \(8!\), there are 8 options for the first choice — but after that we are counting down from 7, just as we did for \(7!\). So \(8!\) is 8 times \(7!\), in other words \(8!=8\cdot 7!\).

In general, we can say that \((n+1)!=(n+1)n!\). This will come into play as we explore the next example: \(\sum\frac{\sqrt{n}}{n!}\).

Since we see a factorial, we will aim to use the Ratio Test, which means considering \(f(n)\) and \(f(n+1)\).

• \(f(n)=\frac{\sqrt{n}}{n!}\)
• \(f(n+1)=\frac{\sqrt{n+1}}{(n+1)!}\)
• Simplify the ratio: \(\frac{f(n+1)}{f(n)}=\frac{\frac{\sqrt{n+1}}{(n+1)!}}{\frac{\sqrt{n}}{n!}}=\frac{\sqrt{n+1}n!}{(n+1)!\sqrt{n}}\)

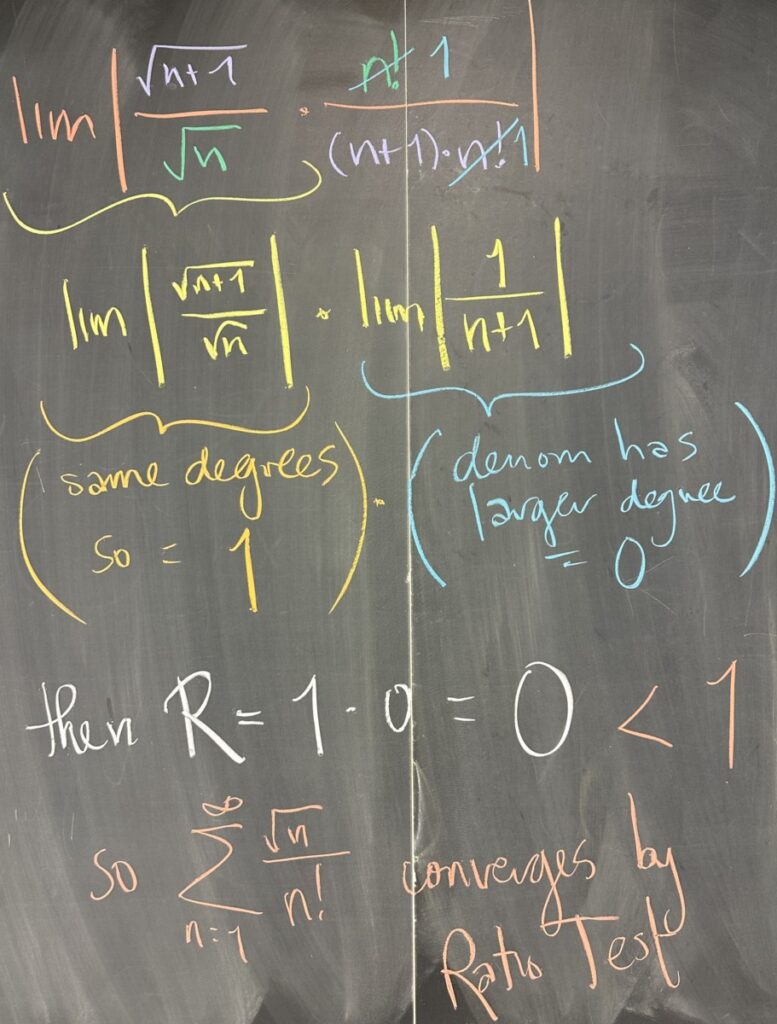
The “compute” task of the Ratio Test means that we must take the limit of the ratio we just simplified: \[\lim_{n\to\infty}\left|\frac{f(n+1)}{f(n)}\right|=\lim_{n\to\infty}\left|\frac{\sqrt{n+1}\cdot n!}{\sqrt{n}\cdot(n+1)!}\right|=\lim_{n\to\infty}\left|\frac{\sqrt{n+1}}{\sqrt{n}}\cdot\frac{n!}{(n+1)!}\right|\]

We may split this limit of a product into the product of two limits: \(\lim\frac{\sqrt{n+1}}{\sqrt{n}}=1\) and \(\lim\frac{n!}{(n+1)!}=\lim\frac{n!}{(n+1)\cdot n!}=\lim\frac{1}{n+1}=0\). So the limit of the product is \(1\cdot 0\). This is our \(|R|\) for the ratio test, and it is certainly less than one. We conclude that this series \(\sum\frac{\sqrt{n}}{n!}\) converges by the Ratio Test.